Resultats de la cerca
Es mostren 79 resultats
distributiu | distributiva
Matemàtiques
Dit d’una llei de composició interna quan satisfà determinades propietats.
En un conjunt E dotat de dues lleis de composició internes o operacions, una d’elles és distributiva respecte a l’altra quan se satisfan les següents propietats si a * b° c = a * b ° a * c hom diu que * és distributiva per l’esquerra respecte a °, si b° c* a = b * a ° c * a llavors, * és distributiva per la dreta respecte a °, i si se satisfan ambdues condicions hom diu que * és distributiva respecte a ° A ℝ, la multiplicació és distributiva respecte a la suma, però no a l’inrevés
polinomi
Matemàtiques
Suma formal de productes de nombres, anomenats coeficients (reals, complexos o, més generalment, elements de qualsevol anell) per elements anomenats variables (generalment denotats per x, y, z, etc), als quals hom atribueix només les propietats algèbriques més simples.
Usant aquestes propietats hom defineix la suma i el producte de polinomis, de manera que els polinomis de n variables formen una àlgebra Substituint les variables per nombres hom obté una funció anomenada funció polinòmica
topologia

Topologia Les figures unides amb fletxes són topològicament iguals, perquè és possilbe passar de l’una a l’altra per mitjà d’una transformació contínua
© Fototeca.cat
Matemàtiques
Part de la matemàtica que estudia aquelles propietats dels conjunts de punts de la recta, del pla, de l’espai o d’espais de dimensions superiors que no són alterades per les transformacions contínues.
Es tracta de propietats geomètriques que no depenen de cap magnitud, sinó únicament de la posició relativa dels punts Per exemple, el fet que dos punts puguin unir-se o no per un camí, o que el nombre de cares menys el d’arestes més el de vèrtexs d’un políedre esfèric sigui sempre dos teorema d’Euler Aquí hom entén per transformació contínua aquella que admet una inversa i que tant ella com la inversa són contínues L’íntima connexió que hi ha entre el concepte de continuïtat d’una funció en un punt i el d’entorn d’un punt permet de transportar l’estudi de propietats…
càlcul de diferències
Matemàtiques
Estudi de les propietats d’una funció de la qual hom només coneix un conjunt finit de valors f(x0), f(x1), ..., f(xn), que corresponen als arguments x0, x1, ..., xn, els quals, habitualment, són presos en progressió aritmètica xr=x0+rϖ.
Hom defineix l’ operador diferència Δ, mitjançant l’expressió Δf x = f x + ϖ - f x , i l’ operador incremental E , definit per E ϖ f x = f x + ϖ = f x + Δ f x , de manera que E = 1+Δ Les propietats d’aquests permeten d’assolir el resultat següent, dit teorema de Gregory f x + nϖ = E nϖ f x = 1+Δ n f x , on, en l’última expressió, hom pot emprar la fórmula del binomi de Newton Aquests operadors poden expressar les diferències dividides Hom pot obtenir una aproximació polinòmica a la funció f x amb la fórmula d’interpolació de Newton en la qual, si f x és n…
anàlisi harmònica
Matemàtiques
Representació de funcions periòdiques mitjançant sumació i integració de desenvolupaments en sèrie d’algunes funcions trigonomètriques elementals.
Permet d’obtenir expressions senzilles aproximades de les funcions i deduir propietats generals a partir de les propietats particulars d’aquelles funcions elementals
multiplicació
Matemàtiques
Operació aritmètica que, donats dos nombres naturals a (el multiplicand) i b (el multiplicador), consisteix a trobar un nombre, ab, a × b o a · b, que és el resultat de sumar b vegades el nombre a
.
En teoria de conjunts, hom defineix el nombre ab com el cardinal del producte cartesià A × B , on A és un conjunt de cardinal a , i B un conjunt de cardinal b La multiplicació és anomenada també producte i gaudeix de les propietats associativa, commutativa i distributiva respecte a la suma En les successives extensions del conjunt de nombres naturals fins a arribar als nombres complexos, hom va generalitzant convenientment la definició de la multiplicació, sense perdre, però, cap de les propietats anteriors ni tampoc la propietat que l’element neutre es pot anar…
hiperplà
Matemàtiques
Conjunt de punts d’un espai n-dimensional tals que llurs coordenades satisfan una equació lineal.
Els hiperplans tenen propietats algèbriques anàlogues a les dels plans en coordenades cartesianes
afinitat
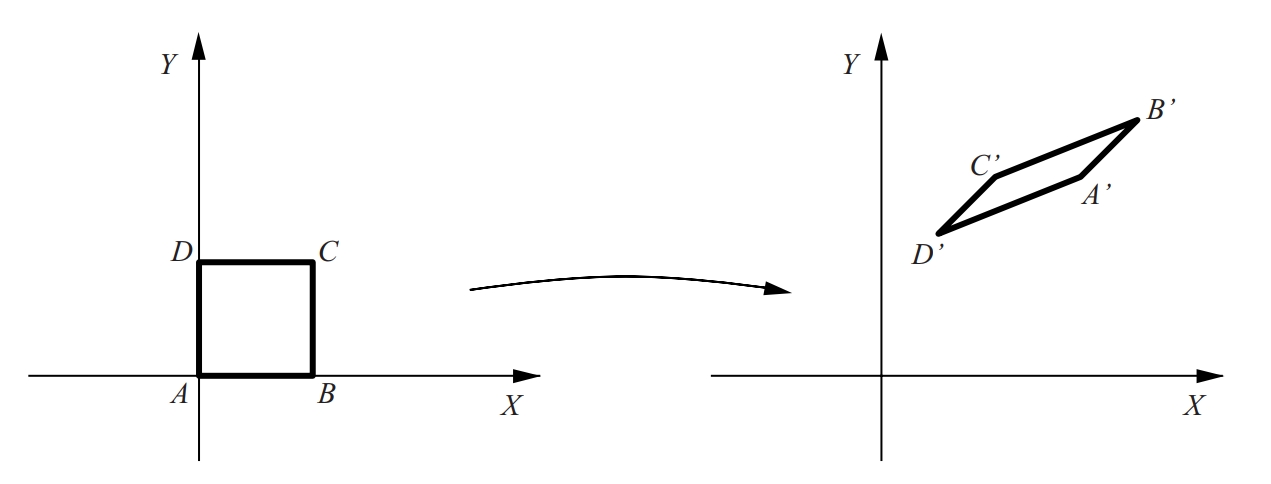
afinitat Transformació afí d’un quadrat
© Fototeca.cat
Matemàtiques
Transformació de l’espai afí en si mateix, que fa correspondre línies paral·leles amb línies paral·leles, punts propis amb punts propis i no canvia el subespai de l’infinit.
Enclou, entre d’altres transformacions, la traslació, la rotació i la simetria Les propietats geomètriques conservades per aquesta transformació són dites afins o lineals llur estudi constitueix la geometria afí
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- Pàgina següent
- Última pàgina