Resultats de la cerca
Es mostren 14 resultats
Pappus d’Alexandria
Matemàtiques
Matemàtic grec.
És autor d’una Collecció matemàtica en vuit volums, d’un gran valor, tant per la immensa documentació aportada com per l’extensa recopilació que suposa dels treballs anteriors d’altres matemàtics Enuncià, a més, alguns teoremes geomètrics propis, com el teorema del centroide teoremes de Guldin i el teorema de l’hexàgon
ajust
Matemàtiques
Operació estadística que consisteix a trobar la llei que resumeix, de la millor manera possible, la variació d’una variable aleatòria Y
en funció d’una altra variable X
, de la qual depèn.
Hom fa l’ajust a partir del coneixement de parells de valors x,y obtinguts observant una mostra, com la capacitat pulmonar i l’edat Deixant de banda l’ajust purament gràfic allisatge, habitualment hom pren una funció f x lineal, exponencial, polinòmica, etc i se suposa que y=f x +ε, on ε és un residu aleatori o soroll, i els paràmetres que defineixen la funció són determinats pel mètode dels mínims quadrats
Èudox de Cnidos
Astronomia
Filosofia
Matemàtiques
Matemàtic, metge, astrònom i filòsof grec.
Estudià matemàtiques amb Arquites a Tàrent, medicina amb Filistió Sicília, astronomia a Heliòpolis Egipte i filosofia a l’escola de Plató d’Atenes Féu observacions astronòmiques a Heliòpolis 381 aC, i més tard es dedicà a l’ensenyament a Atenes 365 aC Desenvolupà la teoria planetària de Plató i suposà que cada planeta es mou sobre una esfera, totes concèntriques, amb una Terra esfèrica al centre Establí un mapa d’estels i dividí l’esfera celeste en graus de longitud i latitud Establí la durada de l’any en 365 dies i 6 hores, i creà un mètode per a mesurar àrees Desenvolupà una…
permutació
Matemàtiques
Aplicació d’un conjunt de n elements a n llocs diferents, és a dir, cadascun dels diferents arranjaments lineals que es poden fer amb diferents elements, entrant tots ells en cadascun dels arranjaments.
El nombre de permutacions diferents que hom pot fer amb un conjunt de n elements és n n factorial i és donat per la fórmula n = n n- 1 n -2 2 × 1 Si hom identifica alguns dels elements del conjunt, obté les permutacions amb repetició Si el conjunt és identificat en classes de n 1 , n 2 n r elements, el nombre de permutacions amb repetició és n / n 1 n 2 n r Si hom suposa que els llocs són disposats en un cercle i que no es distingeix entre dues permutacions si només difereixen en una rotació, hom obté les permutacions circulars , tant amb repetició com sense Llur nombre, en tots…
regla de Simpson
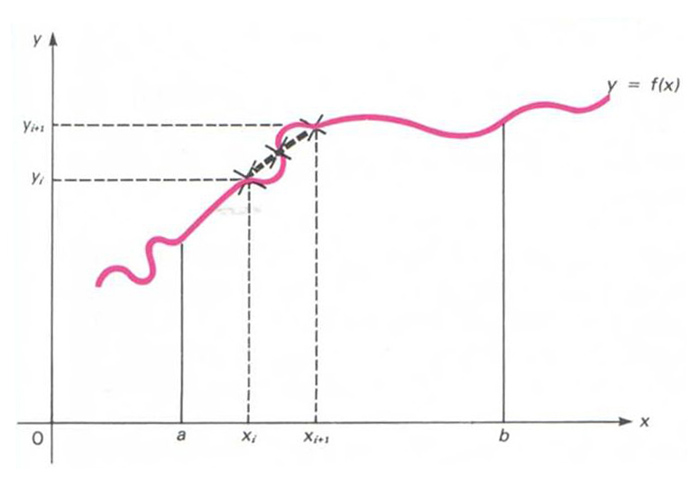
Regla de Simpson
© fototeca.cat
Matemàtiques
Mètode per a aproximar l’àrea limitada per una corba y = f(x), l’eix OX i dues rectes paral·leles x = a i x = b.
El mètode suposa que els petits arcs de la corba són aproximables mitjançant arcs de paràbola que passen pel punt mitjà i pels punts terminals de l’arc considerat La fórmula que hom obté amb aquesta aproximació és usant les sèries de Taylor fins als termes quadràtics on l’interval a,b ha estat dividit en 2 n subintervals a, x 1 , x 2 , , x 2 n - 1 , b , i y a , y 1 , y 2 , , y 2 n - 1 , y b són les respectives ordenades d’aquests punts, y i = f x i La diferència numèrica entre l’àrea real i aquesta àrea aproximativa A , és fitada per la quantitat M b-a 5 /1802 n 2 , on M és el…
allisatge
Matemàtiques
Conjunt de mètodes per al tractament de dades estadístiques de tipus cronològic o sèries temporals, que tenen per objecte fer previsions a curt termini basades en les dades anteriors.
Hom tracta de separar la fluctuació aleatòria de la llei subjacent del fenomen, allisant els valors històrics anteriors La més emprada és la tècnica anomenada de les mitjanes mòbils , que pren com a previsió la mitjana aritmètica de les N darreres dades Hom pot veure fàcilment que S t +1 = S t + X t — X t-N /N Si es tracta, p ex, de preveure les vendes d’un producte per al més següent t+ 1, hom pren la mitjana dels darrers dotze mesos, amb la qual cosa hom suposa que s’eliminaran les variacions aleatòries El mètode de l' allisatge exponencial representa una elaboració de l’anterior que…
arbre
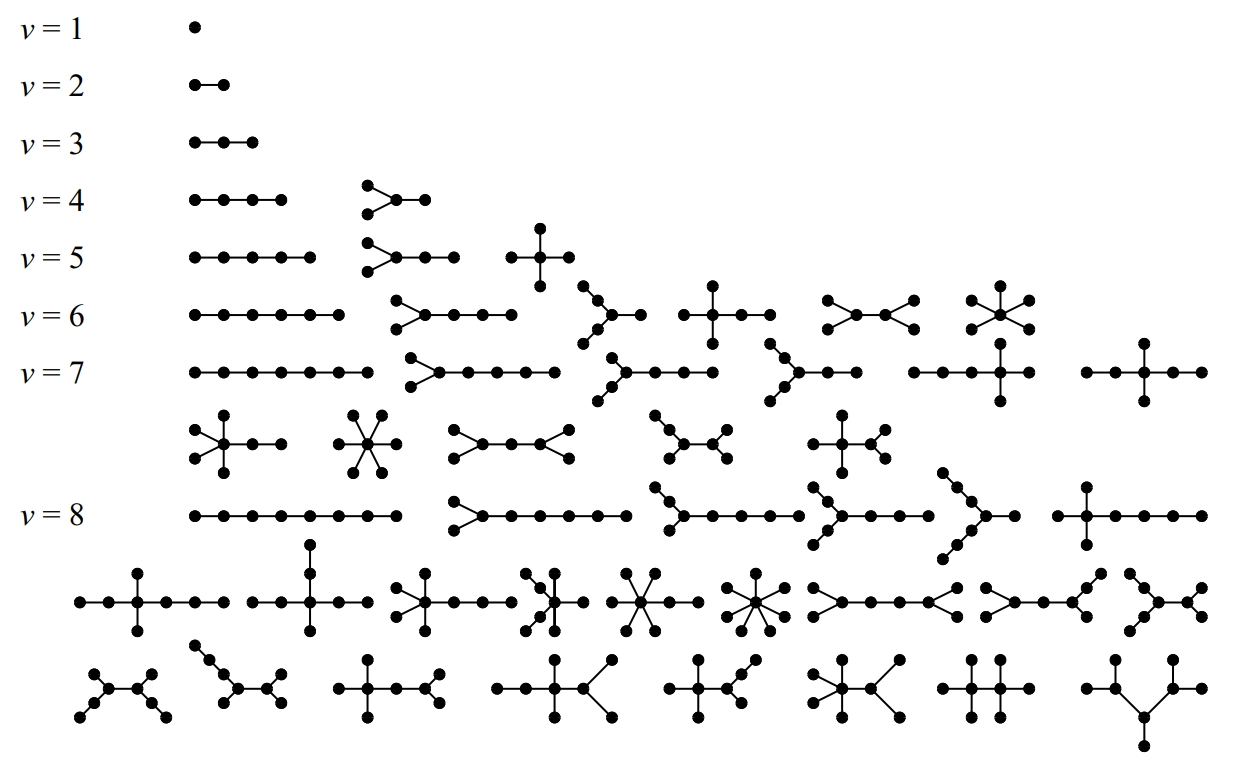
Tots els arbres amb vuit vèrtexs com a màxim
© fototeca.cat
Matemàtiques
Graf connex i acíclic (sense circuits).
Un arbre té només un vèrtex, anomenat arrel sense predecessor en el sentit de les fletxes, mentre que tot altre vèrtex té, cada un, un únic predecessor Tots els vèrtexs tenen un nombre variable de successors, que ordinariàment hom suposa ordenats per exemple, d’esquerra a dreta i de vegades són anomenats branques En la representació habitual d’un arbre l’arrel se situa al capdamunt i els arcs se suposen recorreguts en sentit descendent Els arbres han passat d’ésser un cas particular de graf a rebre un tractament matemàtic específic Són particularment útils en la modelització de processos en…
perspectiva cònica
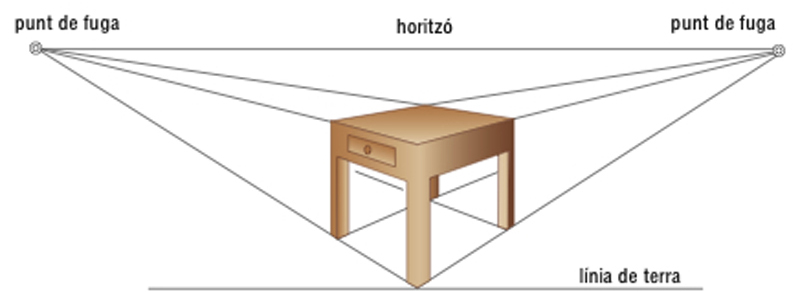
Representació d’una taula en perspectiva cònica obliqua (dos punts de fuga)
© Fototeca.cat
Art
Disseny i arts gràfiques
Matemàtiques
Perspectiva central el centre de projecció o pol de la qual és l’ull de l’observador.
Per al traçat d’aquesta perspectiva, hom admet que la llum que arriba a l’ull procedent de qualsevol punt d’un objecte és una línia recta, que rep el nom de raig visual Els principals elements per al seu traçat són la posició de l’ull o punt de vista , de la qual depèn l’efecte de la perspectiva l' horitzó o la línia horitzontal traçada en el pla del quadre, a l’alçada del punt de vista, que ocupa en el quadre la mateixa posició que la perspectiva de l’horitzó natural el pla geometral , que és el pla perpendicular al pla del quadre i on hom suposa que són situats l’observador i els objectes…
nombre real
Matemàtiques
Cadascun dels nombres que hom pot obtenir en mesurar magnituds contínues.
Hom obté el conjunt dels nombres reals completant el conjunt dels nombres racionals amb tots els nombres irracionals que poden ésser representats sobre la recta, tals com etc La manera més simple d’introduir teòricament i d’utilitzar en la pràctica els nombres reals és per mitjà de llur expressió decimal Tot nombre real és expressat en forma decimal amb infinites xifres que, en el cas dels nombres irracionals, no es repeteixen periòdicament Això suposa que per a definir un nombre real cal donar una llei que permeti d’obtenir tantes xifres decimals com hom vulgui A la pràctica, però, hom pren…
problema
Matemàtiques
Tota qüestió en què partint d’unes dades conegudes cal arribar a uns resultats.
El resultat d’un problema pot ésser de natura molt diversa cal distingir, dins la matemàtica, els problemes de calcular, els problemes de construir i els problemes de demostrar En els problemes de calcular , és possible que per analogia amb altres problemes ja coneguts hom pugui aplicar unes regles que donen directament la solució, que pot constar d’un o més nombres Quan aquestes regles no són fàcils de descobrir hom recorre a expressar algèbricament les condicions de l’enunciat, és a dir, expressar per mitjà d’equacions les relacions entre les dades i les incògnites del problema si aquestes…