Resultats de la cerca
Es mostren 5 resultats
derivada parcial d’una funció en un punt
Matemàtiques
Donada una funció real, f:D⊂ℝn→ℝ, i un punt del seu domini de definició, a=(a1,...,an) ∈D, derivada en el punt ai de les funcions d’una variable fi(xi) = f(a1,...,xi,...,an)
.
La i-èsima derivada parcial de f en el punt a és, doncs, el nombre ∂ f/∂x i a = df i /dx i a i Si aquesta és, al seu torn, derivable, hom pot definir derivades parcials d’ordres superiors , com, per exemple, ∂ 2 f /∂ x i ∂x j = ∂∂ f / ∂x i / ∂ x j
moviment
Matemàtiques
Aplicació d’un espai mètric en ell mateix que conserva la distància.
Actualment hom tendeix a anomenar-lo isometria El conjunt de moviments definits sobre un espai, amb l’operació de composició o producte de moviments, constitueix un grup En particular, és interessant l’estudi dels moviments al pla i a l’espai ordinaris El grup dels moviments del pla és generat per les simetries axials, és a dir, tot moviment del pla pot ésser descompost en producte d’un cert nombre de simetries axials Els de nombre parell són anomenats moviments directes , conserven el sentit del pla i són un subgrup del grup de moviments els altres són anomenats moviments inversos Dins el…
derivada d’una funció en un punt
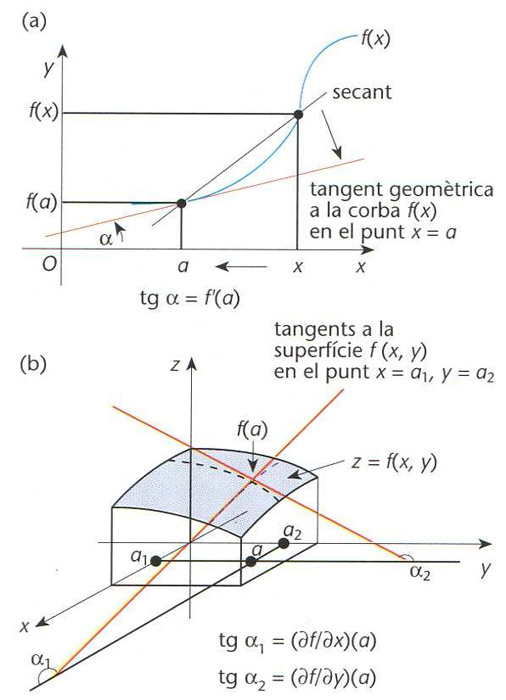
Interpretació gràfica de la derivada d’una funció (a) i de les derivades parcials d’una funció de dues variables (b); en (a), tgα = f' (a); en (b), tgα1 = ϑf/ϑx (a) i tgα2 = ϑf/ϑy (a)
© fototeca.cat
Matemàtiques
Donada una funció f: D⊂ℝ→ℝ i un punt del seu domini de definició, a ∈D, límit, si existeix del quocient [f(x) — f(a)]/(x-a) quan x tendeix a a tot mantenint-se a l’interior de D.
Quan aquest límit existeix, hom diu que la funció f és derivable en a , i el límit és notat per f´ a , df/dx a o Df a , i hom l’anomena derivada de f en el punt a Hom diu que f és derivable en un cert domini S si ho és a cada punt de S Aleshores, la funció f´ x que assigna a cada punt a ∈ S la derivada de f en a és anomenada funció derivada de f o, simplement, derivada de f Si f´ x és, al seu torn, derivable en un cert domini T , hom pot definir-n'hi la derivada, que és la derivada segona de f, f´´ x Hom procedeix consecutivament per tal de definir les derivades d’…
discontinuïtat
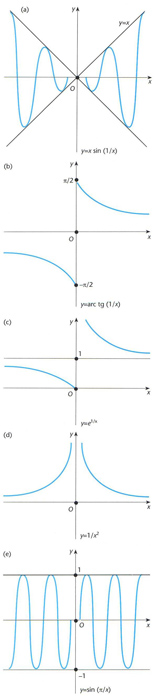
Discontinuïtat d’una funció: (a) discontinuitat evitable en x = 0, amb valor veritable y(0) = 0; (b) discontinuïtat de primera espècie infinita en x = 0, amb salt -2; (c) discontinuïtat de primera espècie infinita amb un punt d’infinit en x = 0; i (e) discontinuïtat de segona espècie finita en x = 0, per inexistència d’ambdós límits laterals quan x 0
© Fototeca.cat
Matemàtiques
Manca de continuïtat d’una funció en un punt o en un conjunt de punts, els quals són anomenats, per extensió, les discontinuïtats de la funció.
Atès que una funció f x és contínua en un punt a si i només si existeix i és igual a f a , la funció f x és discontínua en a si i només si no se satisfà alguna d’aquestes dues condicions, la qual cosa s’esdevé en els següents casos En primer lloc, pot passar que existeixi però que f a no existeixi f no sigui definida a a , o bé que aleshores, a és una discontinuïtat evitable , i la discontinuïtat és evitada redefinint el valor de f x al punt a tot assignant-li el valor el qual és anomenat valor veritable de f x en a En segon lloc, pot ocórrer que no existeixi aleshores, a és una…
entorn
Matemàtiques
En un espai topològic E, part de E que conté un obert de E que al seu torn conté un punt x o una part A de E; en el primer cas, hom parla d’entorn d’un punt, i, en el segon, d’entorn d’una part de E
.