Resultats de la cerca
Es mostren 51 resultats
horòscop
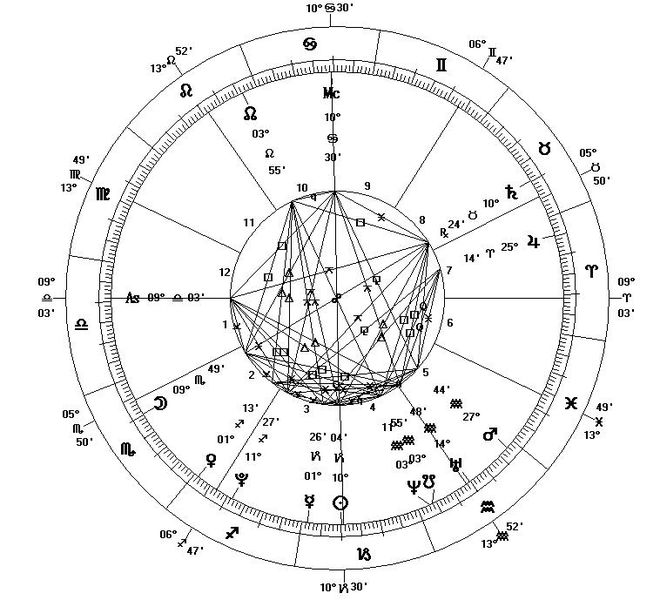
Horòscop calculat per l'1 de gener de 2000 a les 12 hores a Nova York
© Maksim
Esoterisme
Mapa celeste de la posició geocèntrica dels astres, en un moment determinat, que els astròlegs utilitzen per a fer llurs prediccions i judicis.
Generalment es refereix al moment del naixement d’una persona, però també pot referir-se a un animal, un objecte, un esdeveniment, un país, etc Consta d’una circumferència dividida en 360° sexagesimals, repartits en 12 sectors de 30°, a cadascun dels quals correspon un signe zodiacal , i hom hi indica les posicions planetàries en el moment estudiat i la corresponent divisió en cases segons la latitud i l’hora del dia en què tingué lloc l’esdeveniment Hom fa l’estudi astrològic de l’horòscop tenint en compte especialment la posició dels astres en els signes i les cases astrològiques i els…
teoremes de Guldin
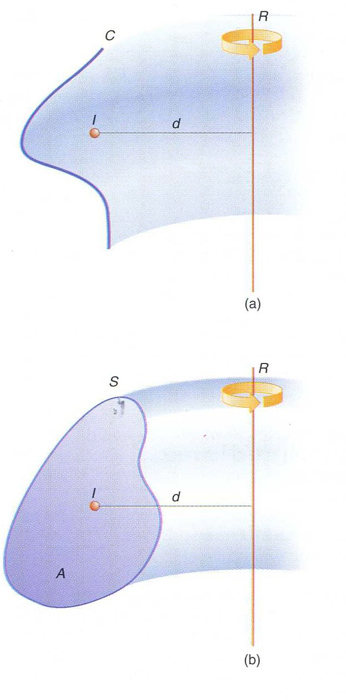
teoremes de Guldin: (a) primer teorema; (b) segon teorema
© fototeca.cat
Matemàtiques
Teoremes que relacionen el centre de massa d’una corba o d’una superfície amb l’àrea o el volum, respectivament, que generen en girar al voltant d’un eix.
Segons el primer teorema de Guldin , donada una corba plana C , de longitud l , que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2π dl , on d és la distància des del centre de massa I de la corba a la recta R en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material El segon teorema de Guldin afirma que, donada una superfície plana S , d’àrea A…
quocient assimilatori
Biologia
Relació que hom pot establir entre la quantitat de substàncies nutritives consumides per un organisme i la massa que n’incorpora com a resultat de l’assimilació.
Per a representar l’eficiència en el flux d’energia total en els nivells heterotròfics, el quocient assimilatori sol ésser calculat en unitats d’energia
progressió aritmètica
Matemàtiques
Progressió en què cada terme,
a k
, és igual a l’anterior,
a k - 1
, més una quantitat constant d
que és anomenada diferència
o raó
de la progressió:
a k
=a k - 1
+ d
.
Un terme qualsevol, a n , pot ésser calculat directament per la fórmula a n = a 1 + n -1 d , i la suma dels primers termes, S n , és donada per la fórmula
aranzel
Economia
Dret fiscal
Impost que paguen els béns importats a un estat i, en alguns casos, certs béns exportats.
Els primers aranzels tenien la finalitat de recaptar fons per al fisc Amb l’adveniment de la industrialització, l’aplicació de l’aranzel respon més pròpiament al desig de protegir la producció nacional de la competència estrangera que a l’obtenció de recursos fiscals L’aranzel pot ésser específic si és calculat prenent com a base una propietat física del producte pes, volum, etc ad valorem, si és calculat sobre el preu, i mixt , si hom fa intervenir elements ad valorem i específics L’aranzel específic té l’avantatge de la simplicitat en la seva aplicació, però té l’…
cicle lunar
Cronologia
Període de temps, transcorregut el qual es tornen a trobar el Sol i la Lluna en les mateixes posicions relatives i, en conseqüència, es repeteixen les fases de la Lluna en les mateixes dates.
El cicle lunar té una durada de 235 llunacions, equivalents a 19 anys tròpics o 6 939,60 dies Fou calculat per primera vegada per l’astrònom grec Metó, juntament amb Euctemó, i és també conegut per cicle de Metó o cicle metònic
fórmula de Maclaurin
Matemàtiques
Fórmula que dóna el desenvolupament en sèrie de Taylor i en el punt x = 0 (teorema de Taylor) d’una funció f(x), real o complexa, derivable fins a l’ordre n + 1.
Representant per f i 0 la derivada d’ordre i de f x en el punt x = 0, la fórmula és on R, anomenat resta o terme complementari, pot ésser calculat a partir de l’expressió on θ és un nombre entre 0 i 1
desgast
Geomorfologia
Hidrografia
Pèrdua de massa d’un còdol a causa del frec originat pel transport.
El desgast és major o menor segons la força de l’element de transport i segons la mida de les partícules transportades És calculat amb l’índex I = 2r/L x 1 000, L essent l’eix més gran del còdol, i r el radi més petit de curvatura
progressió geomètrica
Matemàtiques
Progressió en què cada terme,
a k
, és igual a l’anterior,
a k - 1
, multiplicat per una quantitat constant r
que és anomenada raó
de la progressió:
a k
=
a k - 1 r
.
Un terme qualsevol, a n , pot ésser calculat directament per la fórmula a n = a 1 r n - 1 El producte dels n primers termes, P n és donat per la fórmula Quan r =1, la suma dels n primers termes de la progressió, S n , és donada per la fórmula En el cas que la raó r sigui, en valor absolut, menor que la unitat, hom pot calcular la suma S de tots els termes de la progressió amb la fórmula
volum
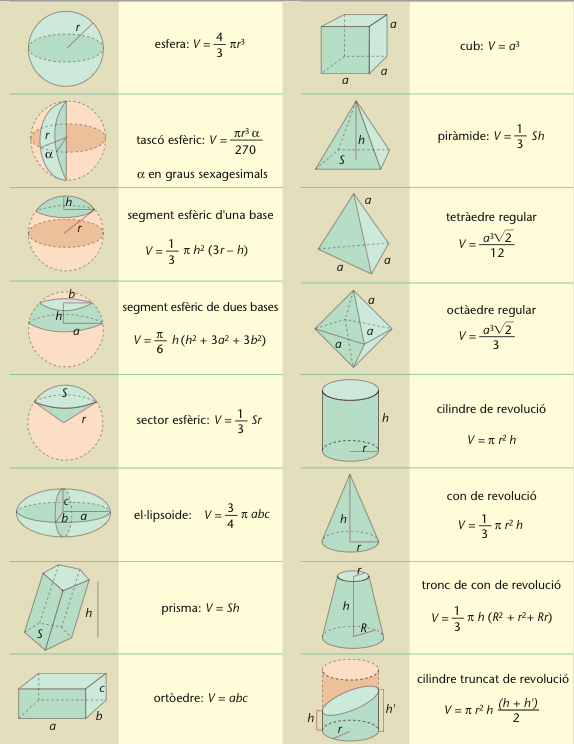
Fórmules per al càlcul de volums
© Fototeca.cat
Matemàtiques
Grandor o mesura de la porció de l’espai ocupada per un cos.
El volum és una mesura que a tota regió de l’espai de tres dimensions assigna un nombre real positiu, de manera que es compleix la propietat additiva, és a dir, que el volum d’un cos és igual a la suma dels volums de qualsevol partició que hom hagi fet en el cos divisió del cos en parts disjuntes Prenent com a base que el volum assignat a un cub de costat a és a 3 , el volum de qualsevol altre cos pot ésser calculat com l’ínfim de la suma dels volums dels cubs disjunts que plegats cobreixen el cos Així, el volum d’una figura plana és zero El volum dels cossos geomètrics simples…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- Pàgina següent
- Última pàgina