Resultats de la cerca
Es mostren 28 resultats
teoria de distribucions
Matemàtiques
Part de l’anàlisi matemàtica (i, en particular, de l’anàlisi funcional) que estudia els funcionals lineals continus sobre l’espai vectorial topològic de les funcions reals infinitament diferenciables de suport compacte de ℝn.
L’origen de la teoria té lloc en el càlcul simbòlic de Heaviside del final del segle XIX, el qual fou emprat sistemàticament pels físics i pels enginyers en la resolució de problemes teòrics d’electricitat Posteriorment, l’any 1926, Dirac introduí la seva funció d delta de Dirac com a instrument de treball que ajuda en el tractament de problemes de mecànica quàntica Paradoxalment, tant en el càlcul simbòlic com en els treballs de Dirac, malgrat que hom cometia una sèrie d’abusos de llenguatge i d’incorreccions matemàtiques, els resultats pràctics eren bons No fou fins després del…
quantitat
Matemàtiques
Qualsevol expressió aritmètica, algèbrica o analítica a la qual hom atribueix un valor.
Una quantitat és tot allò que és susceptible d’augment o disminució i pot ésser mesurat per tal d’ésser expressat amb un nombre Dues quantitats són dites commensurables si hi ha una relació fraccionària entre llurs mesures Una quantitat és infinitament gran si supera una quantitat de referència, que dependrà en cada cas d’una elecció arbitrària, i és infinitament petita si no arriba a aquesta quantitat de referència
anàlisi no estàndard
Matemàtiques
Branca de la lògica matemàtica que fonamenta un càlcul amb infinits i infinitèsims a l’estil de Leibniz.
Hom obté un model no estàndard *R del cos R dels nombres reals com a ultrapotència de R *R és un cos ordenat no arquimedià que conté R i d’altres elements infinitament grans i infinitament petits Per a alguns problemes pot ésser més senzill treballar a *R que no pas a R En tot cas permet una formulació diferent de la pròpia del mètode de Weienstrass amb ε i δ, que pot ésser més intuïtiva Fou desenvolupada per A Robinson a partir del 1960
punt de contacte
Matemàtiques
Punt comú a dues corbes en el qual tenen la mateixa tangent.
Hom diu que aquest contacte M és d’ordre n si es donen dos punts P i P’ infinitament propers a M, un sobre cada corba, tals que la distància PP’ sigui un infinitèsim d’ordre n +1 respecte a l’arc MP i a la corda MP
centre òptic d’una lent
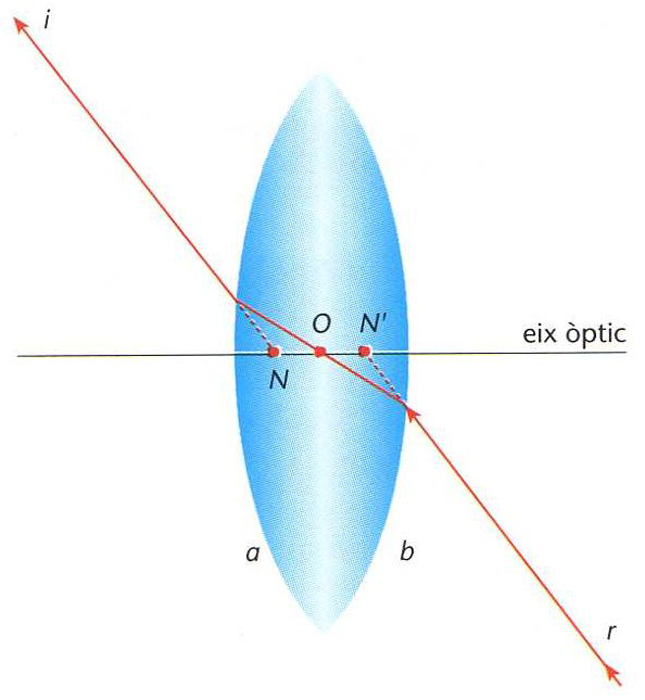
Centre òptic d’una lent
© fototeca.cat
Física
Punt situat a l’interior d’una lent i sobre el seu eix òptic, tal que tot raig que hi passa prové d’un raig incident que és refractat per la lent de tal manera que el raig refractat que en surt és paral·lel a l’incident.
Així doncs, el centre òptic O és la imatge que del punt nodal objecte N de la lent dóna la primera superfície d’aquesta o dioptre d’entrada la imatge d' O donada per la segona superfície de la lent o dioptre de sortida és el punt nodal objecte N ' En l’aproximació d’una lent infinitament prima, els punts O , N , i N ' coincideixen amb el punt d’intersecció de la lent amb l’eix òptic
capacitat
Electrònica i informàtica
Magnitud que expressa l’aptitud que tenen els conductors d’emmagatzemar electricitat en forma de càrrega elèctrica.
La capacitat d’un conductor és definida com el quocient entre la seva càrrega elèctrica i el seu potencial, suposant que tots els altres conductors són infinitament allunyats o bé, si no ho són, que llur potencial és nul La capacitat d’un condensador és el quocient entre la càrrega elèctrica d’una de les armadures i la diferència de potencial existent entre elles El símbol de la capacitat és C , i la seva unitat en el sistema internacional SI, el farad , bé que en la pràctica hom sol emprar els seus submúltiples pel fet d’ésser aquesta unitat massa gran Correntment són emprats el…
polivalent
Lògica
Dit del sistema lògic que, a diferència de la lògica tradicional i de la majoria de les lògiques contemporànies (anomenades bivalents, car només admeten dos valors de veritat: ‘‘és veritable’’ i ‘‘és fals’’), accepta més de dos valors de veritat.
Hom en diu trivalent, tetravalent, etc , segons que siguin tres, quatre, etc , els valors que hi siguin admesos d’altra banda, si aquest nombre de valors és finit, hom parla de lògica finitament polivalent i de lògica infinitament polivalent, si el dit nombre de valors és infinit La lògica polivalent, pròpia del s XX bé que hom en cerca antecedents en Aristòtil i en Guillem d’Occam, amb relació al problema dels futurs i futuribles, s’oposa al principi tradicional del non datur tertium i és típicament exemplificable en l’acceptació que, per exemple, una proporció pot ésser “no…
asímptota
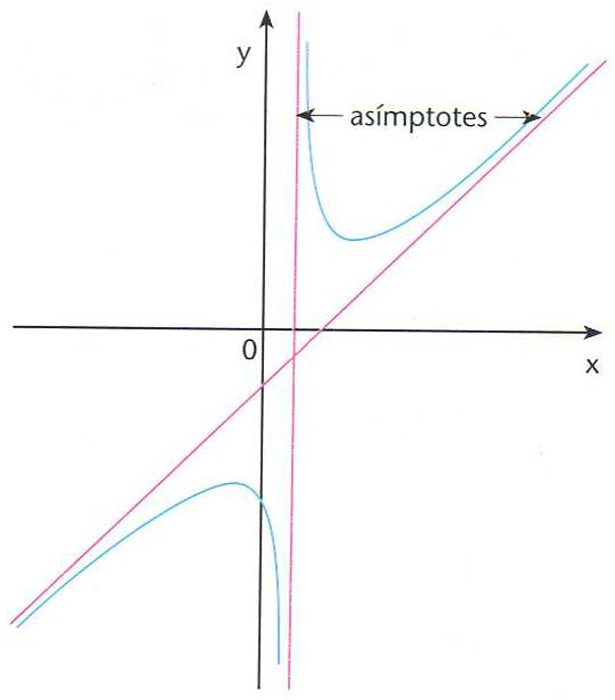
Asímptotes
Matemàtiques
Recta a la qual s’acosta un punt variable sobre una branca de corba quan el punt s’allunya cap a l’infinit.
Per a poder afirmar que una branca de corba té una asímptota cal que, si el punt P es mou sobre aquesta de manera que la distància de P a l’origen de coordenades O creix infinitament, la direcció de la recta OP tingui un límit determinat Hom troba aquest límit per mitjà del quocient y/x = tg a Coneguda la direcció de l’asímptota, hom determina la seva ordenada a l’origen per la condició que la distància entre dos punts que tinguin igual abscissa, un sobre la corba, l’altre sobre l’asímptota, tingui límit zero quan aquella abscissa comuna es fa infinita Així, per exemple, la…