Resultats de la cerca
Es mostren 156 resultats
integral impròpia
Matemàtiques
Integral que, a causa de no ésser definida o fitada, la funció a integrar, en algun punt del seu domini de definició, no és calculable directament.
Així, quan la funció f no és definida o fitada a un punt c del seu domini de definició a,b , hom defineix la integral impròpia de f en a,b per si aquests dos límits existeixen, la integral és anomenada convergent i, en cas contrari, divergent Un altre cas d’integral impròpia s’esdevé quan un dels límits d’integració és infinit la integral és definida aleshores, segons el cas, per Les integrals impròpies són també anomenades integrals generalitzades
integral
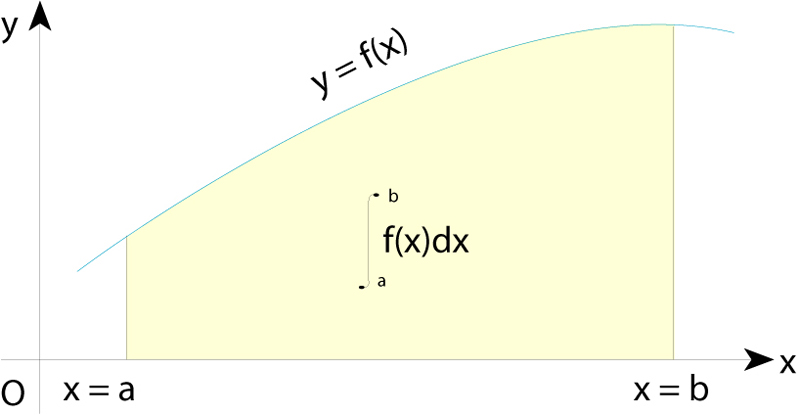
El valor d’una integral definida és igual a l’àrea limitada per la funció, l’eix d’abcisses i les dues ordenades corresponents als extrems de l’interval de definició
© Fototeca.cat
Matemàtiques
En el sentit més general, forma lineal μ sobre certs espais vectorials de funcions, que assigna a cada funció f de l’espai un escalar μ(f) anomenat integral de f.
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann , la integral de Riemann-Stieltjes i la integral de Lebesgue La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques Si a,b és un interval tancat de la recta real, i P={ x 0 ,, x n } és una partició de a,b , és a dir, un conjunt finit de punts tal que a = x 0 ≤ x 1 ≤ ≤ x n = b , sigui Δ x i = x i - 1 per a i =1,, n Si f és una funció fitada definida en a, b ,…
integral múltiple
Matemàtiques
Integral definida sobre un domini D de ℝn.
Donat un domini D de ℝ n , i una partició en dominis elementals D i d’àrees a i i diàmetres d i , i donada una funció real definida sobre D , fD ⊂ ℝ n → ℝ, límit I quan els d i tendeixen a 0, de les sumes de Riemann on A i ∈ D i Hom diu que I és la integral de f en D i és notada per ʃ ʃ n ʃ D ʃ x 1 , x n d x 1 dx n Els casos particulars n =2 i n =3 constitueixen la integral doble i la integral triple, respectivament Les integrals múltiples poden ésser calculades per integració unidimensional reiterada
transformació integral
Matemàtiques
Operació mitjançant la qual una funció f(x) és transformada en una altra funció F(y) gràcies a relacions de tipus integral.
L’exemple més senzill és la simple integració F y = ∫ a y f x dx Una expressió vàlida per a un nombre important de transformacions integrals és F y = ∫ a b K x,y f x dx en la qual K x,y rep el nom de nucli i caracteritza l’esmentada transformació en molts casos, els límits d’integració són 0, ∞ i -∞, ∞ Cal esmentar, com a exemples importants, la integral ponderada, la integral de convolució, la transformada de Fourier anàlisi de Fourier, la de Laplace, la de Kankel, i la de Mellin
integral definida
Matemàtiques
Integral, especialment quan convé distingir-la de la integral indefinida.
integral simple
Matemàtiques
.
Integral, especialment quan convé distingir-la de la integral múltiple
integral primera
Matemàtiques
En una equació diferencial ordinària de segon ordre, equació diferencial ordinària de primer ordre, que resulta de fer una integració en l’equació original.
Així, per exemple, l’equació de la conservació de l’energia mecànica és obtinguda en fer una integració de l’equació del moviment d’un sistema conservatiu hom diu que l’energia és una integral primera del moviment, o, simplement, una integral del moviment