Resultats de la cerca
Es mostren 25 resultats
teoremes de Guldin
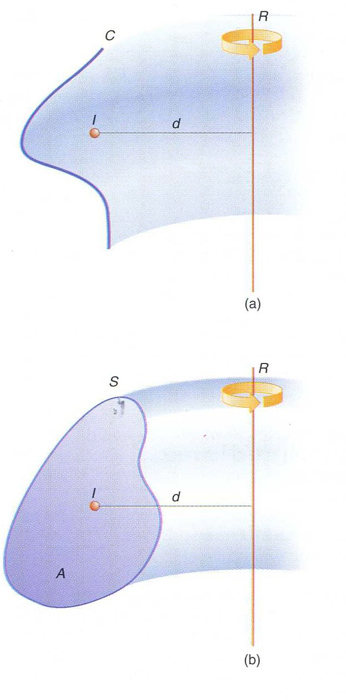
teoremes de Guldin: (a) primer teorema; (b) segon teorema
© fototeca.cat
Matemàtiques
Teoremes que relacionen el centre de massa d’una corba o d’una superfície amb l’àrea o el volum, respectivament, que generen en girar al voltant d’un eix.
Segons el primer teorema de Guldin , donada una corba plana C , de longitud l , que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2π dl , on d és la distància des del centre de massa I de la corba a la recta R en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material El segon teorema de Guldin afirma que, donada una superfície plana S , d’àrea A , que gira al…
teorema
Matemàtiques
Qualsevol proposició matemàtica que pot ésser demostrada a partir d’unes hipòtesis, uns axiomes o altres proposicions demostrades anteriorment.
Les proposicions prèvies de demostració breu que precedeixen un teorema de demostració més complicada són dites lemes , mentre que les conseqüències que es deriven del teorema són anomenades corollaris Hom anomena també teorema qualsevol conclusió general que ja ha estat demostrada Una conjectura , en canvi, és una proposició que hom creu certa però en desconeix la demostració Hi ha nombrosos teoremes coneguts, com ara el de Pitàgores, el de Tales, el del valor mitjà, etc Dos teoremes són anomenats recíprocs quan cadascun té per hipòtesi la conclusió de l’altre
postulat
Lògica
Proposició fonamental d’un sistema deductiu que ni és evident ni pot ésser demostrada.
Tradicionalment el postulat era contraposat a l'axioma, pel fet de no ésser evident ni universalment acceptat, i al teorema, pel fet de no ésser demostrable Actualment, tanmateix, hom assimila el postulat a l’axioma, per tal com pot ésser posada en qüestió la idea d’evidència Més que no el seu caràcter apriorístic, el que hom entén avui com a propi del postulat és la posició primària que aquest ocupa en un sistema formal El sistema de postulats d’una teoria ha d’ésser elegit de tal manera que totes les proposicions de la teoria puguin ésser deduïdes per una cadena de raonaments d’aquells…
lema de Zorn
Matemàtiques
Lema establert pel matemàtic nord-americà d’origen alemany Max Zorn, segons el qual en tot conjunt ordenat inductiu (és a dir, on tot subconjunt totalment ordenat té una fita superior) existeix un element maximal.
Aquest lema o axioma és “equivalent lògicament” a l' axioma de Zermelo i al teorema de Zermelo i d’altres d’enunciats L’ús del lema de Zorn és molt freqüent, en especial per a demostrar teoremes d’existència com ara el referent a la base d’un espai vectorial
formalisme
Matemàtiques
Doctrina segons la qual la matemàtica consisteix simplement en un joc formal amb símbols i regles.
La construcció d’un sistema formal resulta, aleshores, d’obtenir, a partir d’uns axiomes inicials, dels quals pot no existir cap realització concreta i dels quals hom no en qüestiona l’existència “real”, un conjunt consistent de teoremes El formalisme, anomenat a voltes axiomatisme o axiomàtica formal , fou introduït pel matemàtic alemany David Hilbert, i, com a intent de fonamentació de la matemàtica, s’oposa al logicisme de Russell i Whitehead i a l'intuïcionisme de Brouwer
anàlisi funcional
Matemàtiques
Estudi d’espais vectorials topològics els elements dls quals són funcions.
Els espais funcionals més interessants són els de les funcions contínues, el de les funcions integrables i el de les funcions normades Els principals conceptes de l’anàlisi, com la diferenciació i la integració, es poden generalitzar a espais de Banach donant lloc a estudis típics d’anàlisi funcional Té importants aplicacions a l’estudi d’equacions diferencials en derivades parcials, equacions funcionals i integrals, usant teoremes generals com el de Hahn-Banach, el de Riesz o el de l’apliació oberta
convolució
Matemàtiques
Donades dues funcions reals de variable real, f(x) i g(x), funció definida per la integral: .
La convolució, o producte de convolució , té les propietats commutativa, associativa i distributiva Hi ha dos teoremes importants sobre la convolució El primer, o teorema de Parseval , afirma que la transformada de Laplace o de Fourier de la convolució de dues funcions és el producte de les transformades de Laplace o Fourier, respectivament, de les dues funcions F f*g y = Ff y x Fg y Segons el segon, la transformada de Fourier del producte de dues funcions és igual a la convolució de les seves transformades dividit per 2π F f x g y = 1/2π Ff y * Fg y
objecte matemàtic
Matemàtiques
Concepte matemàtic precisat per una definició.
El caràcter matemàtic de l’objecte és donat per la possibilitat d’establir relacions entre aquest i els altres objectes de la teoria, en forma de teoremes, els quals hom dedueix dels axiomes de partença Sovint els objectes matemàtics són classes d’equivalència construïdes a partir d’altres elements anteriors concepte de nombre enter, de direcció, de vector lliure, etc Hom anomena objectes primitius d’una teoria matemàtica aquells que no poden ésser definits a partir d’objectes anteriors i han d’ésser definits establint una sèrie de condicions que els relacionen entre ells, com és…
PROLOG
Electrònica i informàtica
Llenguatge de programació utilitzat en intel·ligència artificial.
És caracteritzat pel fet d’incorporar un motor d'inferències Desenvolupat a principi dels anys setanta per Alain Colmerauer i Philippe Roussel, de Marsella, el seu ús rebé un fort impuls davant la decisió dels japonesos d’adoptar-lo com a llenguatge per al desenvolupament dels anomenats ordinadors de cinquena generació La idea del PROLOG és que la tasca del programador s’ha de reduir a especificar el problema a resoldre, i deixar que el sistema informàtic decideixi com resoldre'l a partir de l’especificació donada Per a l’especificació s’usa una restricció de la forma clausular del llenguatge…
teoria clàssica de camps

Esquema de la teoria clàssica de camps
© Fototeca
Física
Part de la física que estudia els sistemes que són descrits per camps i l’evolució dels quals és predicible (és a dir, que l’estat en un instant t determina totalment l’estat a tot instant posterior t’).
Conceptualment, la teoria pot ésser estructural si les magnituds són les dels components microscòpics, com ara és el cas de l' electrodinàmica clàssica i la relativitat general , o fenomenològica si les magnituds macroscòpiques tenen una interpretació indirecta en termes de la configuració microscòpica, com ara és el cas de la mecànica dels medis continus La dinàmica dels camps clàssics pot ésser derivada d’un principi integral anàleg al principi de Hamilton de la mecànica clàssica, i en resulten les equacions de Lagrange del camp i els teoremes de conservació que són conseqüència de les…