Resultats de la cerca
Es mostren 28 resultats
David James Thouless

David James Thouless
© Trinity Hall / University of Cambridge
Física
Físic britànic.
Graduat a Cambridge 1955, posteriorment estudià les propietats de la matèria a escala nuclear amb Hans Bethe a la Universitat de Cornell, als Estats Units, on el 1958 obtingué el doctorat Després de cursar estudis postdoctorals a les universitats de Berkeley i Birmingham, fou professor de física matemàtica en aquesta universitat 1968-75 Professor de física a la Universitat de Washington, a Seattle, fins a la jubilació 1980-2003, i després professor emèrit, és autor de Quantum Mechanics of Many-Particle Systems 1961 i de Topological Quantum Numbers in Nonrelativistic Physics 1998, entre moltes…
axiomes de separació
Matemàtiques
Axiomes topològics relatius a les possibles separacions entre punts.
En un espai topològic Y , els axiomes són Axioma T 0 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x que no conté y Axioma T 1 Per a qualsevol parell de punts x i y diferents, existeixen un entorn U de x , i un entorn V de y , tals que U no conté y i V no conté el punt x Quan aquest axioma se satisfà, l’espai es diu espai de Fréchet Axioma T 2 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x i un entorn de y sense punts en comú Quan aquest axioma se satisfà, l’espai s’anomena espai de Hausdorff Axioma T 3 Per a cada punt x i tot conjunt…
anàlisi funcional
Matemàtiques
Estudi d’espais vectorials topològics els elements dls quals són funcions.
Els espais funcionals més interessants són els de les funcions contínues, el de les funcions integrables i el de les funcions normades Els principals conceptes de l’anàlisi, com la diferenciació i la integració, es poden generalitzar a espais de Banach donant lloc a estudis típics d’anàlisi funcional Té importants aplicacions a l’estudi d’equacions diferencials en derivades parcials, equacions funcionals i integrals, usant teoremes generals com el de Hahn-Banach, el de Riesz o el de l’apliació oberta
axiomes de numerabilitat
Matemàtiques
Axiomes topològics relatius a la numerabilitat de les bases d’entorns.
El primer axioma de numerabilitat en un espai topològic estipula que cada punt de l’espai té una base d’entorn numerable El segon axioma de numerabilitat postula l’existència d’una base d’oberts numerable en la topologia d’un espai topològic Si un espai topològic satisfà aquest segon axioma s’anomena separable
teoria de distribucions
Matemàtiques
Part de l’anàlisi matemàtica (i, en particular, de l’anàlisi funcional) que estudia els funcionals lineals continus sobre l’espai vectorial topològic de les funcions reals infinitament diferenciables de suport compacte de ℝn.
L’origen de la teoria té lloc en el càlcul simbòlic de Heaviside del final del segle XIX, el qual fou emprat sistemàticament pels físics i pels enginyers en la resolució de problemes teòrics d’electricitat Posteriorment, l’any 1926, Dirac introduí la seva funció d delta de Dirac com a instrument de treball que ajuda en el tractament de problemes de mecànica quàntica Paradoxalment, tant en el càlcul simbòlic com en els treballs de Dirac, malgrat que hom cometia una sèrie d’abusos de llenguatge i d’incorreccions matemàtiques, els resultats pràctics eren bons No fou fins després del 1945 que…
homeomorf | homeomorfa
Matemàtiques
Dit dels espais topològics entre els quals hom pot establir un homeomorfisme.
fluxgrama
Graf orientat equivalent a un diagrama de blocs, però de traçat més senzill.
Els nodes hi representen senyals o variables, i les branques, relacions entre variables La fletxa que porta la branca indica el sentit del flux del senyal, i la lletra associada, el factor de multiplicació transmitància que experimenta el senyal del node d’origen La variable corresponent a un node dependent pren un valor igual a la suma dels senyals incidents En conjunt, el fluxgrama representa un sistema d’equacions algèbriques lineals del tipus y 1 t = a 1 1 y 1 t + a 1 2 y 2 t + + a 1 n y m t y 2 t = a 2 1 y 1 t + a 2 2 y 2 t + + a 2 n y n t y n t = a n 1 y 1 t + a n 2 y 2 t + + a n n y…
grup
Matemàtiques
Estructura algèbrica constituïda per un conjunt G on hi ha definida una operació, designada per *, que per a qualssevol elements a, b, c de G té aquestes tres propietats: propietat associativa, o sia (a*b) *C = a*(b*c); G conté un element neutre e, o sia a*e = a; i per a qualsevol element a n’hi ha un altre de G, representat per a’, que és el seu invers (a*a’ = a’*a = e).
Si a més es compleix la propietat commutativa a*b = b*a , el grup és anomenat commutatiu o abelià i, en aquest cas, si hom representa l’operació amb el signe +, el grup és anomenat també additiu , mentre que si hom utilitza el signe o uns altres, el grup és anomenat també multiplicatiu Hom anomena ordre d’un grup el nombre d’elements que conté més exactament, és el cardinal del conjunt dels seus elements El grup és anomenat cíclic si qualsevol element s’obté per producte repetit d’un de fix, anomenat generador L’estudi en abstracte dels grups permet d’obtenir resultats aplicables a grups…
homologia
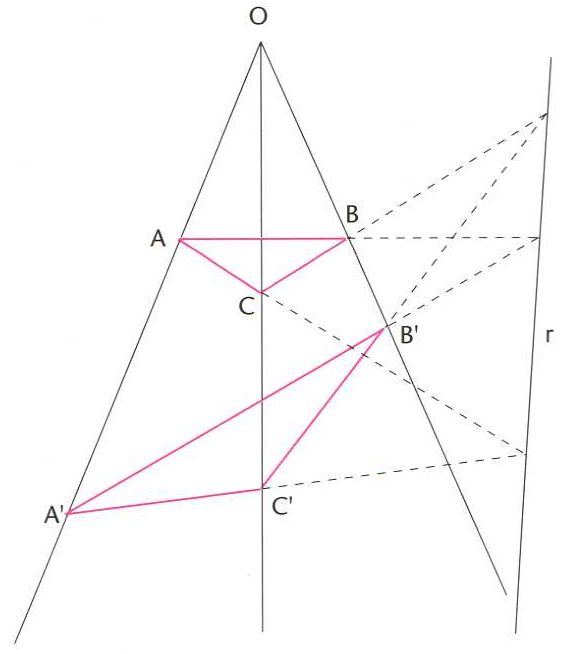
Trasformació per homologia d’un triangle ABC en A'B'C’ (O, centre de l’homologia; r, eix de l’homologia)
© Fototeca.cat
Matemàtiques
Teoria que estudia les transformacions entre espais topològics que conserven certes estructures algèbriques definides en cada espai.
homeomorfisme
Matemàtiques
Aplicació biunívoca f entre dos espais topològics tal que f i la seva inversa f - 1 són contínues.