Resultats de la cerca
Es mostren 3119 resultats
Okrug dels Khantis i dels Mansis
Divisió administrativa
Okrug autònom, a l’oblast’ de T’umen’, a Rússia.
La capital és Khanty-Mansijsk 34 462 h 1989
bescanviador de calor
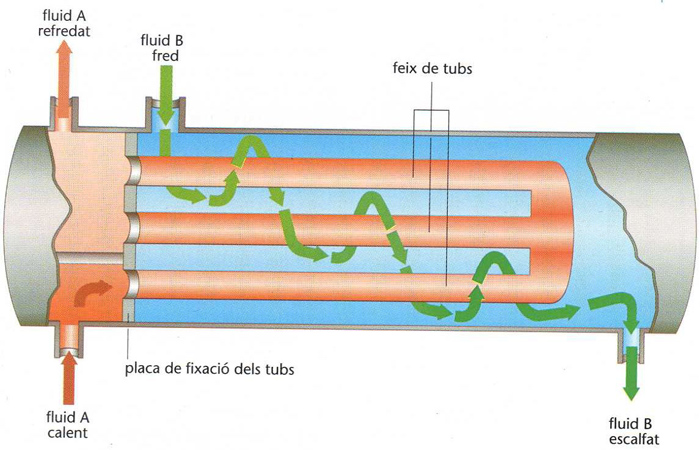
Secció longitudinal esquemàtica d’un bescanviador de calor de feix tubular
© Fototeca.cat
Física
Aparell emprat per a transmetre calor d’un fluid a un altre que és a temperatura inferior.
Aquests circulen, en general, parallelament en el mateix sentit o en sentit contrari, separats per una paret d’un material bon conductor La quantitat de calor cedida per un fluid Q c i l’absorbida per l’altre Q a poden ésser avaluades amb les expressions Q c = MC T o —T 1 i Q a = mc t o —t 1 , on M i m són les masses dels fluids, C i c llurs calors específiques, T o i T 1 les temperatures d’entrada i sortida, respectivament, del fluid primari escalfador, i t o i t 1 les corresponents al fluid secundari escalfat La disposició més corrent consisteix en un cos cilíndric de material…
variable termodinàmica
Física
Cadascuna de les magnituds físiques mútuament compatibles l’especificació del valor de les quals determina un estat en el sistema termodinàmic considerat.
En el cas dels gasos ideals, hom empra la pressió, el volum i la temperatura absoluta, o sia p, V, T Les relacions matemàtiques entre les variables termodinàmiques o d’estat són anomenades equacions d’estat del sistema Per a un gas real, amb pressió crítica p c , temperatura crítica T c i volum molar crític V c , hom defineix les anomenades variables reduïdes mitjançant les relacions p r = p/p c T r = T/T c V r = V/V c , on p, T i V són, respectivament, la pressió, la temperatura i el volum molar en l’estat…
trajectòria
Matemàtiques
En un procés estocàstic, funció real obtinguda en fixar la component aleatòria del procés.
Si X O, T X Ω → R és un procés estocàstic real i per a cada ω ∈ Ω hom considera l’aplicació X ω O,T → R definida per X ω t = X t ,ω, aleshores X ω és una trajectòria corresponent al procés X
equació de Kirchhoff
Física
Equació que relaciona la variació d’entalpia amb la temperatura a pressió constant.
S'expressa per i permet de calcular la variació d’entalpia H d’una reacció a la temperatura T 2 , tot coneixent la variació de l’entalpia de la reacció a una certa temperatura T 1 i les capacitats calorífiques dels productes i dels reactius a T 1 i T 2
factor còsmic d’escala
Astronomia
Variable que explicita la grandària de l’Univers en funció del temps.
Es relaciona amb el paràmetre de desplaçament cap al vermell z , mitjançant l’expressió 1+ z = R t 0 /R t 1 , on t 0 és el temps present i t 1 el temps en què fou emesa la radiació ara desplaçada Es relaciona també amb la constant de Hubble mitjançant l’expressió H 0 = d R/dt/ R La seva variació temporal és relacionada amb el paràmetre de desceleració còsmica
energia d’activació
Química
En cinètica química, la quantitat E que apareix en l’equació empírica d’Arrhenius
.
L’equació dóna la variació de la constant de velocitat k d’una reacció en funció de la temperatura absoluta T L’energia d’activació E suposada independent de T és interpretada com l’energia que han d’assolir conjuntament les molècules dels reactants perquè la reacció tingui lloc, i el fenomen de la catàlisi és interpretat com un abaixament de l’energia d’activació a causa de la presència del catalitzador Independentment de tota hipòtesi, el valor d' E és calculable a partir de dades experimentals amb resultats prou coherents perquè l’equació d’Arrhenius tingui…
subespai
Matemàtiques
Qualsevol subconjunt no buit F d’un espai vectorial E (sobre un cos K) tal, que és estable per a les dues lleis de E i que, proveït d’aquestes lleis induïdes, és també un espai vectorial (sobre K).
En l’espai vectorial de tres dimensions ℝ 3 els subespais són el mateix espai, l’origen de coordenades i totes les rectes i els plans que passen per l’origen F és un subespai de E si, donats qualssevol x , y de F i λ de K , aleshores la combinació lineal x ,-λ y pertany a F Tota família de vectors determina l’anomenada envolupant lineal , o mínim subespai, que els conté La intersecció M ∩ N de dos subespais M i N és un subespai, però la reunió M ∪ N no ho és en general La suma M + N definida per a tots els vectors que són suma d’un element de M i un de N és el mínim subespai que conté la…
allisatge
Matemàtiques
Conjunt de mètodes per al tractament de dades estadístiques de tipus cronològic o sèries temporals, que tenen per objecte fer previsions a curt termini basades en les dades anteriors.
Hom tracta de separar la fluctuació aleatòria de la llei subjacent del fenomen, allisant els valors històrics anteriors La més emprada és la tècnica anomenada de les mitjanes mòbils , que pren com a previsió la mitjana aritmètica de les N darreres dades Hom pot veure fàcilment que S t +1 = S t + X t — X t-N /N Si es tracta, p ex, de preveure les vendes d’un producte per al més següent t+ 1, hom pren la mitjana dels darrers dotze mesos, amb la qual cosa hom suposa que s’eliminaran les variacions aleatòries El mètode de l'…
axiomes de separació
Matemàtiques
Axiomes topològics relatius a les possibles separacions entre punts.
En un espai topològic Y , els axiomes són Axioma T 0 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x que no conté y Axioma T 1 Per a qualsevol parell de punts x i y diferents, existeixen un entorn U de x , i un entorn V de y , tals que U no conté y i V no conté el punt x Quan aquest axioma se satisfà, l’espai es diu espai de Fréchet Axioma T 2 Per a qualsevol parell de punts x i y diferents, existeix un entorn de x i un entorn de y sense punts en comú Quan aquest axioma se satisfà, l’espai s’anomena espai de Hausdorff Axioma T 3 Per a…
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- …
- Pàgina següent
- Última pàgina