Resultats de la cerca
Es mostren 5896 resultats
derivada direccional d’una funció en un punt
Matemàtiques
Donada una funció D ⊂ℝ n →ℝ, un punt a∈D, i un vector no nul v∈ℝ n , límit, si existeix, del quocient [f( a+h v) - f( a)]/h, quan h tendeix a zero.
Si aquest límit existeix hom el nota per f ´ a , v , i hom diu que f és derivable en la direcció v en el punt a i que f ´ a , v és la derivada de f en la direcció en el punt a Les derivades parcials són derivades en la direcció dels vectors unitaris canònics de ℝ n
equació de Laplace
Física
Matemàtiques
Equació diferencial en derivades parcials expressada per la fórmula Δf = 0, Δ essent el laplacià.
Les funcions que són solució de l’equació de Laplace són anomenades funcions harmòniques , i tenen una especial aplicació en la teoria del potencial En el cas que f sigui una funció de la variable complexa z = x + iy , l’equació de Laplace, que en aquest cas pren la forma ∂ 2 f /∂ x 2 + ∂ 2 f /∂ y 2 = 0, expressa la condició necessària i suficient perquè f sigui derivable
lliscament
Electrònica i informàtica
En una màquina elèctrica asíncrona, relació entre la diferència de la velocitat de sincronisme nf i la del rotor n, i la de sincronisme nf del camp magnètic de l’estator.
El lliscament és, doncs, s = n f -n / n f
sèrie de potències
Matemàtiques
Donada una funció real de variable real f (x) derivable indefinidament en el punt x0, sèrie Σ an (x-x0)n amb an = (1/ n !) fn (x0).
Es compleix que f x = Σ a n x- x 0 n per a tots els punts x tals que | x- x 0 | < R, on R és el radi de convergència de la sèrie Aquesta sèrie és anomenada sèrie que desenvolupa la funció f en un entorn del punt x 0 , o sèrie de Taylor de f en el punt x 0 La sèrie de potències és utilitzada per a expressar el desenvolupament en sèrie d’una funció Així, per exemple, hom té la sèrie exponencial , que és convergent per a tot x
paràmetre de Coriolis
Geografia
Component de l’acceleració de Coriolis de més pes en les equacions de la dinàmica marina que és designada generalment per la lletra f = 2 W sin f, on W és la velocitat angular de la Terra i f és la latitud.
A les latituds mitjanes, f és de l’ordre de 7×10 - 5 s - 1
corba bipolar
Matemàtiques
Corba plana que pot ésser definida com el conjunt de punts les coordenades bipolars dels quals, respecte a dos focus F i F´, satisfan una determinada relació, anomenada equació bipolar de la corba.
P ex, l’ellipse és determinada pel fet que els seus punts satisfan r + r' = 2 a , essent a el semieix major i r i r' les distàncies dels punts als focus F i F'
focus imatge
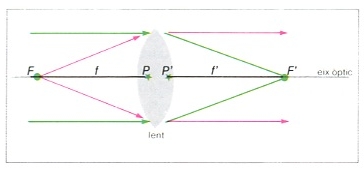
focus objecte
F i focus imatge F’ d’una lent; la distància focal objecte f és la distància entre el punt principal objecte P i el focus objecte F , la distància focal imatge f’ és la distància entre el punt principal imatge P’ i el focus imatge F’Física
Punt on convergeixen els raigs de llum que han incidit sobre el sistema paral·lelament a l’eix òptic.
independència funcional
Matemàtiques
Propietat de què gaudeix una família de funcions f1, f2, ..., fn quan no existeix cap funció F tal, que F(f1, f2, ..., fn) = 0, on (F (f1, f2, ..., fn) (x) = F(f1 (x), f2 (x), ..., fn(x).
Vegeu també jacobià
autovalor
Matemàtiques
En un endomorfisme f d’un espai vectorial, valor numèric λ per al qual existeix un vector no nul v (autovector) tal que f(v) = λv.
En espais de dimensió finita, els autovalors coincideixen amb els zeros del polinomi característic, és a dir, amb els valors numèrics λ tals que det A - λI = 0, on A és la matriu de l’endomorfisme f i la I la matriu identitat
teorema de Taylor
Matemàtiques
Teorema que dóna el desenvolupament en sèrie d’una funció f(x), fixat un punt a.
Si f x és una funció d’una variable real i derivable n vegades, la fórmula que expressa el teorema de Taylor és Els n +1 primers sumands d’aquesta expressió són coneguts com a polinomi de Taylor de grau n , per a f en el punt a , mentre que el terme R n+1 a x és anomenat resta Aquest terme compleix la següent condició d’aproximació És, per tant, un infinitèsim d’ordre superior a x-a n , i pot ésser expresat per qualsevol de les dues maneres següents per a algun t ∈ a,x , per a algun t ∈ a,x En el cas que f n⁺ 1 es pugui integrar en a,x , hom té l’expressió integral de…