Resultats de la cerca
Es mostren 578 resultats
Emil Artin
Matemàtiques
Matemàtic alemany.
A partir del 1925 fou professor a la Universitat d’Hamburg, però el 1937 se n'anà als EUA El 1958 retornà a la Universitat d’Hamburg És un dels principals exponents de la moderna escola alemanya i els seus treballs han obert noves vies de recerca en tots els camps de l’àlgebra moderna, principalment en teoria dels nombres i en geometria algèbrica Les seves publicacions més importants són Theorie der Gammafunktion 1931, Galois theory 1942, Geometric algebra 1957 i Field Theory 1961
Teó d’Esmirna
Música
Filòsof i matemàtic grec.
Vida S’inscriví plenament en el gran corrent d’idees platonicopitagòriques que veia en la música un dels llocs paradigmàtics on es pot copsar la proporció existent entre totes les coses Teó emprà la paraula mousiké per a indicar tant la pràctica musical com aquesta proporció omnipresent És per això que en les Qüestions necessàries per a la comprensió de Plató , únic text complet que s’ha conservat dels molts que escriví, pot plantejar-se de copsar la música en el cosmos, en els nombres i en els instruments musicals
Émile Joseph Maurice Chevé
Música
Teòric de la música i pedagog francès.
Arran del seu matrimoni amb la cantant Nanine Paris, abandonà la carrera de metge per a dedicar-se a la teoria musical, i més específicament del cant Juntament amb el seu cunyat Aimé Paris, desenvolupà un nou mètode de notació musical, basat en el meloplasto de Pierre Galin, en el qual cadascun dels nombres de l’1 al 7 equivalia a un grau de l’escala mètode Galin-Paris-Chevé Acèrrim defensor del nou mètode, intentà provocar debats públics sobre el tema i enfrontaments entre els seus seguidors i els partidaris del sistema tradicional
model atòmic de Sommerfeld
Física
Ampliació del model atòmic de Bohr, realitzada per A.Sommerfeld l’any 1915.
Consisteix essencialment a suposar que les òrbites electròniques són ellíptiques —el nucli atòmic essent un dels focus de la corba— i a aplicar a les integrals d’acció principi de la mínima acció pròpies del moviment electrònic una quantificació Aquest model introduí el total de nombres quàntics azimutals, però hi ha certes diferències entre llurs valors i els observats experimentalment, raó per la qual, malgrat que permeté en alguns casos d’explicar la multiplicitat observada en l’espectre de ratlles, fou aviat superat pel model basat en la mecànica quàntica model atòmic de Schrödinger
índex
Matemàtiques
Equació matemàtica utilitzada per a obtenir els valors de la variació d’un fenomen determinat.
L’índex estadístic sol ésser anomenat també taxa, coeficient o ràtio Emprada sobretot en econometria i demografia, la presentació de dades en forma de nombres-índex permet, en economia, d’analitzar d’una manera sintètica, l’evolució corresponent Hom parla, així, d’índex simple índex de preus, de producció d’una mercaderia, etc quan hi són expressades variacions d’una sola magnitud i d’índex compost índex del cost de la vida, de preus a l’engròs, etc quan hi és recollida la variació conjunta de magnituds diverses
projecció fitada
Matemàtiques
Sistema de projecció que utilitza només com a pla de projecció el pla horitzontal i substitueix el vertical per un nombre.
Aquest nombre, que indica la distància del punt al pla, és escrit al costat de la projecció horitzontal en una unitat determinada El pla de projecció rep el nom de pla de comparació i els nombres escrits amb cada projecció són anomenats fites Així, un punt és determinat per la seva situació a l’espai respecte al pla de comparació i la seva fita Per distingir els punts que hi ha a sobre del pla de comparació dels que hi ha a sota, els primers porten la fita positiva i els segons negativa
funció sinus
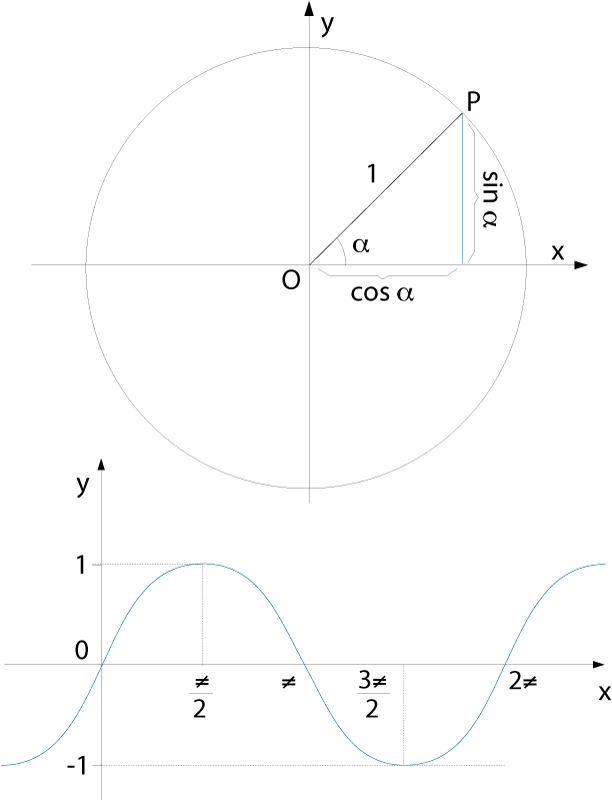
Representació gràfica del sinus d’un angle (a dalt) i de la funció sinus (a baix)
© Fototeca.cat
Matemàtiques
Funció sin: ℝ→ℝdefinida per l’assignació x →sin (x) on sin(x) és el sinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1,1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció cosinus per la derivada d sin x / dx =cos x , d cos x / dx = -sin x És indefinidament derivable i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió sin x= e i x - e i x /2 i , relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció sinus complex
funció cosinus
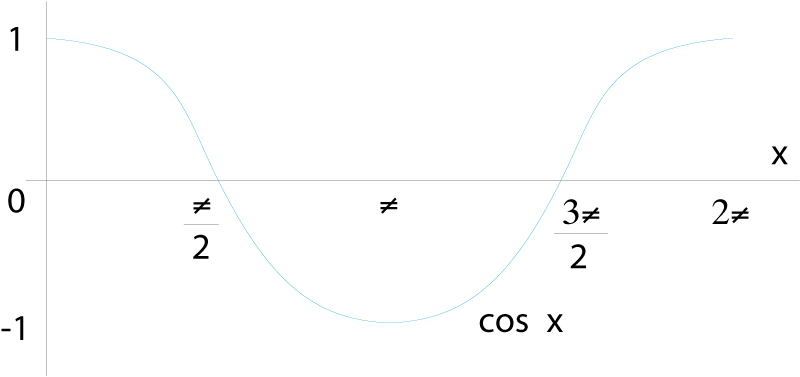
Representació gràfica de la funció y=cos x
© Fototeca.cat
Matemàtiques
Funció cos: ℝ→ℝdefinida per l’assignació x →cos (x), on cos(x) és el cosinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1, 1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció sinus per la derivada dcos x/ dx = -sin x, dsin x/ dx = cos x És indefinidament derivable, i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió cos x=e i x + e - i x /2, relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció cosinus complex
algorisme
Lògica
Matemàtiques
Procediment de càlcul que amb un conjunt ordenat i finit d’instruccions, de símbols i regles o d’operacions, permet trobar la solució d’un problema pas a pas o de forma recursiva.
S’aplica en tots els casos en què l’ús d’una estratègia ordenada i iterativa facilita l’obtenció de solucions Destaquen els algorismes típicament numèrics com el de calcular arrels quadrades o cúbiques, o l’algorisme d’Euclides, per a calcular el màxim comú divisor de dos nombres enters, però també són molt importants avui els algorismes subjacents a molts programes informàtics vàlids per a càlculs matemàtics, així com per a moltes altres aplicacions optimització, jocs, organització, etc Rep el nom del matemàtic persa Muḥammad ibn Mūsà al-Ḫwārizmī
Roman Opałka
Pintura
Pintor polonès establert a França.
Fill d’emigrants polonesos a França, l’any 1935 retornà a Polònia, d’on fou deportat amb la seva família a Alemanya l’any 1940 Novament a França després de l’alliberament, el 1946 retornà a Polònia De la segona meitat dels anys quaranta fins a mitjan anys cinquanta aprengué la tècnica de la litografia i estudià art i disseny a Łódź i belles arts a Varsòvia L’any 1957 viatjà a París, i entre el 1959 i el 1963 féu una sèrie de pintures monocromes en blanc El 1965 començà OPAŁKA 1965/1-∞, l’obra a la qual es dedicà pocs anys més tard exclusivament, consistent en una sèrie de teles de dimensions…
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- …
- Pàgina següent
- Última pàgina