Resultats de la cerca
Es mostren 6227 resultats
funció cosinus
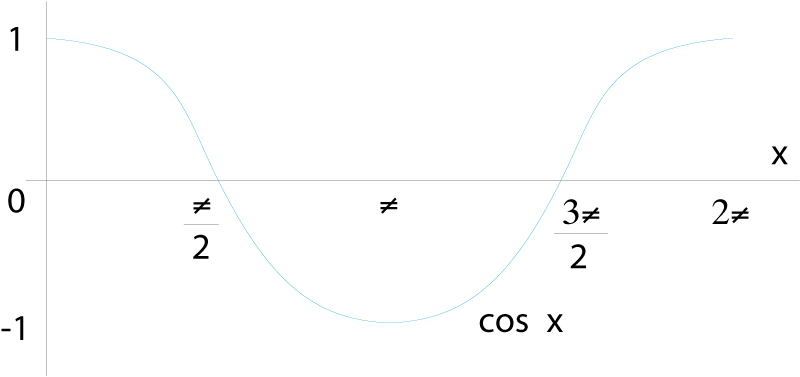
Representació gràfica de la funció y=cos x
© Fototeca.cat
Matemàtiques
Funció cos: ℝ→ℝdefinida per l’assignació x →cos (x), on cos(x) és el cosinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1, 1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció sinus per la derivada dcos x/ dx = -sin x, dsin x/ dx = cos x És indefinidament derivable, i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió cos x=e i x + e - i x /2, relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció cosinus complex
funció còncava
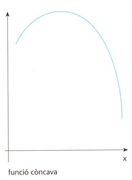
Funció concàva
© Fototeca.cat
Matemàtiques
Funció f:(a,b)⊂ℝ→ℝtal que per a tot α∈(0,1) se satisfà f(αx+(1—α)y)≥αf(x)+(1—α)f(y), on a<x<b i a<y<b.
El significat geomètric és que per a tot interval x,y ⊂ a,b la corda que uneix f x amb f y és situada per sota de l’arc que uneix f x amb f y
funció convexa
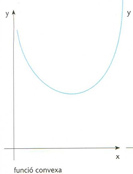
Funció convexa
© Fototeca.cat
Matemàtiques
Funció f:(a,b)⊂ℝ→ℝtal que per a tot α∈(0,1) se satisfà f(αx+(1-α)y)≤αf(x)+1-α)f(y), on a<x<b i a<y<b.
El significat geomètric és que per a tot interval x,y ⊂ a,b la corda que uneix f x amb f y és situada per sobre de l’arc que uneix f x amb f y
funció cotangent
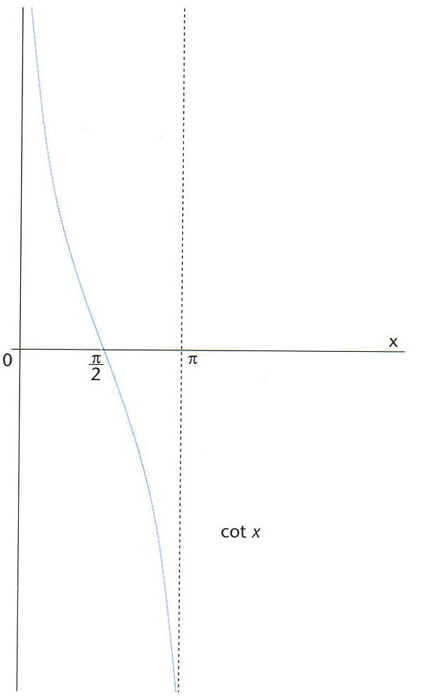
Representació gràfica de la funció cotangent
© Fototeca.cat
Matemàtiques
Funció cotg: ℝ-{kπ,k∈ℤ}→ℝ, definida per l’assignació x→1/tg, on tg és la funció tangent.
funció sinus
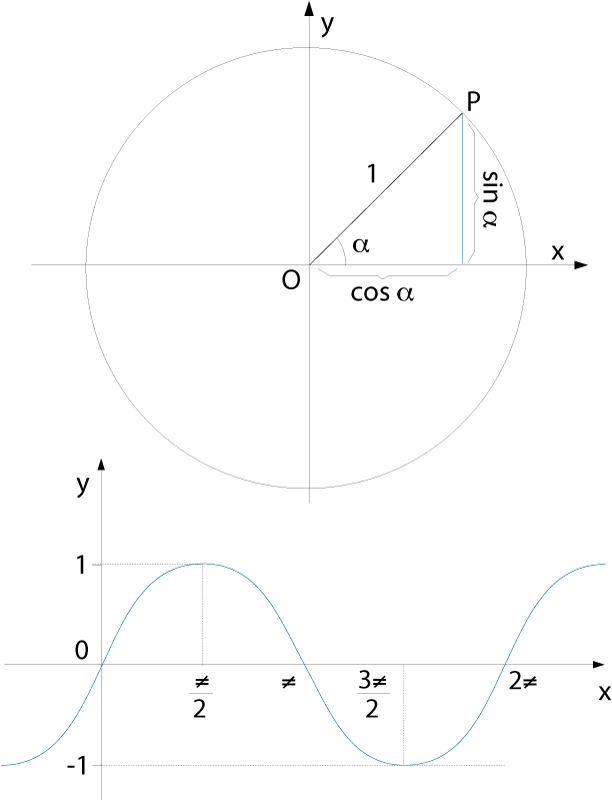
Representació gràfica del sinus d’un angle (a dalt) i de la funció sinus (a baix)
© Fototeca.cat
Matemàtiques
Funció sin: ℝ→ℝdefinida per l’assignació x →sin (x) on sin(x) és el sinus de l’angle que fa x radiants.
És una funció periòdica de període 2π i el seu recorregut és l’interval -1,1 És una de les sis funcions trigonomètriques o circulars i està relacionada amb la funció cosinus per la derivada d sin x / dx =cos x , d cos x / dx = -sin x És indefinidament derivable i el seu desenvolupament en sèrie entera és En termes de la funció exponencial complexa té l’expressió sin x= e i x - e i x /2 i , relació que permet d’estendre-la al cos dels nombres complexos, resultant-ne la funció sinus complex
funció característica
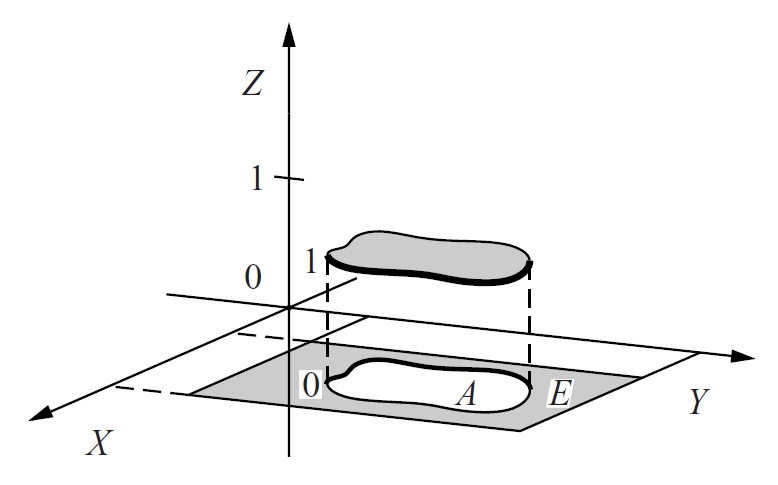
Gràfica de la funció característica del subconjunt A del domini E del pla
Matemàtiques
Funció construïda a partir de la funció de distribució d’una variable aleatòria que, per derivació, permet calcular els seus moments n-èsims i l’estudi de les distribucions de probabilitat de variables aleatòries compostes.
funció diferenciable
Matemàtiques
En el cas d’una funció f:D⊂ℝ→ℝ,funció derivable
.
En el cas d’una funció qualsevol, funció que admet diferencial
funció zeta
Matemàtiques
Funció complexa, introduïda per Riemann.
Definida per la fórmula on z = x + iy ∈ℂés tal, que x > 1 i ln n és real És una funció meromorfa amb un pol simple en z = 1
funció holomorfa
Matemàtiques
Funció f
: U
⊂ℂ→ℂque té la propietat d’holomorfia.
La funció f definida sobre l’obert U és holomorfa en el punt z 0 ∈ U si és derivable en z 0 , és a dir, si existeix el límit La funció f és holomorfa en un obert U si és holomorfa en tot punt de U La funció f és holomorfa a l’infinit si existeix un nombre real positiu a tal que, per a tot z ∈ℂque verifiqui | z |> a, f és holomorfa en z
funció multiforme
Matemàtiques
Funció que assigna diverses imatges a cada element del domini de definició.
En són exemple les funcions trigonomètriques inverses arc sin1 = {π/2, π/2+2π, π/2+4π,,π/2+2 n π,} Les funcions multiformes no són, en el sentit estricte del terme funcions , sinó correspondències Una funció multiforme esdevé una funció quan hom n'escull una branca o determinació per exemple, la funció Arc sin x és la branca de la funció multiforme arc sin x definida en restringir a 0,2π el recorregut d’aquesta