Resultats de la cerca
Es mostren 243 resultats
Teoria de la calor, sèries de Fourier (Fourier); geometria projectiva, construccions; teorema de Feuerbach (Poncelet)
Teoria de la calor, sèries de Fourier Fourier geometria projectiva, construccions teorema de Feuerbach Poncelet
Construcció de polígons, teoria de nombres, geometria diferencial, geometria no euclidiana, teorema fonamental d’àlgebra, astronomia, geodèsia, grans problemes (Gauss)
Construcció de polígons, teoria de nombres, geometria diferencial, geometria no euclidiana, teorema fonamental d’àlgebra, astronomia, geodèsia, grans problemes Gauss
neguentropia
Física
Electrònica i informàtica
Entropia negativa.
El concepte, introduït per LBrillouin, té un significat invers del de l’entropia si aquesta mesura el grau de desordre d’un sistema, la neguentropia mesura el grau d’ordre d’un sistema Com més gran és la informació que hom posseeix sobre l’estat d’un sistema, tant més gran és la neguentropia El teorema de Szilard-Brillouin , que generalitza el segon principi de la termodinàmica, afirma que, en un sistema aïllat, la suma de la informació i de la neguentropia no pot més que disminuir, tot restant constant a les transformacions reversibles
K-teoria, teorema d’índex d’operadors el·líptics (Atiyal-Singer); topologia diferencial (S. Snade); àlgebra homològica i algebraica. K-teoria (A. Grothendieck)
K-teoria, teorema d’índex d’operadors ellíptics Atiyal-Singer topologia diferencial S Snade àlgebra homològica i algebraica K-teoria A Grothendieck
punt fix
Matemàtiques
En una aplicació f, punt x que verifica la condició f(x) = x.
També és anomenat punt doble Per exemple, el centre de simetria és un punt doble en la simetria central Brouwer ha demostrat l’anomenat teorema del punt fix , segons el qual tota aplicació contínua en una esfera n -dimensional amb ng 2 té un punt fix El teorema té com a conseqüència que la major part de les deformacions físiques tinguin punts fixos
teoremes de Guldin
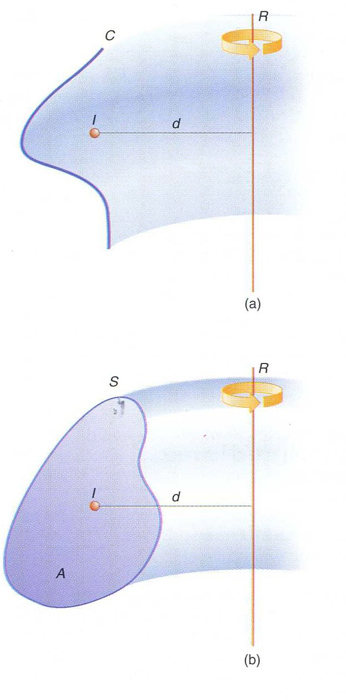
teoremes de Guldin: (a) primer teorema; (b) segon teorema
© fototeca.cat
Matemàtiques
Teoremes que relacionen el centre de massa d’una corba o d’una superfície amb l’àrea o el volum, respectivament, que generen en girar al voltant d’un eix.
Segons el primer teorema de Guldin , donada una corba plana C , de longitud l , que gira al voltant d’una recta R del seu pla, la qual no talla, l’àrea A de la superfície de revolució que genera és A = 2π dl , on d és la distància des del centre de massa I de la corba a la recta R en el cas purament geomètric, el centre de massa és calculat assignant la mateixa “massa” a tots els punts de la corba matemàtica en el cas físic, el centre de massa és el del sistema de masses puntuals de la corba material El segon teorema de Guldin afirma que, donada una superfície plana…
llei de les àrees
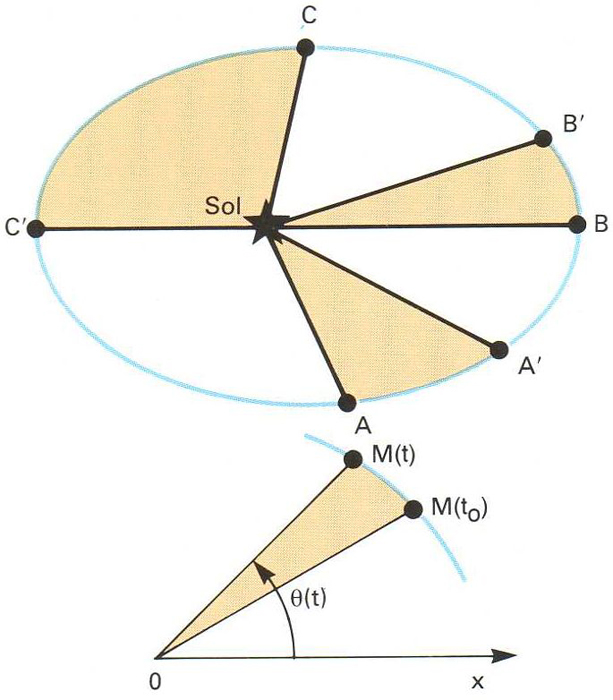
Llei de les àrees aplicada a l’òrbita d’un planeta: les àrees contingudes entre els punts AA’, BB’ i CC’ són iguals perquè es recorren en temps iguals. El radi vector escombra àrees iguals en temps iguals
© fototeca.cat
Física
Teorema referit al moviment d’un punt sotmès a un sistema de forces centrals, que demostra que les àrees descrites pels radis vectors r
©són proporcionals al temps emprat per a descriure-les.
En astronomia, aquest teorema és aplicat a l’estudi del moviment d’un planeta respecte al Sol i és conegut com la segona de les tres lleis de Kepler La demostració és obtinguda d’aplicar el teorema del moment angular al cas particular del moviment d’un punt material M sotmès a un sistema de forces centrals que passen pel punt O , respecte al qual hom obté els moments Aquests moments tenen una resultant nulla i, per tant, el moment angular L és un vector constant perpendicular sempre als radis vectors, que descriuran com a conseqüència una trajectòria plana Si hom…
llei dels grans nombres
Matemàtiques
Teorema intuït per Jakob Bernoulli i P.S.Laplace i batejat així per S.D.Poisson, la demostració del qual, progressivament més i més rigorosa, començà amb P.L.Čebyšev i ha acabat amb E.F.E.Borel, Khinčin, A.N.Kolmogorov, Glivenko i Cantelli.
Una primera formulació de la llei dels grans nombres és la llei feble dels grans nombres , anomenada també teorema de Bernoulli, que estableix que la freqüència relativa d’un esdeveniment al llarg de n temptatives elementals independents convergeix en probabilitat vers la probabilitat de l’esdeveniment Hom diu que una variable aleatòria X n convergeix en probabilitat vers una variable certa A quan la diferència | X n —A | tendeix a 0 en augmentar n , és a dir, quan ε essent tan petit com hom vulgui Una altra formulació de la llei dels grans nombres és l’anomenada llei forta dels…
Nikolaj Jegorovič Žukovskij
Física
Matemàtiques
Físic i matemàtic rus.
Professor a Moscou, féu estudis sobre mecànica teòrica, i a partir del 1900 s’especialitzà en aeronàutica i aerodinàmica, camps en els quals treballà extensament Entre els seus resultats cal destacar el teorema que establí l’any 1905 sobre moviment dels fluids, teorema que el 1902 havia donat a conèixer independentment el físic alemany Martin Wilhelm Kutta Pittschen, 1867 - Stuttgart, 1944, anomenat teorema de Kutta-Žukovskij
Léon Thévenin
Física
Físic francès.
Féu recerques en electricitat, on donà a conèixer el 1883 un conegut teorema, que duu el seu nom, sobre els circuits elèctrics teorema de Thévenin
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- …
- Pàgina següent
- Última pàgina