Resultats de la cerca
Es mostren 27 resultats
Garrett Birkhoff

Garrett Birkhoff
Matemàtiques
Matemàtic i físic nord-americà.
A partir dels anys trenta inicià l’estudi de diverses branques de l’àlgebra moderna que conduïren a la creació de l’àlgebra universal Estudià algebres lliures, teoremes d’isomorfisme i d’homomorfisme, reticles de congruències, reticles en general, sistemes equacionals, etc També cal remarcar les seves contribucions en mecànica de fluids, anàlisi numèrica i teoria nuclear
reticle
Física
Conjunt de dos fils o més creuats que hom posa als focus de certs instruments òptics i que serveix per a efectuar mesures de precisió.
Algunes vegades els reticles són constituïts per fils metàllics, però hom ha fet servir sovint fils d’aranya Aquests darrers tenen una gran extensibilitat, i, per tant, és fàcil de tenir-los sempre tensos, és a dir, rectilinis Actualment hom fa servir en molts aparells un reticle constituït per una placa molt prima de vidre sobre la qual ha estat gravada amb un diamant una sèrie de traços molt fins, que fan el paper dels fils d’aranya clàssics Hi ha també reticles que són emprats especialment en astronomia i formen part dels anomenats oculars micromètrics En general…
alidada
Geografia
Aparell que serveix per a definir visuals i per a traçar-les simultàniament sobre la planxeta topogràfica.
Després de la plomada és, potser, l’instrument topogràfic més antic Consisteix en un regle amb una pínnula perpendicular a cada un dels seus extrems Una és la pínnula ocular, i l’altra, l’objectiva En forma més elaborada consta d’una ullera i reticles, i serveix també per a mesurar angles verticals Molts aparells topogràfics tenen una alidada incorporada
exfoliació
Mineralogia i petrografia
Propietat que tenen certs cristalls de trencar-se en superfícies paral·leles a una cara cristal·lina possible.
Segons el grau d’exfoliació hom l’anomena perfecta, bona, clara i no clara L’exfoliació reflecteix l’estructura interna, puix que els enllaços estructurals no tenen la mateixa força en els diferents plans En els reticles de caràcter fullat, la unió a cada làmina és molt més forta que la que hi ha entre una làmina i les seves veïnes, i en aquest tipus d’estructures l’exfoliació és perfecta i sempre parallela a les fulles, com en la mica i en el grafit
Marshall Harvey Stone
Matemàtiques
Matemàtic nord-americà.
Estudià a la Universitat de Harvard 1919-22, on fou deixeble de George Birkhoff, es doctorà 1926 i fou professor del 1933 al 1946 Des d’aquest any fins a la jubilació 1968, exercí la docència a la Universitat de Chicago, on aconseguí de reunir un dels millors equips de matemàtics Mac Lane, Whitney, AWeil, Zygmund, etc del seu temps Publicà més de 350 treballs i han estat fonamentals les seves aportacions a la teoria de reticles, anàlisi funcional, topologia, teoria de categories, filosofia de la ciència, etc
fosforescència
Física
Emissió de radiació deguda a transicions electròniques en les quals l’estat excitat i l’estat normal tenen diferent spin.
Aquesta emissió, a diferència de la fluorescència, persisteix durant un quant temos després de suprimida l’excitació Primerament la seva intensitat disminueix segons una funció exponencial del temps com la fluorescència, i després més lentament, segons una cinètica més complicada Els espectres de l’emissió fluorescent i de la fosforescent solen ésser idèntics, i la superior persistència de la segona sorgeix del fet que determinats estats electrònics metaestables són “congelats”, i n'esdevé necessària l’excitació tèrmica per a produir l’emissió Moltes vegades aquests estats corresponen als…
reticle
Matemàtiques
Conjunt ordenat en el qual dos elements qualssevol tenen un suprem (la més petita de les fites superiors o elements majorants) i un ínfim (la més gran de les fites inferiors o elements minorants).
És anomenat també conjunt reticular Si C, ≤ és un “ordenat” que és reticle, donats a i b de C, existeix un element, anomenat suprem c = a ∪ b tal, que a ≤ c , b ≤ c , i si a < d i b < d és c < d i un element, dit ínfim , c = a ∩ b tal, que c < a, c < b i si d ≤a, d ≤ b , és d ≤ c El conjunt de parts d’un conjunt respecte a l’ordre definit per la inclusió és un reticle Exemple si A i B són dos conjunts qualssevol, el conjunt més petit que els conté és la seva reunió o suprem i el més gran contingut és la seva intersecció o ínfim La teoria de reticles nasqué amb l…
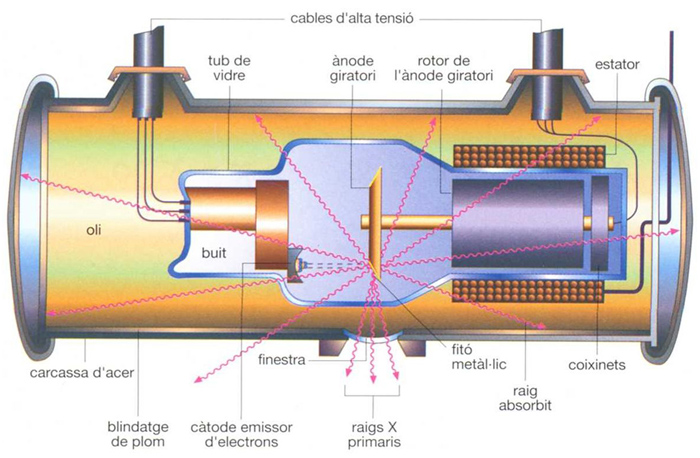
raigs X
fototeca.cat
©
Física
Radiació electromagnètica de freqüència superior a la visible emesa per un àtom en produir-se el salt d’un electró d’una òrbita externa a una d’interna, pel fet d’haver perdut aquesta un electró per efecte d’una excitació exterior o d’una absorció per part del nucli (captura K).
En l’espectre de les ones electromagnètiques els raigs X es troben en la franja de longituds d’ona compresa entre 100 Å i 10 -6 Å El nom de raigs X els fou donat per WC Röntgen el 1895, en descobrir-los i desconèixer-ne la natura Correntment hom els obté per impacte sobre un fitó metàllic de platí o tungstè d’electrons accelerats mitjançant una diferència de potencial d’uns quants milers de volts això té lloc a l’interior d’un tub de vidre tancat on ha estat fet un buit elevat Hi ha dos tipus de tubs productors de raigs X els de càtode fred i els de càtode calent Els primers són tubs de raigs…
carbur
Química
Compost binari de carboni en el qual aquest element és unit a un altre d’electronegativitat semblant o menor.
No són, però, considerats carburs, per convenció, els hidrurs de carboni o hidrocarburs Hom classifica els carburs en tres tipus carburs salins , formats amb metalls dels grups I, II i III de la taula periòdica, substàncies iòniques descomponibles per l’aigua i pels àcids diluïts amb despreniment d’hidrocarburs gasosos uns contenen l’anió C 4 - el d’alumini Al 4 C 3 , el de berilli Be 2 C i alliberen metà per hidròlisi d’altres contenen l’anió C 2 - i alliberen acetilè, i llur estructura i llur comportament són els d’un acetilur d’altres, encara, contenen l’anió C 4 - 3 i desprenen propí per…
àlgebra universal
Matemàtiques
Té com a objecte l’estudi de les operacions finitàries definides en un conjunt, amb l’objectiu de trobar i desenvolupar les propietats que tenen en comú estructures algèbriques diverses, com ara anells, cossos, àlgebres de Boole, reticles, grups, etc.
Aquesta teoria, la inicià Garret Birkhoff a l’entorn del 1930 i fou consolidada després de la Segona Guerra Mundial per Alfred Traski, Leon Henkin i Abraham Robinson, entre d’altres