Resultats de la cerca
Es mostren 3270 resultats
Joan Ventallol
Matemàtiques
Matemàtic.
Publicà un tractat de monedes, pesos i mesures de Mallorca i altres regnes, amb les correspondències Pràctica mercantívol Lió 1521 Traduït al castellà per Joan Baptista Tolrà, fou publicat també a Lió el 1524 i a Tarragona el 1619 Fou tingut en compte per Antic Roca en la seva Arithmetica 1565
integral
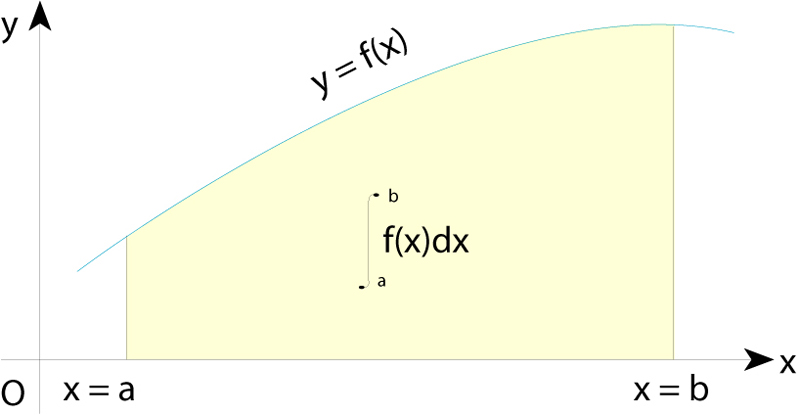
El valor d’una integral definida és igual a l’àrea limitada per la funció, l’eix d’abcisses i les dues ordenades corresponents als extrems de l’interval de definició
© Fototeca.cat
Matemàtiques
En el sentit més general, forma lineal μ sobre certs espais vectorials de funcions, que assigna a cada funció f de l’espai un escalar μ(f) anomenat integral de f.
Hom distingeix entre tres tipus fonamentals d’integral, la integral de Riemann , la integral de Riemann-Stieltjes i la integral de Lebesgue La integral de Riemann té una interpretació geomètrica simple per tal com fou definida a fi de calcular àrees i volums de figures geomètriques Si a,b és un interval tancat de la recta real, i P={ x 0 ,, x n } és una partició de a,b , és a dir, un conjunt finit de punts tal que a = x 0 ≤ x 1 ≤ ≤ x n = b , sigui Δ x i = x i - 1 per a i =1,, n Si f és una funció fitada definida en a, b , hom determina en cada subinterval x i - 1 , x i els termes M i…
permutació
Matemàtiques
Aplicació d’un conjunt de n elements a n llocs diferents, és a dir, cadascun dels diferents arranjaments lineals que es poden fer amb diferents elements, entrant tots ells en cadascun dels arranjaments.
El nombre de permutacions diferents que hom pot fer amb un conjunt de n elements és n n factorial i és donat per la fórmula n = n n- 1 n -2 2 × 1 Si hom identifica alguns dels elements del conjunt, obté les permutacions amb repetició Si el conjunt és identificat en classes de n 1 , n 2 n r elements, el nombre de permutacions amb repetició és n / n 1 n 2 n r Si hom suposa que els llocs són disposats en un cercle i que no es distingeix entre dues permutacions si només difereixen en una rotació, hom obté les permutacions circulars , tant amb repetició com sense Llur nombre, en tots…
base dual
Matemàtiques
Base definida en un espai vectorial E de dimensió finita.
Si e 1 , e n és una base de E , aleshores el conjunt de formes lineals f i E→K, amb imatges sobre el cos K de l’espai vectorial, definits per f i e j =δ i j , essent δ i j =0 si i ≠ j , δ ij =1, forma una base de l’espai dual E *, i s’anomena la base dual de la inicial
teoria de distribucions
Matemàtiques
Part de l’anàlisi matemàtica (i, en particular, de l’anàlisi funcional) que estudia els funcionals lineals continus sobre l’espai vectorial topològic de les funcions reals infinitament diferenciables de suport compacte de ℝn.
L’origen de la teoria té lloc en el càlcul simbòlic de Heaviside del final del segle XIX, el qual fou emprat sistemàticament pels físics i pels enginyers en la resolució de problemes teòrics d’electricitat Posteriorment, l’any 1926, Dirac introduí la seva funció d delta de Dirac com a instrument de treball que ajuda en el tractament de problemes de mecànica quàntica Paradoxalment, tant en el càlcul simbòlic com en els treballs de Dirac, malgrat que hom cometia una sèrie d’abusos de llenguatge i d’incorreccions matemàtiques, els resultats pràctics eren bons No fou fins després del 1945 que…
projectivitat
Matemàtiques
Transformació projectiva, és a dir, aplicació injectiva entre dos plans projectius no necessàriament diferents (f: p* →p*’, que transforma conjunts de punts col·lineals en conjunts de punts col·lineals.
L’estudi de les propietats del pla projectiu invariants sota una projectivitat són l’objecte d’estudi de la geometria projectiva Si f és una projectivitat, es demostra que el transformat x' , y' d’un punt x , y es troba per les equacions i que tota transformació donada per les anteriors equacions és una projectivitat plana, és a dir, que els punts x, y tals que a 3 x + b 3 y + c 3 = 0 es transformen en els punts impropis del pla projectiu
convergència
Matemàtiques
Qualitat de convergent.
En el cas d’una successió de funcions hom pot parlar de convergència en diferents sentits, segons la topologia donada en el conjunt de funcions a considerar així, hi ha la convergència puntual una successió f n tendeix a f si, per a tot x on les f n estan definides, f n x té límit f x la convergència uniforme f n convergeix uniformement a f si, per a tot ε> 0, es dona un N tal, que n> N implica | f n x - f x |
divergència
Matemàtiques
Operador diferencial.
Aquest assigna a una funció vectorial V x la quantitat escalar on V x , V y i V z són les components de V x Hom representa també div V per ∇ V
cònica
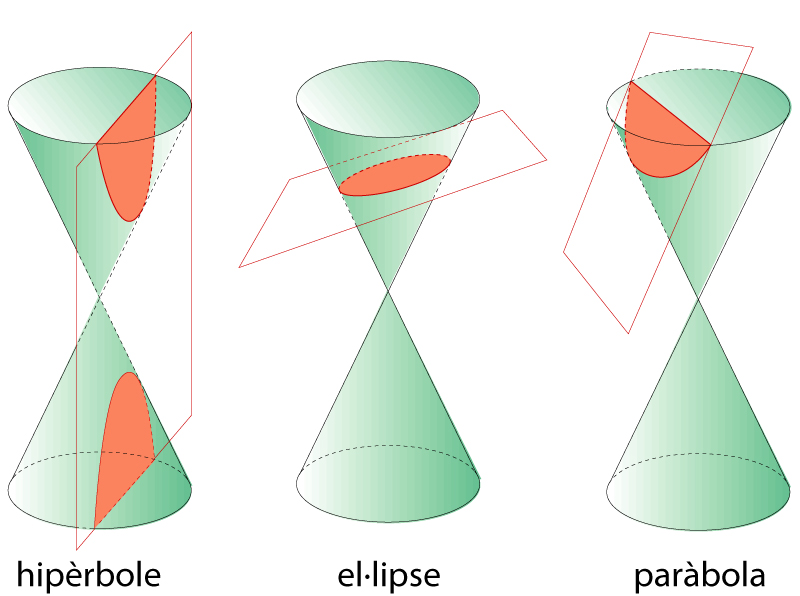
Còniques com a secció de cons
© Fototeca.cat
Matemàtiques
Corba de segon grau en un pla.
El primer estudi conegut sobre còniques és el tractat d’Apolloni de Perge, que les definia com a possibles seccions d’un con Projectivament, hom defineix la cònica com a lloc geomètric dels punts dobles d’una polaritat L’estudi afí de les còniques destaca els següents elements centre , que és el pol de la recta de l’infinit, diàmetre , qualsevol recta que passa pel centre, asímptotes , els diàmetres tangents a la cònica En l’estudi euclidià hom distingeix, a més, els eixos principals, que són una parella de diàmetres perpendiculars i també conjugats respecte a la polaritat induïda per la…
correlació
Matemàtiques
Grau d’interdependència entre diverses variables o, dit d’una altra manera, entre diferents conjunts de nombres.
Si els valors de les diferents variables satisfan exactament una equació, hom diu que hi ha una correlació perfecta entre elles Quan hi ha dues variables, és anomenada correlació simple , i si el nombre de variables és superior a dues, correlació múltiple Donades dues variables aleatòries X , Y , la localització dels parells de punts X, Y damunt un sistema de coordenades rectangular rep el nom de diagrama de dispersió Si tots els punts del diagrama semblen trobar-se aproximadament damunt una recta, hom diu que la correlació és lineal quan els punts descriuen amb una certa aproximació una…