Resultats de la cerca
Es mostren 3270 resultats
funció hipergeomètrica
Matemàtiques
Funció F α β γ:I ⊂ℂ→ℂ, definida per F α β γ(z)=F(α,β,γ; z).
I és el disc | z | i F α,β,γ z és la suma de la sèrie hipergeomètrica per al valor z de la variable És solució de l’equació diferencial z 2 - z y' + 1+α+β z -γ y´ +αβ y = 0
funció hiperbòlica inversa
Matemàtiques
Nom genèric de les funcions inverses de les funcions hiperbòliques, és a dir nom genèric de les funcions argument sinus hiperbòlic (arg sh), argument cosinus hiperbòlic (arg ch), argument tangent hiperbòlica (arg th) i argument cotangent hiperbòlica (arg coth).
funció hiperbòlica complexa
Matemàtiques
Nom genèric de les funcions que resulten d’estendre al cos ℂ les funcions hiperbòliques (sinus hiperbòlic, cosinus hiperbòlic, tangent hiperbòlica, i cotangent hiperbòlica).
funció hiperbòlica
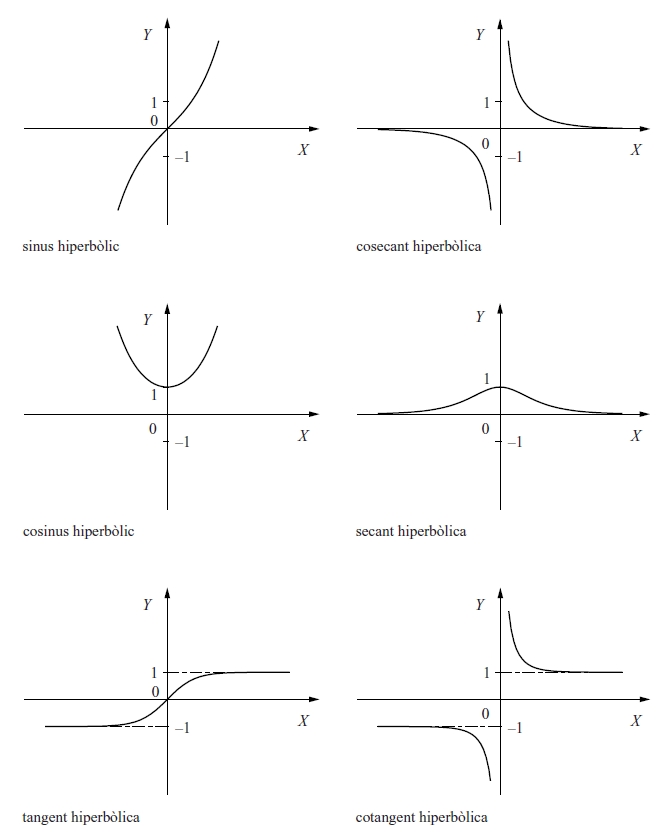
funcions hiperbòliques
Matemàtiques
Nom genèric de les funcions (sinus hiperbòlic (sh), cosinus hiperbòlic (ch), tangent hiperbòlica (th), cotangent hiperbòlica (coth), etc.), definibles en referència a la funció exponencial i lligades a la hipèrbola, de la mateixa manera que les funcions trigonomètriques estan lligades al cercle.
funció harmònica
Matemàtiques
Funció f:ℝ n →ℝque és solució de l’equació de Laplace, és a dir que satisfà Δf≡∇2 f=∂2 f/∂x1 2 +...+∂2 f/∂xn 2 =0.
A més a més hom exigeix, generalment, que f sigui definida en un obert U ⊂ℝ n que hi sigui contínuament diferenciable dues vegades
funció generatriu d’un conjunt de funcions
Matemàtiques
Funció de dues variables f
( z,u
) tal que el seu desenvolupament en sèrie de potències respecte a una de les variables, p ex u
, té com a coeficients d’aquestes potències les funcions del conjunt en qüestió.
Així, la funció és la funció generatriu de les funcions de Bessel d’índex enter, J n z
funció fitada
Matemàtiques
Funció tal que el recorregut és un conjunt fitat.
En el cas f D ⊂ℝ→ℝ, és fitada si existeix una fita M ∈ℝtal que | f x |≤ M per a tot x ∈ D
funció exponencial complexa
Matemàtiques
Funció f:ℂ→ℂque resulat d’estendre a ℂla funció exponencial.
És anomenada també, simplement, exponencial complexa És definida per l’assignació on z ∈ℂ És periòdica de període 2π i És relacionada amb les funcions trigonomètriques sinus i cosinus per la relació e x + i y = e x cos y + sin y , que permet excriure la forma exponencial d’un nombre complex, z = x + iy = ρ e i ϑ on és el mòdul de z i ϑ = arc tg y/x n'és l’argument
funció exponencial
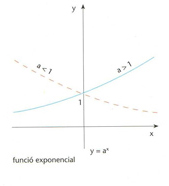
Funció exponencial
© Fototeca.cat
Matemàtiques
Funció contínua f
:ℝ→ℝ +
-{0} que satisfà f
( x
+ x
’) = f
( x
) f
( x
’), per a tot parell x,x
’∈ℝ, i f
(1)= a
, essent a
un nombre real concret que la caracteritza, anomenat base
.
És denotada per l’assignació x → a x És la funció inversa de la funció logarítmica de base Hom empra, especialment, la funció exponencial que té per base el nombre e aquesta és la inversa de la funció logarítmica neperiana ln e x = e l n x = x Quan hom no especifica la base, hom parla de funció exponencial o simplement d’exponencial, tot sobreentenent que es tracta de la funció exponencial de base e , i la nota e x o exp x Té la propietat d e x / dx = e x , i admet el desenvolupament en sèrie Aquesta sèrie convergeix també en el cos ℂ, la qual cosa permet de definir-hi la funció…