Resultats de la cerca
Es mostren 1349 resultats
el·líptic | el·líptica
angle en el centre
Matemàtiques
Angle que té el vèrtex al centre d’una circumferència i els costats del qual són dos radis.
Val igual que l’arc que subtendeix
el·lipsoide
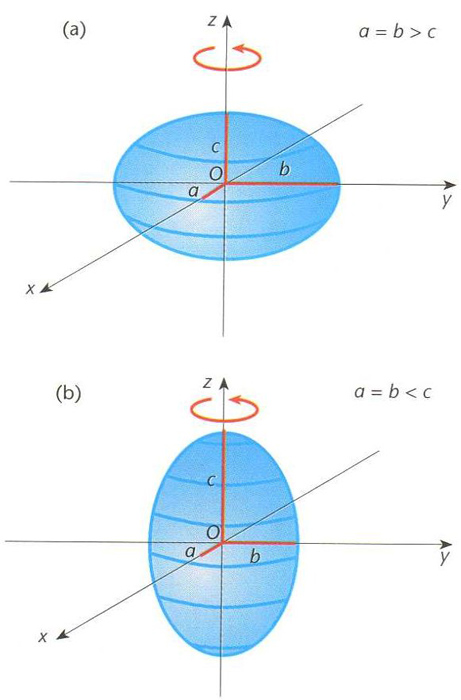
El·lipsoide aplatat (a) i allargat (b) obtinguts per rotació d’una el·lipse, prenent com a eix de la rotació el que conté, en el primer cas, el semieix menor d’aquesta el·lipse i, en el segon, el semieix major
© Fototeca.cat
Matemàtiques
Superfície de segon grau o quàdrica amb centre l’equació de la qual és (
x 2
/a 2
)+(
y 2
/b 2
)+(
z 2
/c 2
)=1 si els eixos de coordenades són els propis de la quàdrica.
Una ellipse que giri al voltant del seu eix menor determina un ellipsoide aplatat , anomenat també esferoide oblat i una ellipse que giri al voltant del seu eix major determina un ellipsoide allargat , anomenat també esferoide prolat Quan a=b=c=r l’ellipsoide esdevé una esfera de radi r
el·lipse
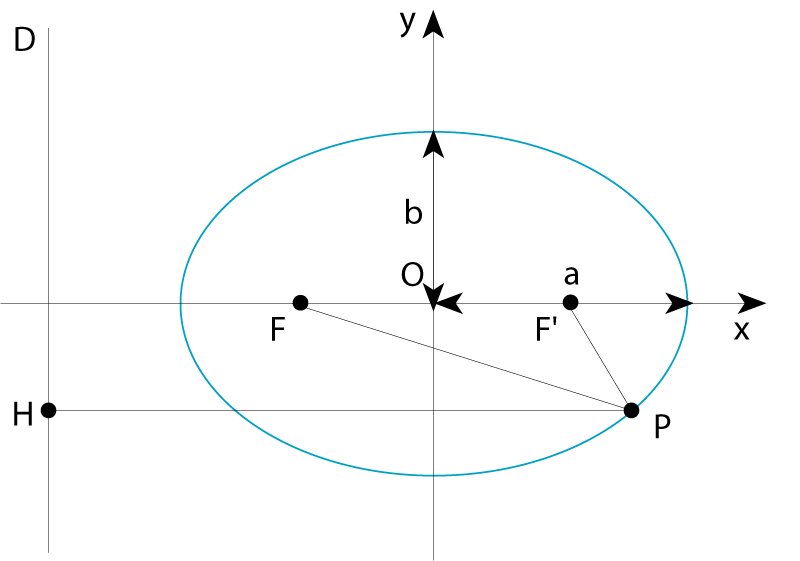
El·lipse de semieixos a i b; D és la directriu associada al focus F
© Fototeca.cat
Matemàtiques
Corba tancada que resulta de la intersecció d’una superfície cònica amb un pla que no és paral·lel a cap generatriu ni a l’eix d’aquella; és doncs, una cònica
.
La seva equació en coordenades cartesianes referides als seus dos eixos perpendiculars de simetria és x 2 / a 2 + y 2 / b 2 =1, a essent el semieix major i b el semieix menor L’ellipse és el lloc geomètric dels punts P del pla tals que la suma de llurs distàncies a dos punts fixos F i F ´, anomenats focus , és una quantitat constant, independent del punt P concret, igual al doble del semieix major, PF + PF ´=2 a és també el lloc geomètric dels punts P tals que el quocient de llurs distàncies a un punt fix, un dels focus, i a…
el·lipsògraf
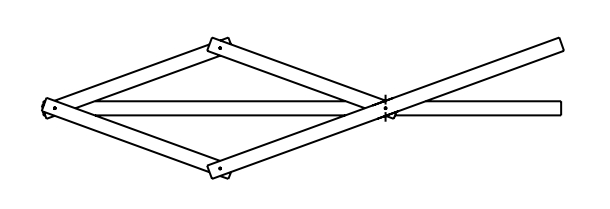
El·lipsògraf de quadrants
derivació sota el signe integral
Matemàtiques
Derivació d’una funció expressada mitjançant una expressió integral.
Així, si fx = ∫ b a F x,y dy, aleshores la seva derivada és donada per l’expressió integral f'x = ∫ b a ∂F x,y /∂ x dy Aquesta forma d’obtenir la derivada és anomenada regla de Leibniz
integral el·líptica
Matemàtiques
Integral de tipus ∫ Rdz
on φ(z) és un polinomi en z de grau 3 o 4 i amb coeficients complexos, i on R
(i, w) és una funció racional de variables independents z,w.
Aquest nom prové del fet que, en intentar rectificar un arc d’ellipse és a dir, en intentar calcular la longitud d’un arc d’ellipse, sorgeix una integral d’aquesta mena Tota integral ellíptica pot ésser transformada per canvis adequats de variables com una suma d’integrals elíptiques elementals Les integrals ellíptiques elementals són de tres tipus integral ellíptica de primer tipus integral ellíptica de segon tipus integral ellíptica de tercer tipus Quan una integral ellíptica s’ha descompost en suma d’integrals ellíptiques elementas es troba en forma estàndard de Legendre-Jacobi
funció el·líptica
Matemàtiques
Funció f:ℂ→ℂdoblement periòdica i meromorfa en ℂ.
En són exemples les funcions ellíptiques de Jacobi i la funció ellíptica de Weierstrass
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina