Resultats de la cerca
Es mostren 1241 resultats
demostració per recurrència
Matemàtiques
Mètode de demostració que consisteix a demostrar que una proposició és veritable per a 1 i que si és veritat per a n tamb é ho és per a n + 1.
D’això hom dedueix que la proposició és veritable per a tot n
definició per recurrència
Matemàtiques
Definició d’una funció sobre els nombres naturals definint-la per a 1 i, per a cada n més gran que 1, en funció dels valors que pren per a nombres més petits que n
.
Per exemple, la funció factorial pot ésser definida fent 1 = 1 i, per a un n > 1, fent n = n -1 n Aquests procediments de demostració i de definició, ja coneguts i emprats pels grecs, han estat generalitzats i ara hom utilitza les recurrències a qualsevol conjunt ben ordenat on tot subconjunt té mínim Aleshores, per a demostrar que una proposició és veritable per a tot element del conjunt ben ordenat, basta demostrar que és veritable per a tot element si ja ho és per a tots els anteriors
tant per cent
Matemàtiques
Proporció d’una quantitat respecte a una altra referida al valor 100 com a unitat.
L' a per cent indicat a % d’una quantitat b és la quantitat a×b /100 És anomenat també percentatge
grup engendrat per una de les seves parts
Matemàtiques
Grup que coincideix amb el subgrup engendrat per una de les seves parts.
subgrup engendrat per una part d’un grup
Matemàtiques
Si A és una part no buida d’un grup G, subgrup que resulta de la intersecció de la família de subgrups de G que contenen A.
Hom diu, aleshores, que aquest és el subgrup de G engendrat per A És, per tant, el menor subgrup de G que conté A
volum
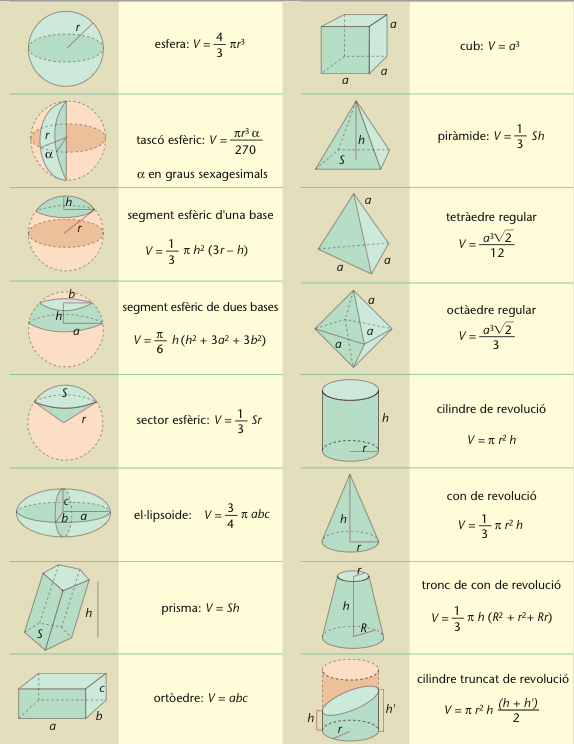
Fórmules per al càlcul de volums
© Fototeca.cat
Matemàtiques
Grandor o mesura de la porció de l’espai ocupada per un cos.
El volum és una mesura que a tota regió de l’espai de tres dimensions assigna un nombre real positiu, de manera que es compleix la propietat additiva, és a dir, que el volum d’un cos és igual a la suma dels volums de qualsevol partició que hom hagi fet en el cos divisió del cos en parts disjuntes Prenent com a base que el volum assignat a un cub de costat a és a 3 , el volum de qualsevol altre cos pot ésser calculat com l’ínfim de la suma dels volums dels cubs disjunts que plegats cobreixen el cos Així, el volum d’una figura plana és zero El volum dels cossos geomètrics simples pot ésser…
simetria
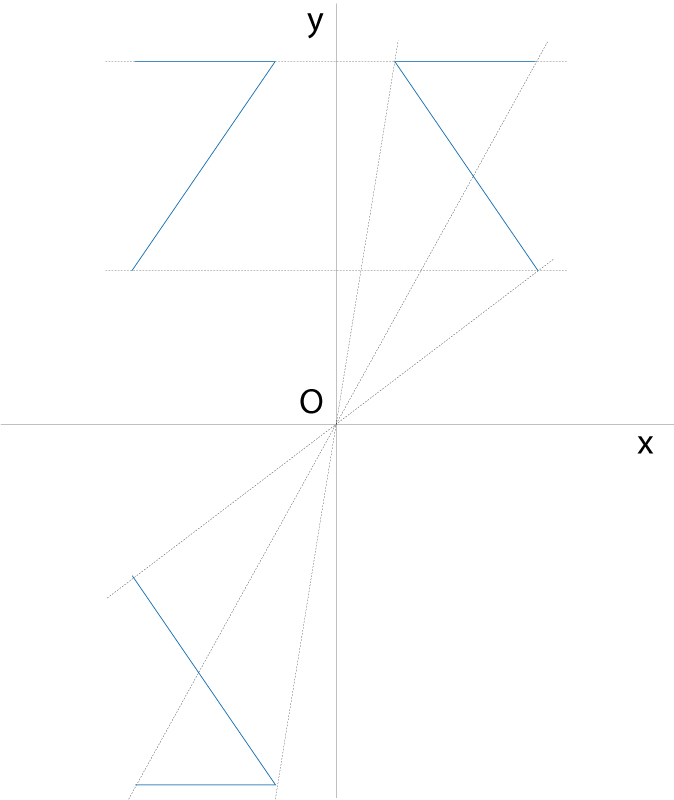
Dues figures obtingudes per simetria axial i central
© Fototeca.cat
Matemàtiques
Configuració d’un objecte que és invariant per a determinats moviments geomètrics.
Dins el concepte de simetria hom estudia modernament tots el moviments geomètrics del pla i de l’espai Una simetria axial és la transformació que per a tot punt P n'assigna un altre P' , de manera que la recta PP' és perpendicular a una recta donada dita eix de simetria i les distàncies de P a l’eix i de P' a l’eix són iguals Una simetria especular és la transformació que per a tot punt P n'assigna un altre P' , de manera que la recta PP' és perpendicular a un pla donat dit pla de simetria i les distàncies de P al pla i de P' al pla són iguals Una simetria central…
tor
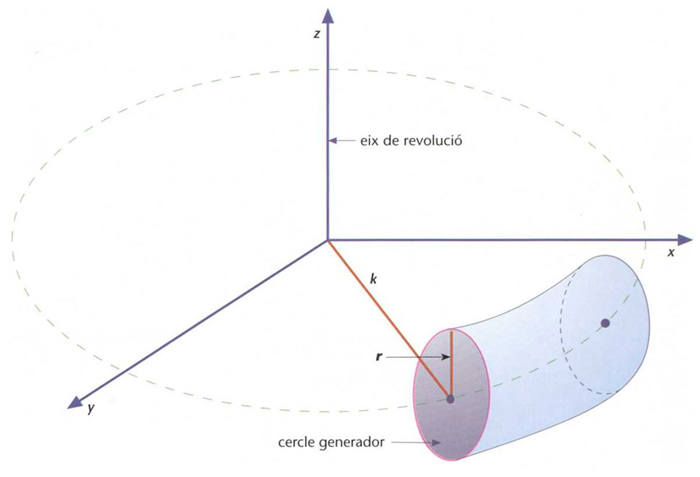
Generació d’un tor per un cercle
© Fototeca.cat
Matemàtiques
Superfície generada per la rotació, en l’espai, d’un cercle al voltant d’un eix del seu pla que no talla el cercle.
És la forma d’un anell de contorn circular i rodó Si r és el valor del radi del cercle generador, k la distància del centre a l’eix de revolució eix z , l’equació del tor és el seu volum val 2π kr, i l’àrea de la seva superfície, 4 π 2 kr
bisector
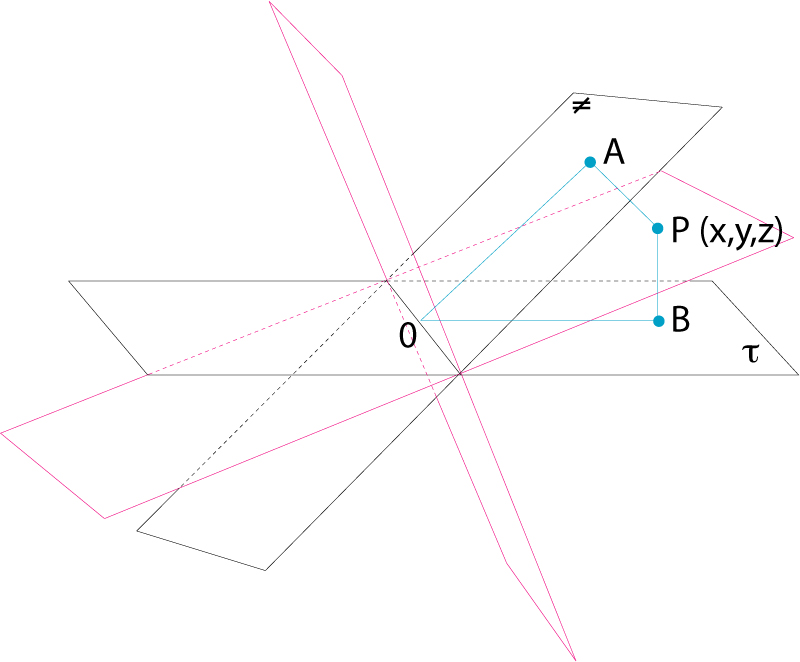
Plans bisectors dels quatre díedres formats per dos plans donats que es tallen
© Fototeca.cat
Matemàtiques
Lloc geomètric dels punts que equidisten dels dos plans costats d’un angle díedre, el qual, per tant, és dividit en dos díedres iguals.
Dos plans no parallels determinen quatre angles díedres, per als quals hom distingeix dos plans bisectors Per a cada díedre, un dels plans bisectors serà interior, i l’altre, exterior Si les equacions cartesianes de dos plans són A 1 x + B 1 y + C 1 z + D 1 = 0 i A 2 x + B 2 y + C 2 z + D 2 = 0, en una referència cartesiana normal, l’equació dels dos plans bisectors dels díedres que aquells determinen és
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina