Resultats de la cerca
Es mostren 23 resultats
arrel de la unitat
Matemàtiques
Qualsevol nombre complex z
tal que
z n
= 1, per a algun n
.
Les arrels de la unitat són cos k 360°/ n + i sin k 360°/ n en variar k= 0,1,2,, n -1 Aquestes arrels formen un grup respecte a la multiplicació i són igualment distribuïdes sobre el cercle de radi 1 en el pla complex
teorema de Taylor
Matemàtiques
Teorema que dóna el desenvolupament en sèrie d’una funció f(x), fixat un punt a.
Si f x és una funció d’una variable real i derivable n vegades, la fórmula que expressa el teorema de Taylor és Els n +1 primers sumands d’aquesta expressió són coneguts com a polinomi de Taylor de grau n , per a f en el punt a , mentre que el terme R n+1 a x és anomenat resta Aquest terme compleix la següent condició d’aproximació És, per tant, un infinitèsim d’ordre superior a x-a n , i pot ésser expresat per qualsevol de les dues maneres següents per a algun t ∈ a,x , per a algun t ∈ a,x En el cas que f n⁺ 1 es pugui integrar en a,x , hom té l’expressió…
atractor
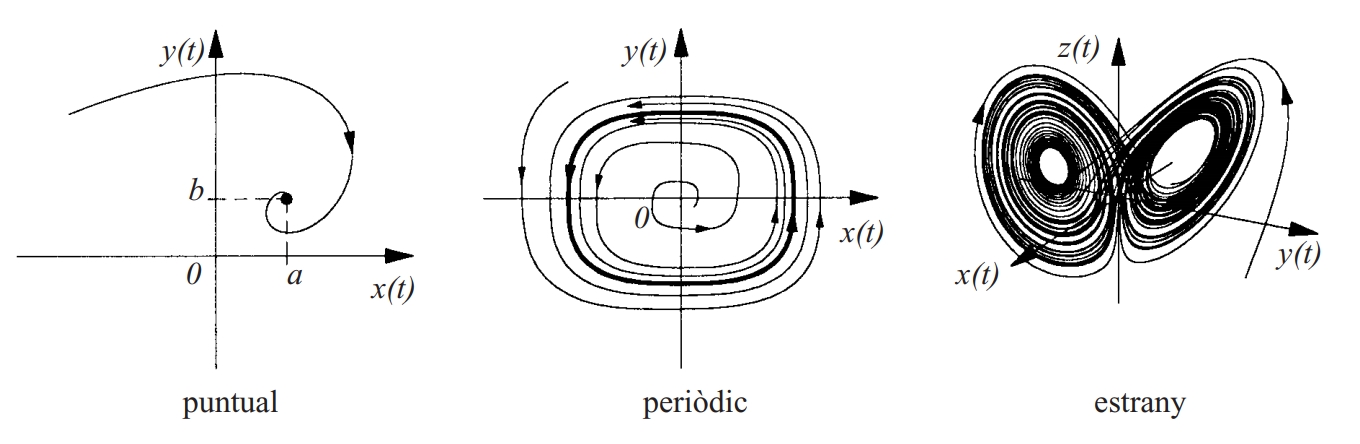
atractors
Matemàtiques
Estat o conjunt d’estats d’equilibri cap als quals convergeix un sistema dinàmic.
Formalment, donada una funció f , és un conjunt tancat E tal que f E és contingut en E , i per a alguns elements x d’un cert conjunt que conté E , la distància de f n E a E tendeix a zero quan n tendeix a infinit Normalment es requereix que l’òrbita de f sigui densa en E per a algun valor de x Si l’atractor E és un fractal es diu que és un conjunt estrany
Diofant d’Alexandria
Matemàtiques
Matemàtic grec.
Els seus escrits sobre àlgebra, amb un estil d’exposició marcadament analític que el vincula estretament amb els treballs dels babilonis, contribuïren de forma essencial al perfeccionament de la notació algèbrica i a l’establiment de noves vies d’investigació En la seva obra cabdal, Aritmètica , estudià una àmplia sèrie de problemes numèrics limitant-se, en general, a trobar-hi solucions particulars mitjançant algun mètode de càlcul i admetent només com a solucions els nombres enters i racionals positius La seva obra influí en el posterior desenvolupament de la geometria…
punt adherent
Matemàtiques
Donat un conjunt A d’un espai topològic, punt x tal que qualsevol entorn de x conté algun punt de A
.
combinació
Matemàtiques
Configuració on hom només té en compte la distinció entre els elements agrupats i no l’ordre en què són presos.
Hom anomena combinació d’ordre n , formada a partir d’un conjunt de m elements 0 ≤ n≤ m, qualsevol dels subconjunts formats en considerar n elements diferents entre els m que integren el conjunt donat, sense tenir-ne en compte l’ordre hom considera, doncs, que dues combinacions són distintes quan algun de llurs elements és diferent El nombre de combinacions d’ordre n , formades a partir d’un conjunt amb m elements, és donat per l’expressió on V n m indica el nombre de variacions, i P n el de permutacions Hom representa sovint C n m per n m , parlant, en aquest, cas, de nombres…
fitat | fitada
Matemàtiques
Dit dels subconjunts, les successions, les funcions, etc que no prenen valors infinits.
Un subconjunt B d’un conjunt ordenat A ,≤ s’anomena fitat inferiorment en A si existeix algun element k ∈ A dit fita inferior de B tal que k ≤ x per a tot x ∈ B Anàlogament, si existeix un element k´∈A tal que x ≤k´ per tot x∈B , hom diu que B està fitat superiorment en A i que k´ és una fita superior de B Un subconjunt s’anomena fitat si ho està inferiorment i superiorment Aquest concepte s’estén de manera natural a successions i funcions, sempre en el context dels conjunts ordenats i es manté la terminologia emprada Així, una successió s’anomena fitada si el conjunt dels…
problema de les paraules
Matemàtiques
Problema d'àlgebra.
D’una banda si hom disposa d’un alfabet finit OOO = {a 1 ,,a n } i, per concatenació, construeix els mots M = ζ 1 ζ r , on cada símbol ζ i és una de les lletres a j ∈ OOO d’aquest alfabet i r ∈ ℕ si, d’altra banda, hom disposa d’un cert diccionari que estableix l’equivalència de certes parelles de mots i, finalment, hom accepta el fet que, en substituir en un mot M = M 1 mM 2 un cert sumbmot m per un altre mot m´ equivalent, obté un mot equivalent M´ = M 1 m' M 2 Cal plantejar la pregunta següent donats dos mots arbitraris M i N , hi ha algun algorisme que permeti de decidir si…
integral impròpia
Matemàtiques
Integral que, a causa de no ésser definida o fitada, la funció a integrar, en algun punt del seu domini de definició, no és calculable directament.
Així, quan la funció f no és definida o fitada a un punt c del seu domini de definició a,b , hom defineix la integral impròpia de f en a,b per si aquests dos límits existeixen, la integral és anomenada convergent i, en cas contrari, divergent Un altre cas d’integral impròpia s’esdevé quan un dels límits d’integració és infinit la integral és definida aleshores, segons el cas, per Les integrals impròpies són també anomenades integrals generalitzades