Resultats de la cerca
Es mostren 8 resultats
dependència algèbrica
Matemàtiques
Relació jeràrquica entre les estructures numèriques.
Per exemple, un subconjunt A del conjunt dels nombres complexos ℂdepèn algèbricament del conjunt dels nombres reals ℝ, si els seus elements poden ésser arrels d’un polinomi amb coeficients en ℝ anàlogament, una part de R pot dependre algèbricament de ℚ En ℝ, els nombres que no depenen algèbricament de ℚ, essent-ne doncs algèbricament independents, són anomenats nombres transcendents així doncs, els nombres transcendents, com e o π, no són arrels de cap polinomi amb coeficients en ℚ
fitat | fitada
Matemàtiques
Dit dels subconjunts, les successions, les funcions, etc que no prenen valors infinits.
Un subconjunt B d’un conjunt ordenat A ,≤ s’anomena fitat inferiorment en A si existeix algun element k ∈ A dit fita inferior de B tal que k ≤ x per a tot x ∈ B Anàlogament, si existeix un element k´∈A tal que x ≤k´ per tot x∈B , hom diu que B està fitat superiorment en A i que k´ és una fita superior de B Un subconjunt s’anomena fitat si ho està inferiorment i superiorment Aquest concepte s’estén de manera natural a successions i funcions, sempre en el context dels conjunts ordenats i es manté la terminologia emprada Així, una successió s’anomena fitada si el conjunt dels…
regle de càlcul

Regle de càlcul
(CC0)
Construcció i obres públiques
Matemàtiques
Petit instrument portàtil de fusta, metall, plàstic, etc. que permetia fer càlculs numèrics d’una manera ràpida i amb una certa aproximació raonable.
Consisteix en un regle proveït de diverses escales graduades, que duu, a més, un petit regle també graduat, desplaçable respecte al regle principal mitjançant unes ranures i uns encaixos adequats, i un cursor transparent, també desplaçable, proveït d’una o més ratlles verticals molt fines Totes les escales són logarítmiques, llevat d’alguna d’especial El principi en què es basa el regle de càlcul és la teoria dels logaritmes, de manera que per a multiplicar dos nombres, de fet hom suma dos segments graduats logarítmicament, i la divisió, anàlogament, consisteix a fer la…
àbac

Àbac xinès
© Fototeca.cat
Matemàtiques
Aparell simple de càlcul digital que permet de fer totes les operacions aritmètiques bàsiques.
Consisteix, normalment, en un tauler o marc proveït de filferros parallels, amb boles foradades que corren al llarg d’aquests Cada enfilall representa un lloc decimal unitats, desenes, centenes, etc, i llur nombre pot ésser variable Les operacions s’efectuen canviant de posició unes boles en relació amb les altres, i, amb una manipulació complicada, hom pot aconseguir fins l’extracció d’arrels L’àbac fou usat a l’antic Egipte i probablement a Babilònia, d’on passà a Grècia i a Roma L’àbac romà consistia en una taula amb diverses ranures paralleles per on hom feia córrer pedres o botons, amb…
sistema de coordenades
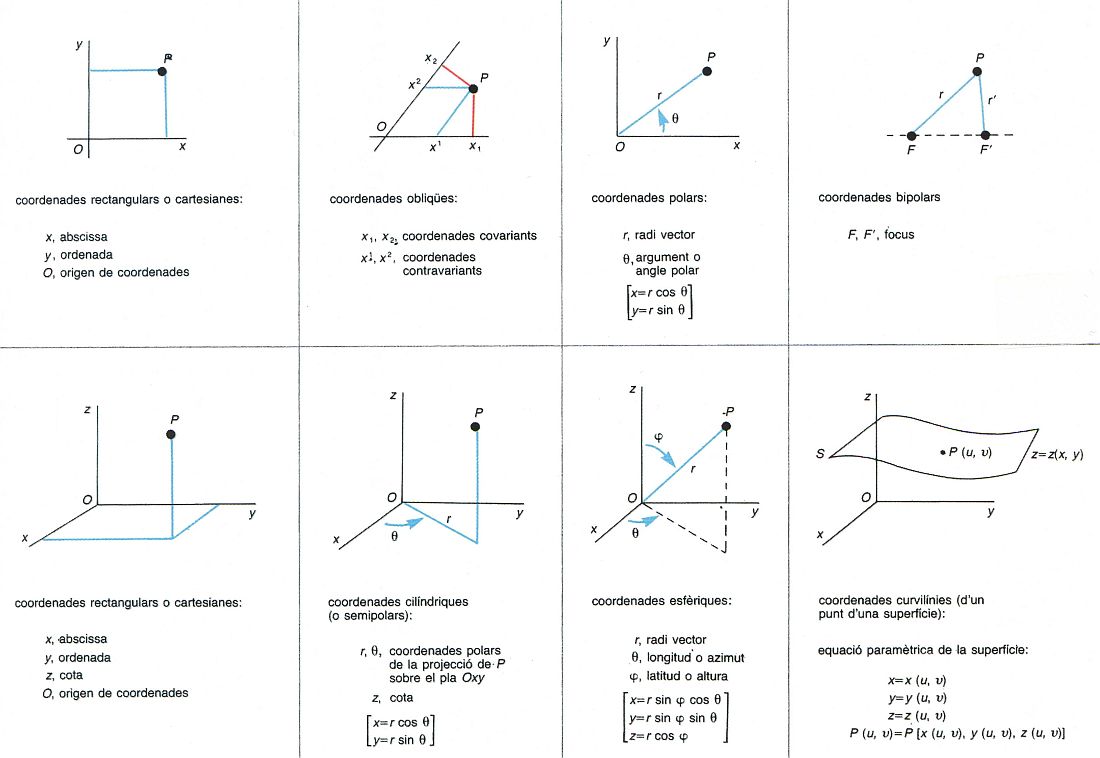
Sistemes de coordenades matemàtiques: coordenades d’un punt del pla (superior) i d’un punt de l’espai (inferior)
©
Matemàtiques
En un cert domini X, conjunt de funcions tal, que els valors en un punt el determinen, de manera que mitjançant un sistema de coordenades cada punt és definit per un conjunt de nombres, que són les coordenades del punt.
Segons els casos les funcions d’un sistema han de complir certes condicions Així, en el pla, un sistema de coordenades lineal consisteix en dues funcions lineals independents Els eixos del sistema són les rectes que corresponen al valor zero de cadascuna de les funcions La intersecció dels dos eixos és l' origen de coordenades Si els eixos són perpendiculars, el sistema és rectangular i les coordenades són rectangulars o cartesianes Si els eixos són oblics, les coordenades són obliqües o rectilínies obliqües En aquest cas, hom pot considerar les coordenades covariants o contravariants , que…
tensor
Física
Matemàtiques
Objecte abstracte que posseeix un determinat sistema de components en cada sistema referencial que hom consideri i tal que, sota transformacions de coordenades, les seves components variïn d’acord amb una transformació predeterminada.
Si E és un espai vectorial de dimensió n sobre un cos algèbric K , hom defineix el tensor covariant d’ordre r com una aplicació T r definida en E x E x r x E = E r , i per a valors en K tal que és lineal en cada component, és a dir, que per a i = 1, 2, 3, , r es compleix a T r x 1 , , x i + y i , , x r = T r x ₁ , , x i ,, x r + T r x 1 , , y i , , x r b T r x ₁ , , λ x i , , x r = λ T r x ₁ , , x i , , x r Els tensors covariants d’ordre 1 formen l’espai E *, anomenat dual de E , és a dir, el conjunt d’aplicacions lineals de E en K E * és, alhora, un espai vectorial de dimensió…
perspectiva

Caprici amb portalada a la vora del llac (segle XVIII-XIX), de Giacomo Guardi (Acadèmia Carrara, Bèrgam)
© Corel
Art
Disseny i arts gràfiques
Matemàtiques
Construcció geomètrica que permet de representar els objectes tridimensionals sobre una superfície bidimensional de forma que, quan és mirada amb un sol ull, immòbil i fixat a la distància justa, la imatge perspectiva coincideix amb la que en donaria la visió directa.
La perspectiva en l’art També hi són inclosos qualssevol mètodes o maneres de representar o suggerir la profunditat espacial sobre el pla pictòric Tot i que des del segle V aC els grecs ja degueren aconseguir algun sistema de formulació perspectiva més o menys plausible, i malgrat, encara, que des dels segles XIII i XIV circulaven, en la tradició dels tallers de pintors d’Itàlia i del nord d’Europa, esquemes geomètrics fragmentaris i fórmules empíriques de reducció perspectiva d’objectes aïllats o de plans parcials, només amb l’humanisme florentí s’obrí camí la perspectiva artificialis o la…
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres naturals La…