Resultats de la cerca
Es mostren 16 resultats
tensor
Física
Matemàtiques
Objecte abstracte que posseeix un determinat sistema de components en cada sistema referencial que hom consideri i tal que, sota transformacions de coordenades, les seves components variïn d’acord amb una transformació predeterminada.
Si E és un espai vectorial de dimensió n sobre un cos algèbric K , hom defineix el tensor covariant d’ordre r com una aplicació T r definida en E x E x r x E = E r , i per a valors en K tal que és lineal en cada component, és a dir, que per a i = 1, 2, 3, , r es compleix a T r x 1 , , x i + y i , , x r = T r x ₁ , , x i ,, x r + T r x 1 , , y i , , x r b T r x ₁ , , λ x i , , x r = λ T r x ₁ , , x i , , x r Els tensors covariants d’ordre 1 formen l’espai E *, anomenat dual de E , és a dir, el conjunt d’aplicacions lineals de E en K E * és, alhora, un espai vectorial de dimensió…
covariant
Matemàtiques
Dit dels tensors d’ordre superior a 1 les components dels quals es transformen, en un canvi de coordenades, segons la matriu del canvi de base.
Per exemple, si és un canvi de base de l’espai vectorial en qüestió, les components d’un vector v covariant es transformen com Les components o coordenandes d’un vector covariant són indexades mitjançant subíndexs v μ
contravariant
Matemàtiques
Dit dels tensors d’ordre superior a 1 les components dels quals es transformen, en un canvi de coordenades, segons la matriu inversa del canvi de base.
Per exemple, si e ' v = A µ v e µ és un canvi de base de l’espai vectorial en qüestió, les components d’un vector v contravariant es transformen com v ' µ = A - 1 µ v v Les components o coordenades d’un vector contravariant són indexades mitjançant superíndexs v µsup
vector
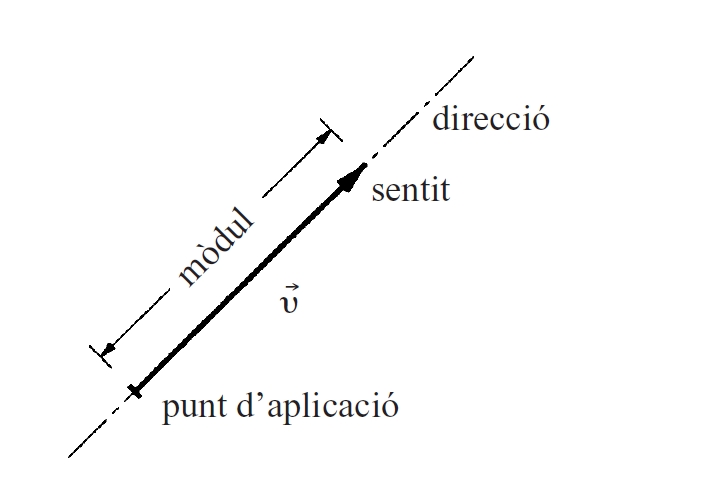
Vector
Física
Matemàtiques
Element d’un espai vectorial.
Des del punt de vista geomètric, a tot vector se li pot associar direcció, mòdul i sentit, i un punt d’aplicació Segons les seves posicions relatives, es parla de vectors simètrics, oposats, conjugats, ortogonals, etc Fixada una base de vectors e 1 ,, e n en un espai vectorial E de dimensió n base d’un espai vectorial, tot vector x de E pot ésser expressat en forma única com a combinació lineal dels elements de la base x = x 1 e 1 + + x n e n Així, x resta determinat pels nombres x 1 , x 2 ,, x n , els quals són dits components de x hom ho escriu x = x 1 ,, x n Si en E hom…
divergència
Matemàtiques
Operador diferencial.
Aquest assigna a una funció vectorial V x la quantitat escalar on V x , V y i V z són les components de V x Hom representa també div V per ∇ V
component connexa
Matemàtiques
En un espai topològic, subespai connex
.
Sigui un punt x d’un espai topològic , és la unió de tots els subconjunts connexos de X que contenen x Les components connexes són sempre tancades i, si són diferents són disjuntives
anàlisi de la variància
Matemàtiques
Qualsevol de les tècniques utilitzades per a determinar la variància observada entre diferents conjunts de dades, especialment per a determinar si les diferències entre dues o més mostres poden ser explicades com a variacions degudes a l’atzar dins una mateixa població.
L’anàlisi de la variància és un procediment creat per RA Fisher per a descompondre la variabilitat d’un experiment en components generalment independents que puguin assignar-se a diferents causes, per a avaluar la influència d’aquestes causes en la variable resposta
norma
Matemàtiques
En els espais vectorials de dimensió 1, 2 o 3 (recta, pla, espai ordinari), longitud d’un vector.
Si el vector és determinat per les seves components en un sistema de coordenades ortonormals eixos perpendiculars i unitats iguals sobre cada eix, la norma del vector v = x 1 , x 2 , x 3 és expressada així Per mitjà del producte escalar, és D’aquesta manera la noció de norma s’estén a espais vectorials de dimensió qualsevol, finita o infinita La norma té en tot cas les propietats de la distància, és a dir, és positiva o nulla, només el vector zero té norma nulla, i satisfà la desigualtat triangular,
flux d’un camp vectorial a través d’una superfície
Matemàtiques
Donat un camp vectorial A i una superfície orientable S, integral de superfície de A sobre S
.
El flux elemental de A a través d’un element de superfície dS és el producte escalar d ϕ= A d S , on d S és el vector normal a dS i de mòdul dS El flux total de A a través de la superfície S és, doncs, Φ=∫∫ s A d S Si S és una superfície tancada que determina un volum V , la fórmula de Gauss o d’Ostrogadskij afirma que Φ = ∫∫ s A d S = ∫∫∫∂ x A x + ∂ y A y + ∂ z A z dV , on A x , A y i A z són les components del camp A
afix
Matemàtiques
Fent referència a un nombre complex, punt les coordenades del qual són les components del nombre complex.