Resultats de la cerca
Es mostren 16 resultats
polinomis de Bernoulli
Matemàtiques
Polinomis Φn(x) definits pel desenvolupament
En termes dels nombres de Bernoulli s’expressen com Hom empra els polinomis de Bernoulli en fòrmules d' integració numèrica i en càlcul de diferències finites
objecte matemàtic
Matemàtiques
Concepte matemàtic precisat per una definició.
El caràcter matemàtic de l’objecte és donat per la possibilitat d’establir relacions entre aquest i els altres objectes de la teoria, en forma de teoremes, els quals hom dedueix dels axiomes de partença Sovint els objectes matemàtics són classes d’equivalència construïdes a partir d’altres elements anteriors concepte de nombre enter, de direcció, de vector lliure, etc Hom anomena objectes primitius d’una teoria matemàtica aquells que no poden ésser definits a partir d’objectes anteriors i han d’ésser definits establint una sèrie de condicions que els relacionen entre…
definició
Matemàtiques
Introducció d’un nou concepte fent referència a conceptes anteriors ja definits.
Necessàriament hi ha, doncs, conceptes primaris o no definibles, reduïts, en primera aproximació, als conceptes de conjunt, element, i pertinença Hom axiomatitza aquests conceptes primaris per tal d’evitar contradiccions aquest procés constituiex l’objecte de la teoria de conjunts conjunt
nombres de Fermat
Matemàtiques
Nombres, Fn, definits per l’expressió (per a n = 1,2,3,...).
El 1640 Fermat cregué que aquests nombres eren primers, però l’any 1740 Euler donà una descomposició per a F 5 = 4 294 967 297, com a producte de 641 per 6 700 417, i posteriorment hom ha demostrat que per a n tal que 5 ≤n≤17 , F n no és primer, i que d’altres nombres de Fermat, com F 1 9 4 5 , F 3 3 1 0 i F 6 5 3 7 són descomponibles El 1796 Gauss demostrà que els únics polígons regulars que hom pot construir amb regle i compàs són els que tenen un nombre de Fermat de costats
base dual
Matemàtiques
Base definida en un espai vectorial E de dimensió finita.
Si e 1 , e n és una base de E , aleshores el conjunt de formes lineals f i E→K, amb imatges sobre el cos K de l’espai vectorial, definits per f i e j =δ i j , essent δ i j =0 si i ≠ j , δ ij =1, forma una base de l’espai dual E *, i s’anomena la base dual de la inicial
cub
Matemàtiques
Políedre regular format per sis cares quadrades.
Les tres arestes concurrents a cada vèrtex són perpendiculars entre elles en conseqüència, el tríedre format per les tres arestes és trirectangle, els díedres definits per dues cares amb una aresta comuna són rectes, i les cares oposades són paralleles Les quatre diagonals del cub es tallen en un punt, el centre del cub, que és, alhora, el centre de simetria d’aquesta figura Si la longitud de l’aresta del cub és a , el volum del cub val a 3 , i la seva diagonal té una longitud de a √3
conjunt

Representació gràfica de la relació de pertinença i de les operacions d’unió i intersecció dels conjunts
© Fototeca.cat
Matemàtiques
Reunió d’objectes ben definits en la intuïció o en el pensament, considerada com una totalitat (Cantor).
Aquesta definició, des del punt de vista matemàtic, no és vàlida, i, així, en matemàtiques la noció de conjunt no és definida, i s’inclou dins del desenvolupament d’una teoria axiomàtica que eviti les paradoxes i contradiccions com les que, a començament del segle XX, posaren en qüestió no solament la teoria de conjunts, sinó bona part de la matemàtica Hom no defineix, doncs, ni conjunt, ni element, ni la relació de pertinença, i es conforma amb la idea intuïtiva del que signifiquen frases com Un conjunt és format per elements, o l’element 4 pertany al conjunt dels nombres naturals La…
triangle
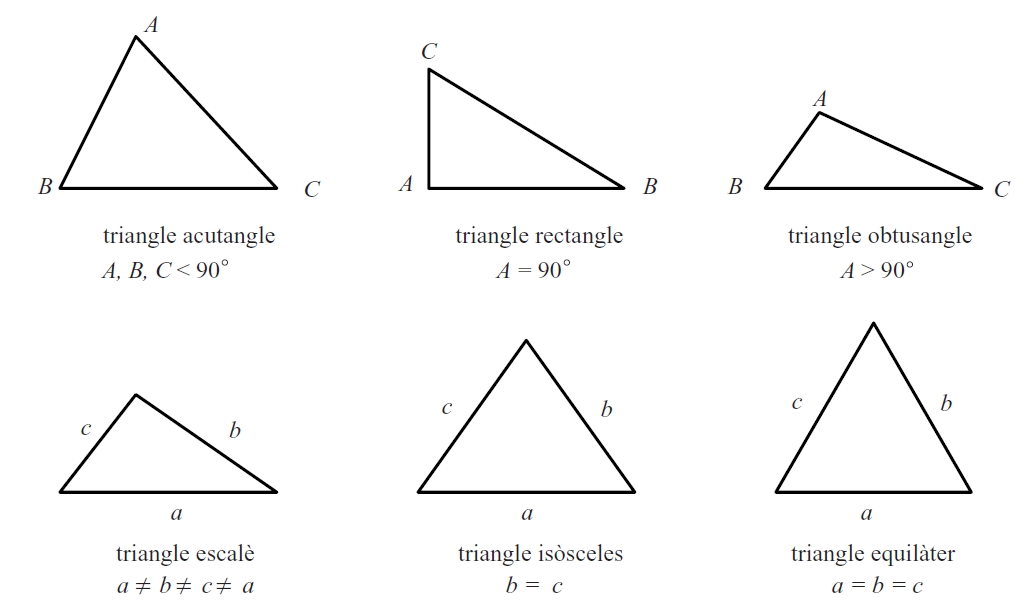
triangles
Matemàtiques
Figura formada en unir tres punts (anomenats vèrtexs) no alineats amb tres segments de línia recta.
Un triangle és anomenat acutangle si els seus angles interiors són aguts, obtusangle si té un angle interior obtús, escalè si cap costat és igual als altres dos, isòsceles si té dos costats iguals, equilàter si té tots tres costats iguals, i rectangle si un dels angles interiors és un angle recte 90° Si no és rectangle és anomenat obliquangle L’àrea d’un triangle és igual a la meitat del producte de la base qualsevol costat per l’altura recta perpendicular des del vèrtex oposat a la base fins a aquesta base La resolució d’un triangle , és a dir, la determinació dels seus angles i costats, a…
intuïcionisme
Matemàtiques
Corrent del pensament matemàtic, nascut a la segona meitat del s XIX.
Propugna que la matemàtica és l’estudi d’uns tipus de construccions mentals en les quals els objectes que hom maneja han d’ésser definits donant un criteri que en permeti la construcció i on el llenguatge emprat, sigui ordinari o simbòlic, només és un instrument auxiliar i no una part essencial de les construccions formalisme Hom accepta que la matemàtica intuïcionista és formada de tot allò que és conseqüència segons les normes de la lògica intuïcionista de la construcció de la successió dels nombres naturals ℕ, de la qual resulten evidents els axiomes de Peano base de la…
moviment
Matemàtiques
Aplicació d’un espai mètric en ell mateix que conserva la distància.
Actualment hom tendeix a anomenar-lo isometria El conjunt de moviments definits sobre un espai, amb l’operació de composició o producte de moviments, constitueix un grup En particular, és interessant l’estudi dels moviments al pla i a l’espai ordinaris El grup dels moviments del pla és generat per les simetries axials, és a dir, tot moviment del pla pot ésser descompost en producte d’un cert nombre de simetries axials Els de nombre parell són anomenats moviments directes , conserven el sentit del pla i són un subgrup del grup de moviments els altres són anomenats moviments…