Resultats de la cerca

Es mostren 14 resultats

dual

Matemàtiques
Dit de dues nocions matemàtiques que, permutades en l’enunciat d’un teorema, donen lloc a un nou teorema.
Per exemple, la intersecció i la unió són duals, ateses les lleis de De Morgan
Gran enciclopèdia catalana

espai dual

Matemàtiques
Conjunt d’aplicacions lineals (formes o funcionals) d’un espai vectorial en el cos sobre el qual és definit.
El lligam entre l’espai E i el seu dual E * és força estret, puix que si E és de dimensió finita, dim E = dim E * , i E * * ≃ E , és a dir, el dual del dual és canònicament isomorf a E En el cas d’un espai vectorial topològic E , hom parla del dual topològic, constituït per les formes contínues de E en el cos base dual
Gran enciclopèdia catalana

base dual

Matemàtiques
Base definida en un espai vectorial E de dimensió finita.
Si e 1 , e n és una base de E , aleshores el conjunt de formes lineals f i E→K, amb imatges sobre el cos K de l’espai vectorial, definits per f i e j =δ i j , essent δ i j =0 si i ≠ j , δ ij  =1, forma una base de l’espai dual E *, i s’anomena la base dual de la inicial
Gran enciclopèdia catalana

espai dual

Matemàtiques
Espai de les formes lineals sobre un espai vectorial .
Gran enciclopèdia catalana

bidual

Matemàtiques
Dit de l’espai dual del dualE* d’un espai vectorial E.
E resulta isomorf al bidual E **, on l’isomorfisme és el que transforma el vector x ∈ E en l’element x ’ E* → K definit per x ’ u = u x, per a tot u ∈ E *
Gran enciclopèdia catalana

semireticle

Matemàtiques
Conjunt ordenat en el qual, donats dos elements, sempre existeix el suprem (element que és el més petit major que els dos donats).
També és possible la definició dual, que exigeix l’existència d’un ínfim
Gran enciclopèdia catalana

teorema de Pascal

Teorema de Pascal

© fototeca.cat

Matemàtiques
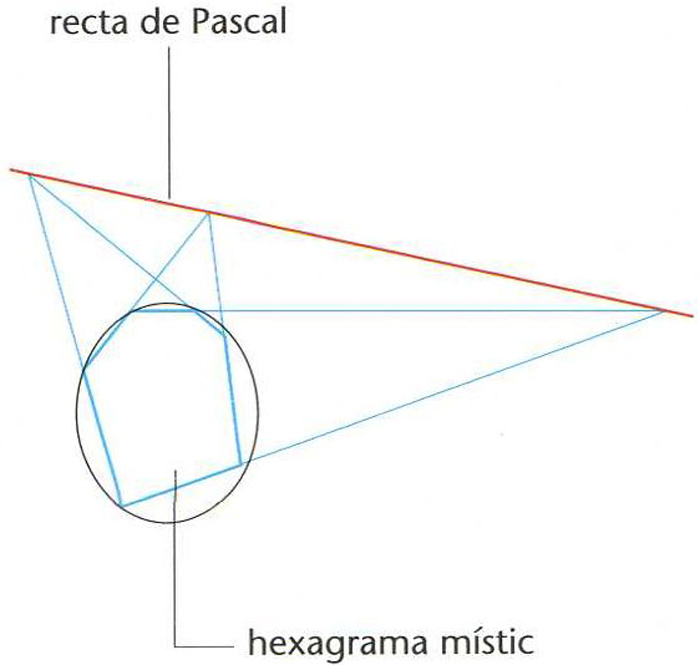
Teorema segons el qual els tres punts d’intersecció dels costats oposats d’un hexàgon inscrit en una cònica determinen una recta anomenada recta de Pascal.
L’hexagram format és anomenat hexagram místic El dual d’aquest teorema és el teorema de Brianchon
Gran enciclopèdia catalana

teorema de Brianchon

Teorema de Brianchon

© fototeca.cat

Matemàtiques
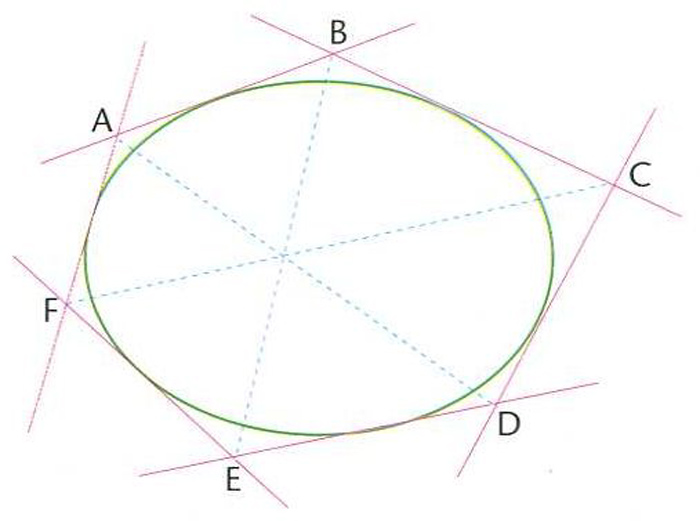
Teorema segons el qual si un hexàgon té els costats tangents a una cònica, aleshores tres de les seves diagonals són concurrents.
Un hexàgon d’aquest tipus s’anomena un hexàgon de Brianchon , i el punt de concurrència s’anomena punt de Brianchon Aquest teorema és el dual del teorema de Pascal
Gran enciclopèdia catalana

teorema de Menelau

teorema de Menelau

© fototeca.cat

Matemàtiques
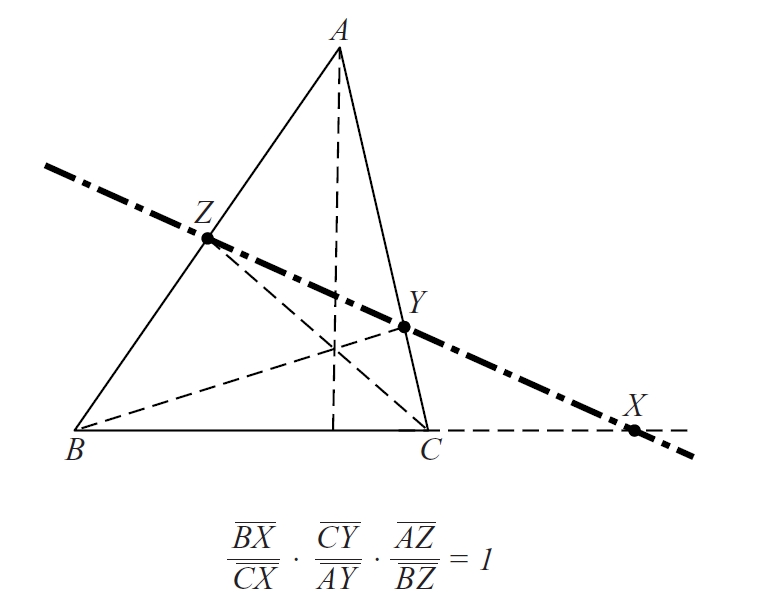
Teorema segons el qual tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB, respectivament, d’un triangle ABC, estan alineats si, i solament si, (BX⁄CX)·(CY⁄AY)·(AZ ⁄ BZ) = 1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui +1 X , A , B Y , B , C Z , C , A = 1 Aquest teorema és dual del teorema de Ceva
Gran enciclopèdia catalana

teorema de Ceva

teorema de Ceva

Matemàtiques
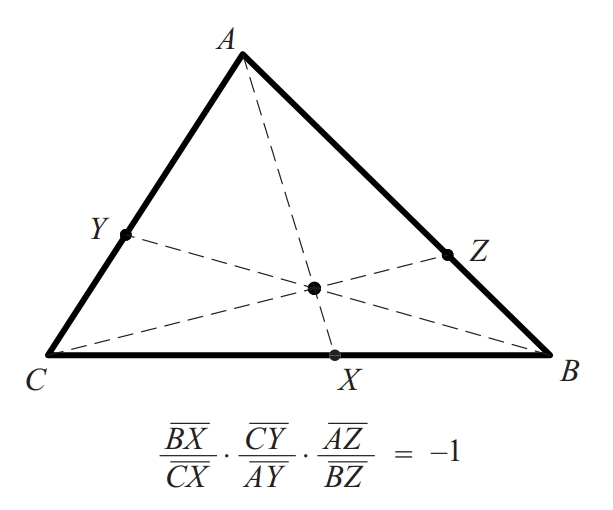
Teorema segons el qual, prenent tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB d’un triangle de vèrtexs A, B i C, les rectes AX, BY i CZ són concurrents si, i solament si, (BX ⁄ CX) · (CY ⁄ AY) · (AZ ⁄ BZ) = –1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui –1 X , A , B Y , B , C Z , C , A = –1 Aquest teorema és dual del teorema de Menelau
Gran enciclopèdia catalana