Resultats de la cerca
Es mostren 11 resultats
freqüència
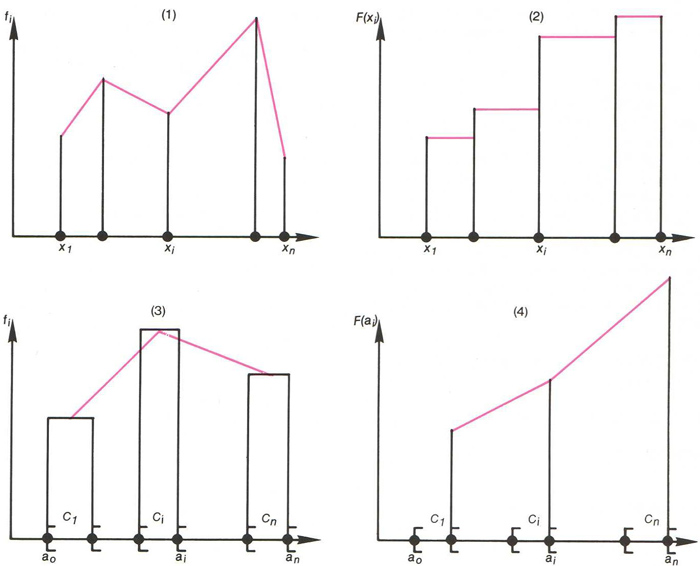
Representacions gràfiques de la freqüència d’una distribució estadística: si el caràcter quantitatiu és discret, (1) és el seu polígon de freqüencies i (2) és la seva corba cumulativa; si el caràcter quantitatiu és continu, (3) és el seu polígon de freqüències i (4) és la seva corba cumulativa
© Fototeca.cat
Matemàtiques
En una distribució estadística d’un caràcter quantitatiu, quocient entre l’efectiu d’un valor concret del caràcter, o d’una classe de valors, i el nombre d’individus que integren la mostra.
Si el caràcter quantitatiu és discret , i pren els valors x 1 ,,x n sobre una mostra de N individus, la freqüència o freqüència relativa del valor x i és el quocient f i = n i / N , on n i és l’ efectiu del valor x i és a dir, el nombre d’individus de la mostra que presenten el valor x i del caràcter La representació gràfica de la funció de distribució x i → f i és una línia poligonal obtinguda en unir els punts de coordenades x i , f i , i =1,, n , anomenada polígon de freqüències Si el caràcter quantitatiu és continu , donada una classe o interval C i = a i - 1 , a i del…
prova de khi quadrat
Matemàtiques
Prova de significació emprada per a sèries grans d’observacions, que mesura l’acostament entre la distribució de les dites observacions i una distribució de freqüències teòricament establerta, dita de χ 2
.
Si F i designa les freqüències experimentals i P i les freqüències esperades teòricament, hom calcula la fidelitat de la distribució experimental envers la de χ 2 per mitjà de la fórmula χ 2 =0 en el cas de coincidència entre totes dues distribucions Hom sol emprar aquesta prova per al contrast d’hipòtesis, amb uns marges de fiabilitat del 95 o del 99%, i és aplicable a situacions molt diverses
freqüència cumulativa
Matemàtiques
En una distribució estadística d’un caràcter quantitatiu, suma de les freqüències dels valors del caràcter, o de les classes de valors del caràcter, anteriors al valor que caracteritza la freqüència cumulativa en qüestió.
Si el caràcter quantitatiu és discret , i pren els valors x 1 ,, x n , la freqüència cumulativa del valor x i és el nombre on f j és la freqüència del valor x j La representació gràfica de la funció x i → F x i és una corba esglaonada anomenada corba cumulativa o corba de freqüències cumulatives Si el caràcter quantitatiu és continu , donada una classe o interval C i = a i - 1 , a i del conjunt de valors del caràcter, la freqüència cumulativa del valor a i o de la classe C i és el nombre on f j és la freqüència de la classe C j La representació gràfica de la funció a i → F…
mitjana
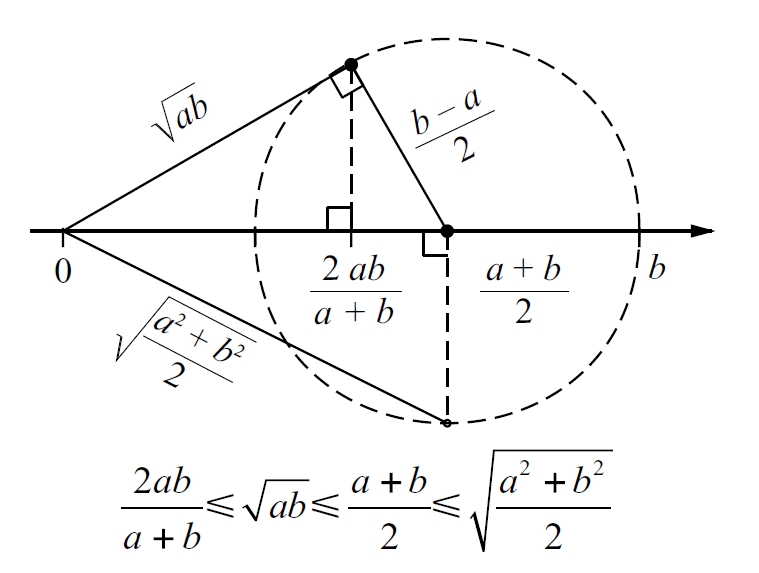
Mitjanes dels nombres a i b: harmònica, geomètrica, aritmètica i quadràtica
© fototeca.cat
Matemàtiques
Donats n valors o observacions x1, x2, ..., xn, valor x definit com la suma de tots ells dividida per llur nombre, és a dir, .
La mitjana x així definida és anomenada també mitjana aritmètica i valor mitjà Si les observacions constitueixen el conjunt de la població, x serà la mitjana de la població , mentre que si les observacions són d’una mostra aleatòria de la població mostreig, x és la mitjana de la mostra A la pràctica, la mitjana de la població és normalment desconeguda, i hom utilitza com a estimació la mitjana d’una mostra Quan les observacions poden ésser agrupades en k classes, amb efectius respectius n 1 , n 2 , , n k i freqüències respectives f 1 , f 2 , , f k , la fórmula per al càlcul de…
moment
Matemàtiques
Donada una variable aleatòria X, i f (x) essent la seva funció de densitat, valor mr donat per la fórmula
on a és un nombre real fixat i r és un nombre natural que determina l’ordre del moment.
Normalment hom escull com a valor de a el de l’esperança matemàtica de X , en el qual cas el moment de primer ordre és a dir r = 1 és nul i el de segon ordre és a dir, r = 2 coincideix amb la variància A partir dels moments, mitjançant l’anomenat mètode dels moments , hom pot estimar els paràmetres que caracteritzen una distribució de freqüències obtinguda a partir de l’observació d’una mostra
error
Física
Matemàtiques
Diferència entre el resultat de la mesura experimental d’una magnitud i el seu valor real (error absolut).
Els errors són de dos tipus sistemàtics , que procedeixen d’imperfeccions en les escales dels aparells de mesura i que poden ésser reduïts comprovant prèviament els calibratges, i accidentals , que són deguts a les limitacions naturals dels sentits de l’observador, sobretot de la vista i l’oïda Per a acotar-los hom repeteix una mesura diverses vegades Els valors mesurats x i presenten una desviació entorn del valor mitjà, x m , que hom pren com a millor valor Si hom dibuixa la gràfica de les desviacions en funció de les freqüències, obté la corba de campana o de Gauss , en la…
histograma
Matemàtiques
Representació gràfica, formada per rectangles, de les freqüències d’una variable.
Quan la variable pren valors discrets, tots els rectangles tenen la mateixa amplada i llur altura és proporcional a la freqüència corresponent al punt on el rectangle és situat Quan la variable és contínua, els rectangles són contigus i l’àrea de cadascun d’ells, que té per base un cert interval de la variable, és proporcional al valor global de la freqüència corresponent a l’interval
anàlisi de Fourier
Física
Matemàtiques
Estudi de les funcions que té per finalitat d’expressar-les mitjançant una sèrie o una integral en què intervenen les funcions trigonomètriques.
El fonament d’aquesta tècnica matemàtica és l’anomenat, de vegades, teorema de Fourier Tota funció periòdica f x , contínua o, com a màxim, amb un nombre finit de discontinuïtats finites, pot expressar-se mitjançant una sèrie trigonomètrica, de la següent manera la sèrie que apareix en aquesta expressió és la sèrie de Fourier de o associada a la funció f x El nombre ω és la pulsació fonamental de la sèrie de Fourier de f i és igual a la pulsació o freqüència angular de f , és a dir, ω=2π/ T , on T és el període de f El primer terme de la sèrie de Fourier de f , terme que correspon al…
Daniel Bernoulli
Biologia
Física
Matemàtiques
Físic, matemàtic i fisiòleg neerlandès.
Fill i nebot de matemàtics, s’inicià en la disciplina en la qual sobresortiren els seus antecessors, però aviat es decantà vers les ciències experimentals Després de fer estudis de medicina a Basilea, Heidelberg i Estrasburg es doctorà en aquests camp a vint-i-un anys, el 1724 publicà les Exercitationes quaedam mathematicae , que reflectien el seu interès per la matemàtica i en les quals tractava temes de probabilitat i la resolució de l’equació diferencial de Riccati Fou cridat a l’Acadèmia de Sant Petersburg on romangué del 1725 al 1733 Fou aquest el període més fèrtil de la seva creació hi…
,
prova khi quadrat de Pearson
Matemàtiques
Prova khi quadrat que mesura la distància entre una distribució de freqüències observada i una altra de predita amb un model estadístic determinat.
És la prova khi quadrat més utilitzada