Resultats de la cerca
Es mostren 59 resultats
límit d’una successió
Matemàtiques
Valor al qual una successió s’acosta més i més (tant com hom vulgui).
Donada una successió { a n }, a 1 ,, a n ,, hom diu que el límit de la successió és A , o que la successió tendeix a a , si per a tot real ε > 0, per petit que sigui, existeix un terme a m de la successió tal que si n > m aleshores | A-a n |
teorema central del límit
Matemàtiques
Teorema segons el qual, per a una distribució de probabilitat arbitrària de mitjana μ i variància σ2, i essent x̄ la mitjana de n observacions independents d’aquesta distribució, la variable
té una distribució
.
Segons aquest teorema, per a n → ∞ la mitjana de n observacions independents segueix una llei normal de mitjana igual a la de la població i de variància igual a 1/ n de la d’aquesta A la pràctica, per a n ≥ 10 l’aproximació és ja suficient Aquest teorema, formulat per Lindeberg i Levi, és un dels més importants de la teoria de probabilitats De Moivre en feu la primera demostració el 1732 en el cas d’una distribució binomial, i posteriorment Ljapunov en demostrà la validesa molt general en cas de variables aleatòries Això explica per què a la pràctica hi ha moltes variables que segueixen una…
límit d’una funció en un punt
Matemàtiques
Valor al qual tendeix la variable dependent de la funció quan la variable independent tendeix al valor del punt en qüestió.
Donada una funció fD ⊂ ℝ → ℝ i un punt del seu domini de definició, a ∈ D , hom diu que el límit de f quan x tendeix a a és λ, o que f tendeix a λ quan x tendeix a a , si per a tot real ε> 0, per petit que sigui, existeix un real δ> 0 tal que si | x-a | 0 tal que si | x - a | A
funció reglada
Matemàtiques
Funció f:[a,b]⊂ℝ→ℝtal que admet un límit a l’esquerra en tot punt de l’interval (a,b] i un límit a la dreta a tot punt de l’interval [a,b)
.
Hom diu aleshores que f és reglada sobre l’interval a,b Una funció f és reglada sobre a,b si i només si és el límit uniforme d’una successió de funcions esglaonades en a,b
criteri de Cauchy
Matemàtiques
Criteri de convergència o divergència d’una sèrie infinita segons el qual la sèrie convergeix si, a partir d’un cert terme, el límit del valor absolut de l’arrel enèsima del terme general, quan n tendeix a infinit, és menor que la unitat.
Si aquest límit és major que la unitat, la sèrie és divergent, i si el límit és igual a la unitat, aquest criteri no decideix Encara que menys còmode, aquest criteri és més potent que el criteri de D'Alembert
anàlisi matemàtica

anàlisi matemàtica Portada dels Philosophiae Naturalis Principia Mathematica de Newton (1687)
© Fototeca.cat
Matemàtiques
Part de les matemàtiques bastida sobre els conceptes bàsics de funció, límit, continuïtat, derivada i integral.
És el desenvolupament modern del càlcul infinitesimal, elaborat durant els segles XVII i XVIII, que tenia com a principals problemes el de les quadratures determinació de la longitud d’una corba i de les àrees i volums de figures i el de la tangència traçat de tangents a corbes i superfícies Els coneixements que s’anaren acumulant sobre aquests temes formaren els càlculs integral i diferencial, cor d’aquesta disciplina matemàtica L’anàlisi matemàtica presenta els trets distintius de l’abstracció i generalitat dels seus mètodes, característics del rigor del raonament lògic És el resultat d’una…
derivada direccional d’una funció en un punt
Matemàtiques
Donada una funció D ⊂ℝ n →ℝ, un punt a∈D, i un vector no nul v∈ℝ n , límit, si existeix, del quocient [f( a+h v) - f( a)]/h, quan h tendeix a zero.
Si aquest límit existeix hom el nota per f ´ a , v , i hom diu que f és derivable en la direcció v en el punt a i que f ´ a , v és la derivada de f en la direcció en el punt a Les derivades parcials són derivades en la direcció dels vectors unitaris canònics de ℝ n
derivada d’una funció en un punt
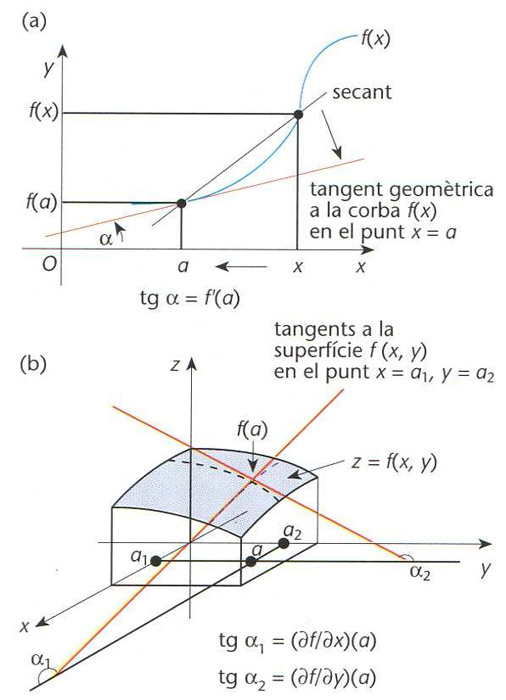
Interpretació gràfica de la derivada d’una funció (a) i de les derivades parcials d’una funció de dues variables (b); en (a), tgα = f' (a); en (b), tgα1 = ϑf/ϑx (a) i tgα2 = ϑf/ϑy (a)
© fototeca.cat
Matemàtiques
Donada una funció f: D⊂ℝ→ℝ i un punt del seu domini de definició, a ∈D, límit, si existeix del quocient [f(x) — f(a)]/(x-a) quan x tendeix a a tot mantenint-se a l’interior de D.
Quan aquest límit existeix, hom diu que la funció f és derivable en a , i el límit és notat per f´ a , df/dx a o Df a , i hom l’anomena derivada de f en el punt a Hom diu que f és derivable en un cert domini S si ho és a cada punt de S Aleshores, la funció f´ x que assigna a cada punt a ∈ S la derivada de f en a és anomenada funció derivada de f o, simplement, derivada de f Si f´ x és, al seu torn, derivable en un cert domini T , hom pot definir-n'hi la derivada, que és la derivada segona de f, f´´ x Hom procedeix consecutivament per tal de definir les…
successió
Matemàtiques
Conjunt d’elements ordenats seguint l’ordre dels nombres naturals ℕ, és a dir, família d’elements (an ) indexats amb nombres naturals.
Així, 1/2, 1/3, , 1/ n , i x , 2 x 2 , 3 x 3 , , nx n , són successions Hi ha també successions de funcions, de variables aleatòries, etc Tota successió, anomenada també seqüència , pot ésser finita a 1 , a 2 , , a n o infinita a 1 , a 2 , , a n , El terme a n és dit terme n-èsim enèsim o terme general Donar una successió infinita pressuposa donar aquest terme general, és a dir, una llei de recurrència Un punt P és dit punt d’acumulació d’una successió a n , si en tot entorn de P hi ha infinits termes de la successió La successió 1, 1/2, 1, 1/3, , 1, 1/ n , té dos punts d’acumulació…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- Pàgina següent
- Última pàgina