Resultats de la cerca
Es mostren 15 resultats
trajectòria
Matemàtiques
Corba que talla amb la mateixa inclinació totes les corbes d’un feix o sistema donat.
Són dites trajectòries ortogonals si les tallen en un angle recte
vector
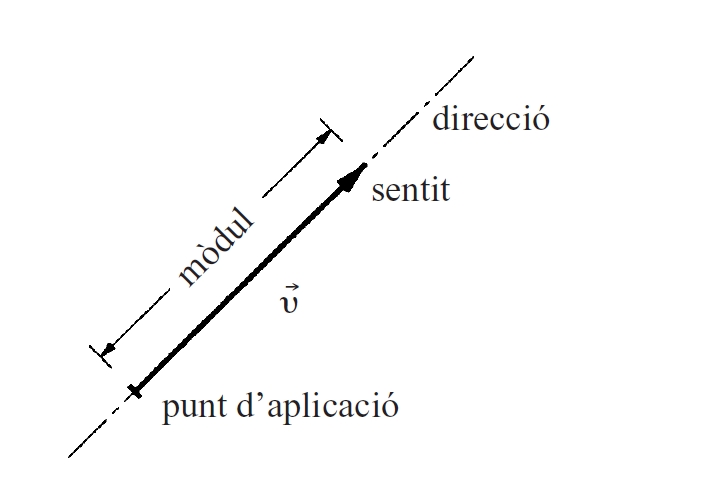
Vector
Física
Matemàtiques
Element d’un espai vectorial.
Des del punt de vista geomètric, a tot vector se li pot associar direcció, mòdul i sentit, i un punt d’aplicació Segons les seves posicions relatives, es parla de vectors simètrics, oposats, conjugats, ortogonals, etc Fixada una base de vectors e 1 ,, e n en un espai vectorial E de dimensió n base d’un espai vectorial, tot vector x de E pot ésser expressat en forma única com a combinació lineal dels elements de la base x = x 1 e 1 + + x n e n Així, x resta determinat pels nombres x 1 , x 2 ,, x n , els quals són dits components de x hom ho escriu x = x 1 ,, x n Si en E hom defineix un…
coordenades cartesianes
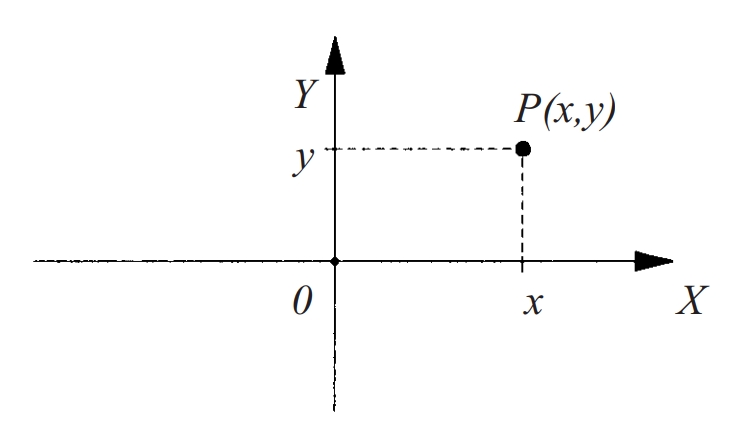
coordenades cartesianes al pla
Matemàtiques
En un espai euclidià, coordenades afins respecte d’una referència afí.
En el cas d’una referència, es diu que les coordenades són cartesianes rectangulars Així, tot punt del pla espai P s’identifica amb les seves coordenades x , y x , y , z on cada coordenada representa la projecció de P en l’eix corresponent d’acord amb la direcció dels altres eixos També s’usen referències no ortogonals coordenades cartesianes a l’espai
Jean Gaston Darboux
Matemàtiques
Matemàtic francès.
La major part dels seus treballs es desenvoluparen en el camp de la geometria Publicà memòries sobre l’estudi de les superfícies ortogonals 1864-66, equacions diferencials de segon ordre en derivades parcials 1870 —per a les quals proposà un nou mètode d’integració—, aproximació de funcions, funcions discontínues, etc Una de les seves obres més importants, Leçon sur la théorie générale des surfaces et les applications géométriques du calcul infinitésimal 4 volums, 1887-96, constitueix una síntesi dels treballs duts a terme en els camps de la geometria i del càlcul durant el s XIX…
factor
Matemàtiques
Psicologia
Cadascuna de les variables causals, de vegades no directament mesurables, que influeixen o poden influir sobre un resultat mesurable.
Quan els factors són directament mesurables, hom en fa l’estudi mitjançant plans d’experiències factorials i l’anàlisi de la variància , quan no són directament mesurables, mitjançant l’anàlisi factorial En aquest cas hom distingeix entre els factors comuns quan influeixen sobre la realització de diverses variables observables i els factors específics quan influeixen només sobre la realització d’una variable observable En l’aplicació de l’anàlisi factorial als estudis psicològics, Spearman considerà un sol factor comú, que anomenà general g , i establí la teoria dels dos factors el general i…
axonometria
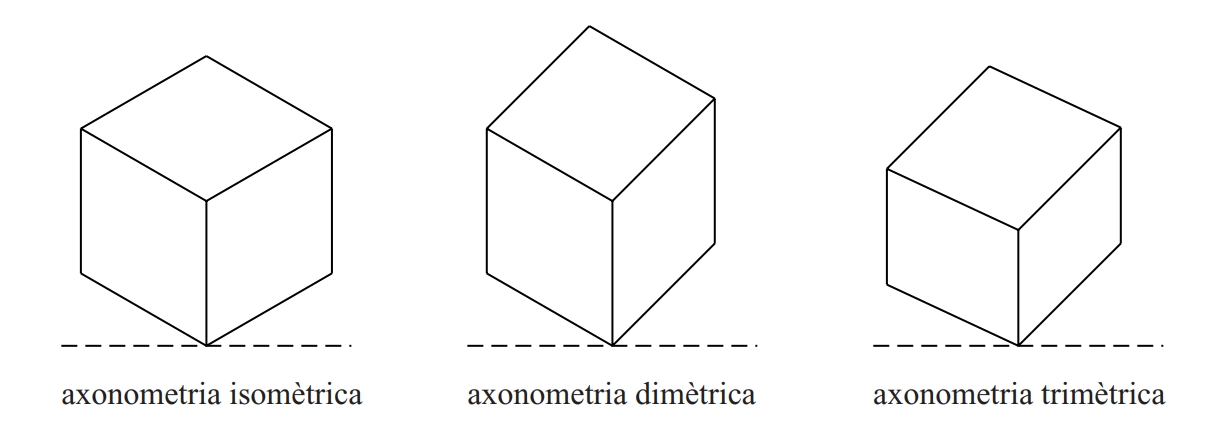
axonometria
© Fototeca.cat
Matemàtiques
Mètode de representació de les figures de l’espai.
En aquest sistema hom pren un tríedre trirectangle com a referència i determina cada punt de l’espai per les seves projeccions ortogonals damunt els plans del tríedre Després hom projecta sobre el pla del dibuix la figura formada pel tríedre, el punt i les seves projeccions sobre els plans del tríedre És útil, per a fixar bé la posició de la figura a l’espai, de dibuixar les interseccions dels plans del tríedre amb el pla de dibuix Aquestes rectes d’intersecció són anomenades traces Projecció axonomètrica d’un cub © Fototecacat Per a determinar les projeccions d’un punt convé de…
ortografia
Disseny i arts gràfiques
Matemàtiques
Tècnica de la geometria projectiva consistent a fer projeccions ortogonals en un pla vertical.
evolvent
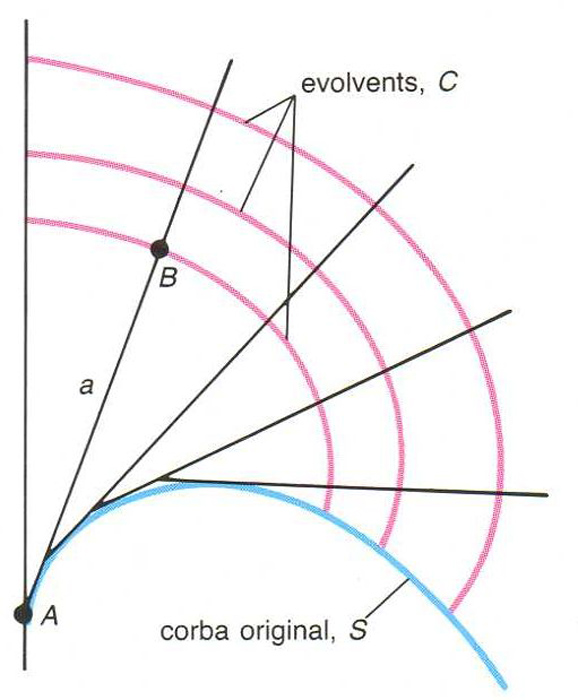
Les corbes C són les evovlents de S
© fototeca.cat
Matemàtiques
Donada una corba S
, cadascuna de les corbes ortogonals a les tangents de S
.
Si C és una envolvent de S , S és l'evoluta C Donada la corba S , hom pot generar una evolvent tot fixant una tangent a S en un punt de tangència A , limitant-ne la seva longitud a i anant-la enrotllant a la corba, de manera que el punt extrem B determina una evolvent Les diferents longituds a determinen les diferents evolvents
grup ortogonal
Matemàtiques
Matrius ortogonals que formen un subgrup O(n K) del grup lineal GL n(K).
base ortonormal
Matemàtiques
Base d’un espai vectorial euclidià formada per vectors que són ortogonals dos a dos.
Per exemple, a ℝ n la base canònica és ortonormal respecte al producte escalar