Resultats de la cerca
Es mostren 87 resultats
logaritme augmentat
Matemàtiques
Logaritme decimal d’un nombre menor que 1, a la característica del qual, que és negativa, hom ha aplicat cert artifici per tal que sigui sempre positiva.
L’artifici consisteix a sumar a la característica el nombre de desenes positives que calgui per tal que sigui positiva, tot posant aquest nombre de desenes com a superíndex de la característica superíndex que hom anomena augment Així, hom substitueix la característica negativa a per 10 n - a n , n essent un nombre enter positiu tal que 10 n > ¦ a ¦ Els logaritmes augmentats foren ideats per tal de disminuir les probabilitats d’error en les operacions amb logaritmes en certs tipus de càlculs, com en els de navegació astronòmica, artilleria, topografia, etc
teorema de Bernoulli
Matemàtiques
Donat un nombre ε arbitràriament petit, la probabilitat que la diferència entre la freqüència relaiva f de l’esdeveniment favorable en una sèrie de proves i la probabilitat p d’aquest esdeveniment sigui, en valor absolut, superior a ε tendeix a zero en augmentar indefinidament el nombre de proves.
O sigui Aquest teorema fa aparèixer el lligam que hi ha entre freqüència relativa i probabilitat, la qual és el valor mitjà de la freqüència per a un nombre molt gran de proves Com que hi intervé un nombre de proves tant gros, aquest teorema és conegut també amb el nom de llei dels grans nombres
funció harmònica
Matemàtiques
Funció f:ℝ n →ℝque és solució de l’equació de Laplace, és a dir que satisfà Δf≡∇2 f=∂2 f/∂x1 2 +...+∂2 f/∂xn 2 =0.
A més a més hom exigeix, generalment, que f sigui definida en un obert U ⊂ℝ n que hi sigui contínuament diferenciable dues vegades
trivial
Matemàtiques
Dit de la solució formada per zeros, en un sistema d’equacions que sigui homogeni.
superfície desenvolupable
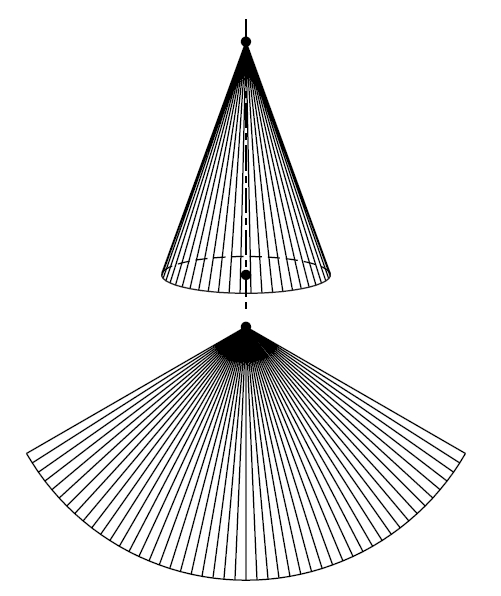
Superfície desenvolupable i el seu desenvolupament
Matemàtiques
Superfície isomètrica al pla, és a dir, que hom pot desplegar sense deformació sobre un pla.
Perquè una superfície sigui desenvolupable cal que contingui rectes superfície reglada i que el vector normal a la superfície sigui constant al llarg de cada recta En són exemples els cons, els cilindres i les superfícies constituïdes per totes les tangents a una corba en l’espai Qualsevol superfície desenvolupable és d’un d’aquests tres tipus citats
equació de Laplace
Física
Matemàtiques
Equació diferencial en derivades parcials expressada per la fórmula Δf = 0, Δ essent el laplacià.
Les funcions que són solució de l’equació de Laplace són anomenades funcions harmòniques , i tenen una especial aplicació en la teoria del potencial En el cas que f sigui una funció de la variable complexa z = x + iy , l’equació de Laplace, que en aquest cas pren la forma ∂ 2 f /∂ x 2 + ∂ 2 f /∂ y 2 = 0, expressa la condició necessària i suficient perquè f sigui derivable
potència
Matemàtiques
Donats un nombre a
, anomenat base
, i un nombre natural n
, anomenat exponent
, producte
a n
de n
factors iguals a a
, és a dir,
.
Hom generalitza la noció de potència al cas en què l’exponent és un enter negatiu, mitjançant la fórmula a -n =1/a n , i al cas en què l’exponent és un nombre racional, mitjançant la fórmula La generalització al cas que l’exponent sigui un nombre real qualsevol té lloc mitjançant la funció exponencial , i en el cas que l’exponent sigui un nombre complex, mitjançant la fórmula de De Moivre Les propietats més importants de les potències són
binomi de Newton
Matemàtiques
Fórmula per a calcular la potència enèsima d’un binomi, anomenada també teorema del binomi.
En el cas que l’exponent n del binomi sigui un nombre natural, la fórmula pot ésser demostrada per inducció, i la seva expressió és on els coeficients n k , anomenats coeficients binomials , són donats per la fórmula Aquesta expressió, que ja utilitzà NTartaglia, fou ampliada per INewton en el cas d’exponents negatius i fraccionaris i per LEuler en el cas d’exponents irracionals En el cas, però, que l’exponent n no sigui un nombre natural, l’anterior expressió esdevé una sèrie infinita i, per tant, només té sentit quan la sèrie és convergent, cosa que imposa certes…
exponent de convergència
Matemàtiques
En una successió (
U n
), el menor dels nombres ε>0 tals que la sèrie
sigui convergent.
relació d’equivalència
Matemàtiques
Relació binària entre els elements d’un conjunt que permet d’establir una classificació d’aquests elements de tal manera que resti cadascun en una classe, dita d’equivalència, i aquestes classes no tinguin cap element comú.
Perquè una relació sigui d’equivalència cal que sigui reflexiva, simètrica i transitiva relació Tota relació d’equivalència estableix una classificació del conjunt i tota classificació determina una relació d’equivalència Són equivalents dos elements que pertanyen a la mateixa classe El conjunt de les classes considerada cadascuna com un nou element és anomenat conjunt quocient del conjunt de partida C per a aquesta relació R , i s’escriu C/R Una aplicació d’un conjunt en un altre determina una relació d’equivalència entre els elements del conjunt original, prenent…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- Pàgina següent
- Última pàgina