Resultats de la cerca
Es mostren 14 resultats
teorema de Menelau
teorema de Menelau
© fototeca.cat
Matemàtiques
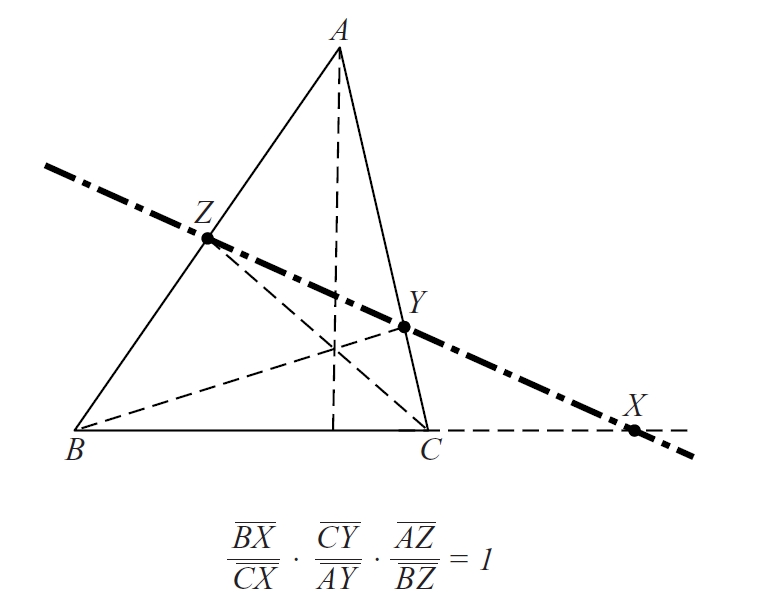
Teorema segons el qual tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB, respectivament, d’un triangle ABC, estan alineats si, i solament si, (BX⁄CX)·(CY⁄AY)·(AZ ⁄ BZ) = 1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui +1 X , A , B Y , B , C Z , C , A = 1 Aquest teorema és dual del teorema de Ceva
teorema de Ceva
teorema de Ceva
Matemàtiques
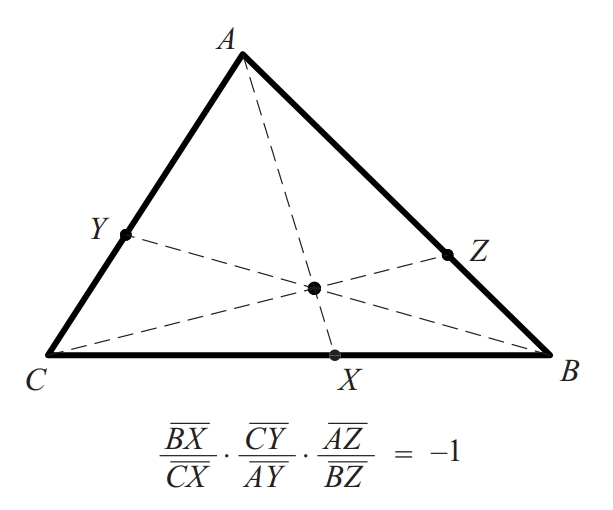
Teorema segons el qual, prenent tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB d’un triangle de vèrtexs A, B i C, les rectes AX, BY i CZ són concurrents si, i solament si, (BX ⁄ CX) · (CY ⁄ AY) · (AZ ⁄ BZ) = –1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui –1 X , A , B Y , B , C Z , C , A = –1 Aquest teorema és dual del teorema de Menelau
Albert Thoralf Skolem
Lògica
Matemàtiques
Lògic i matemàtic noruec.
Treballà especialment en el camp de la resolució de les equacions diofàntiques, en el de l’estudi axiomàtic dels enters naturals i en el de la caracterització dels automorfismes de les àlgebres simples En lògica, contribuí al desenvolupament de la teoria intuïcionista
símplex
Matemàtiques
Conjunt format per n + 1 punts p 0, p 1, ..., Pn linealment independents d’un espai euclidià de dimensió major que n i tots els punts de la forma x =λopo + λ 1p1 + ...
+ λ npn , on λ 0 + λ 1 + + λ n = 1 i 0 ≤λ i , per a cada i Els coeficients λ 0 , λ 1 , , λ n són anomenats coordenades baricèntriques del punt x , el qual pot ésser interpretat com el centre de masses de la distribució determinada en posar pesos λ 0 , λ 1 , , λ n en els punts p 0 , p 1 , , pi Aquest símplex és dit també n-símplex tancat , a fi de distingir-lo del n-símplex obert , en el qual totes les coordenades baricèntriques són estrictament positives Un símplex és degenerat si els punts determinants no són independents Els punts pi són dits vèrtexs i cada collecció de r + 1 vèrtexs…
Johann Bernoulli
Matemàtiques
Matemàtic suís.
Començà estudiant medicina, però es decantà molt aviat per les matemàtiques Fou deixeble del seu germà Jakob, que l’inicià en l’obra de Leibniz, de la qual fou propagador Estigué a París 1690-95, on redactà un curs de càlcul per al marquès de L’Hôpital hom creu que la coneguda regla de L’Hôpital és deguda a Johann Bernoulli El 1691 determinà les tangents i els radis de curvatura de moltes corbes planes i donà el primer exemple de coordenades polars Fou professor a Groningen 1695-1705 i, des de la mort del seu germà Jakob, a Basilea 1705, on fou mestre d’Euler Proposà i resolgué el problema de…
Yves Meyer
Matemàtiques
Matemàtic francès.
Graduat en matemàtiques per l’Escola Normal Superior ENS de París 1957, obtingué el doctorat per la Universitat d’Estrasburg el 1966 Ha desenvolupat la seva trajectòria docent i de recerca successivament a l’escola militar Prytanée 1960-63, la Universitat d’Estrasburg 1963-66, la Universitat de París-Sud 1966-80, l’École Polytechnique 1980-86, la Universitat de París-Dauphiné 1985-95 i al centre de matemàtiques CMLA de l’ENS fins a la jubilació 2008, d’on fou nomenat professor emèrit Ha fet aportacions a la teoria dels nombres i, especialment, a l’anàlisi harmònica, camp en el qual, en…
axiomàtica
Filosofia
Matemàtiques
Conjunt d’axiomes no contradictoris i independents que es formulen per a poder desenvolupar una teoria d’una manera deductiva lògicament correcta.
La matèria que es presta més a ésser tractada en forma axiomàtica és la matemàtica, bé que el mètode és aplicable al desenvolupament teòric d’altres ciències física, economia, estadística, etc Cada una de les proposicions admeses com a base de l’estudi axiomàtic d’una teoria és anomenada axioma o postulat aquests dos mots, en matemàtiques, són considerats sinònims Un sistema de postulats és un conjunt de proposicions breus que tradueixen les veritats fonamentals de la teoria a la qual serveixen de base És desitjable que els postulats d’un sistema siguin simples , és a dir, que…
recta
Matemàtiques
Línia que en l’espai ordinari dóna la distància més curta entre dos punts; la imatge material més simple és la donada per un cordill tibant.
En realitat aquesta imatge correspon millor a un segment o tros de recta la recta és, de fet, infinita en tots dos sentits La geometria no dóna cap definició directa de recta, sinó que, en fixar l’axiomàtica o conjunt de proposicions bàsiques de les quals hom dedueix totes les altres que constitueixen les diverses geometries, resten definits indirectament els conceptes fonamentals punt, recta, pla L’intent de definir cada element a partir d’altres de més simples no pot prosseguir indefinidament sense caure en un cercle viciós, puix que algun element ha d’ésser el primer d’aquesta…
volum
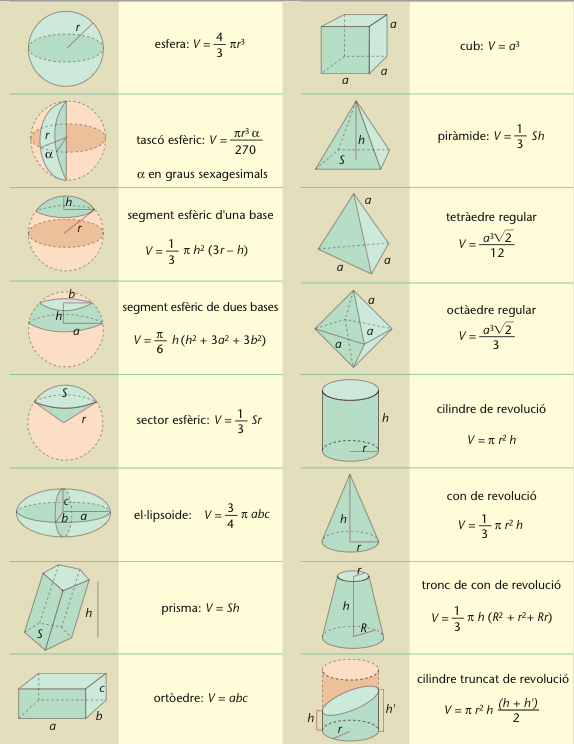
Fórmules per al càlcul de volums
© Fototeca.cat
Matemàtiques
Grandor o mesura de la porció de l’espai ocupada per un cos.
El volum és una mesura que a tota regió de l’espai de tres dimensions assigna un nombre real positiu, de manera que es compleix la propietat additiva, és a dir, que el volum d’un cos és igual a la suma dels volums de qualsevol partició que hom hagi fet en el cos divisió del cos en parts disjuntes Prenent com a base que el volum assignat a un cub de costat a és a 3 , el volum de qualsevol altre cos pot ésser calculat com l’ínfim de la suma dels volums dels cubs disjunts que plegats cobreixen el cos Així, el volum d’una figura plana és zero El volum dels cossos geomètrics simples…
Gottfried Wilhelm Leibniz
Filosofia
Física
Història
Matemàtiques
Història del dret
Filòsof alemany de cultura enciclopèdica, com ho testifiquen les seves aportacions en altres terrenys: matemàtica, física, història, dret i religió.
Conseller de l’elector de Magúncia 1672, fou enviat a París, on residí quatre anys, decisius per a la seva formació Sis anys abans, però, quan aspirava a una plaça de professor de filosofia a Leipzig, ja publicà una Dissertatio de arte combinatoria , inspirada en l' Ars magna de Llull Bibliotecari i historiògraf dels ducs de Hannover, viatjà per tot Alemanya i Itàlia intensificà, així, els seus contactes amb molts savis de l’època També es relacionà amb el cercle lullià de Magúncia i fou amic de Buchels, collaborador de Salzinger en l’edició maguntina de les obres de Llull 1721-42 Entre les…