Resultats de la cerca
Es mostren 79 resultats
distribució
t
n
Matemàtiques
Siguin Y
i Z
variables aleatòries independents tals que Y
sigui N
(0,1) i Z
tingui una distribució x 2
amb n
graus de llibertat i hom consideri la variable aleatòria
Aquesta variable té la funció de distribució i densitat La funció de distribució S n x rep el nom de distribució t amb n graus de llibertat o de distribució Student amb n graus de llibertat en memòria de l’estadístic anglès WS Gosset, que escrigué amb el pseudònim de Student
funció d’autocorrelació
Matemàtiques
Donada una funció f(t), funció definida per F(τ)=(1/2T)∫ T - T f(t)f(t-τ) dt
.
Si f t és una magnitud variable en el temps, F τ dóna una idea de la mesura en què els valors futurs de f t poden ésser prevists a partir dels seus valors passats
uniformitat
Matemàtiques
Família F de subconjunts d’un producte cartesià T × T
.
Compleix x,x pertany a qualsevol element de F , per a tot x si V és de F, V - 1 = { x,y | y,x és de V} és també de F i per a tot V de F existeix un altre W tal que WW = { x,z | existeix y en T i x,y ∈ W , y,z ∈ W} és un subconjunt de V Tota uniformitat dóna lloc a un espai topològic i aquest és metritzable la seva topologia prové d’una distància si és de Hausdorff i la uniformitat té una base numerable Per exemple, si T és un espai mètric, amb distància d , el conjunt de subconjunts de T × T , U ∈ = { x,y | d x,y πε} és una uniformitat La parella T,F , on T és conjunt i F…
vector tangent
Matemàtiques
Donada una corba qualsevol x=x(t), y= y(t), z=z(t), i un punt [x(t0), y(t0), z(t0)], vector paral·lel a [x’(t0), y’(t0), z’(t0)] i de mòdul unitat.
La recta que, passant pel punt x t 0 , y t 0 , z t 0 té per vector director el vector tangent, és anomenada recta tangent a la corba , amb la qual cosa hom generalitza la noció de recta tangent a una corba plana per al cas de les corbes guerxes
funció periòdica
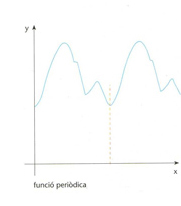
Funció periòdica
© Fototeca.cat
Matemàtiques
Funció f
: D
⊂ℝ→ℝtal que existeix un nombre T
∈ℝ-{0} que satisfà que, per a tot x
∈ D, x
+ T∈ D
i f
( x
+ T
)= f
( x
).
Hom diu aleshores que T és un període de la funció f bé que hom anomena, pròpiament, període al més petit nombre T que satisfà les condicions esmentades En són exemples les funcions trigonomètriques sinus i cosinus que tenen un període 2π
punt de retrocés
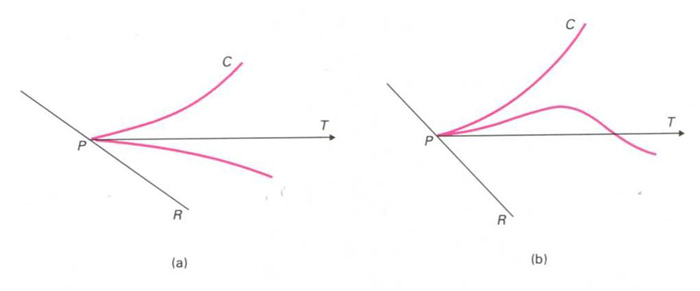
Punt de retrocés de primera (a) i de segona (b) espècie
© fototeca.cat
Matemàtiques
Donada una corba plana C
, punt P
d’aquesta corba en el qual existeix una tangent T
de tal manera que existeix un entorn U
de P
i una recta R
, diferent de T
, tals que els punts de C ∩U
pertanyen al mateix semiplà respecte a R
.
És un punt de retrocés de primera espècie si existeix un entorn U´ de P tal que els punts de C ∩U´ són repartits entre els dos costats de T , i és un punt de retrocés de segona espècie si són al mateix costat respecte a T Un punt de retrocés és anomenat també cúspide o punt cuspidal
element absorbent
Matemàtiques
Element z pertanyent a un conjunt E tal que per a tot x compleix zTx = xTz = z, essent T una determinada llei de composició.
Un element absorbent és anomenat també un zero respecte de T
equacions d’Einstein-Lorentz
Matemàtiques
Si hom considera dos observadors que es mouen amb velocitat relativa v en la direcció d’un eix comú que hom pren com a eix de les ics, la posició i el temps en què s’esdevé un succés P seran amidats per un observador en funció de les coordenades x, y, z i del temps t i, per l’altre, en funció d'x', y', z' i t', dependents del seu sistema referencial.
Les equacions d’Einstein-Lorentz estableixen el lligam que hi ha entre aquestes dues quaternes de nombres i són que admeten la transformació inversa que hom obté canviant x , y , z , t per x ', y' , z' , t' i canviant el signe de v És d’interès observar que 1/ c = 0 proporciona la transformació clàssica o galileana Dit altrament, si v és força negligible davant de la velocitat c de la llum, aleshores la transformació d’Einstein-Lorentz esdevé la transformació de la mecànica clàssica Cal remarcar, finalment, que les transformacions d’…
semblança
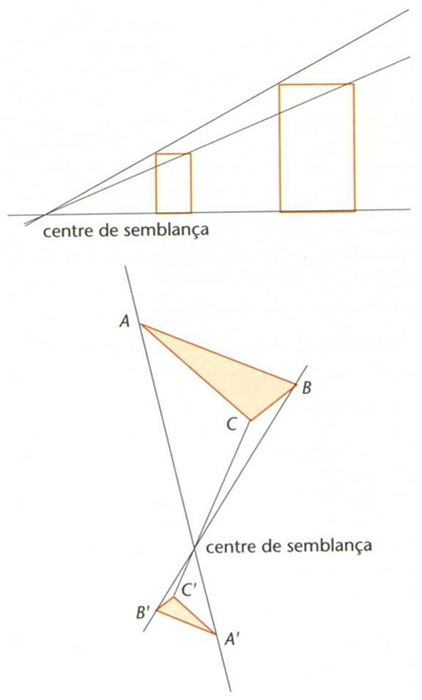
Dues semblances directes
© Fototeca.cat
Matemàtiques
Transformació geomètrica T de ℝn en ℝn tal que la distància entre les imatges de dos punts qualssevol és igual a la distància entre aquests dos punts multiplicada per una quantitat constant positiva dita raó de la semblança.
És a dir, d T x, T y = k, d x, y Dues figures són anomenades semblants si hi ha una semblança que transforma l’una en l’altra Les semblances conserven la forma de les figures però en canvien la grandària, eixamplant-la o reduint-la segons que la raó sigui respectivament major o menor que 1 Les semblances de raó 1 són dites isometries o moviments rígids , els quals són sempre el resultat de compondre una translació amb una transformació lineal ortogonal que conserva els angles Les homotècies són exemples típics de semblances Tota semblança és el resultat d’aplicar…
transformació simètrica
Matemàtiques
Transformació T d’un espai euclidià E tal que Tx·y = x·Ty si · indica el producte escalar de E.
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- Pàgina següent
- Última pàgina