Resultats de la cerca
Es mostren 8 resultats
translació
Matemàtiques
Transformació geomètrica que a cada punt M
del pla n’hi associa un altre M’
de manera que el vector de manera que el vector
sigui un representant d’un vector lliure
prefixat, anomenat vector de la translació
Les translacions són isometries que en el pla conserven el sentit de les rotacions i en l’espai el caràcter dels tríedres, no tenen punts dobles i en les quals les rectes i els plans parallels al vector de translació són invariants El conjunt de totes les translacions del pla o de l’espai formen un grup commutatiu amb l’operació composició, el qual és isomorf al grup additiu dels vectors lliures ordinaris associats al pla o a l’espai considerat Si és el vector característic d’una translació, el punt transformat d’un punt M x 1 ,x 2 ,x 3 és el punt M' x' 1 ,x' 2 ,x'…
equipol·lència
Matemàtiques
Relació d’equivalència entre vectors fixos de l’espai euclidià.
Dos vectors són equipollents si existeix una translació que transforma l’un en l’altre Les classes de vectors equipollents són anomenades vectors lliures vector
teorema de Bonnet
Matemàtiques
Teorema segons el qual els coeficients de les formes fonamentals d’una superfície determinen localment la parametrització de la superfície, llevat de composició amb transformacions ortogonals pròpies i translacions.
Concretament, si E , F , G , e , f , g són funcions diferenciables definides en un obert V ⊂ ℝ 2 , amb E > 0, G > 0 i EG – F 2 > 0 tals que satisfan les equacions de compatibilitat de Gauss i de Mainardi-Codazzi, aleshores per a cada q ∈ V existeix un entorn U ⊂ V de q i un difeomorfisme x U → x U ⊂ ℝ 3 tal que la superfície regular x U ⊂ ℝ 3 té E , F , G , e , f , g per coeficients en les seves formes fonamentals Amés, si U és connex i x’ U → x’ U ⊂ ℝ 3 és un altre difeomorfisme que satisfà les mateixes condicions, aleshores existeix una translació T i una…
semblança
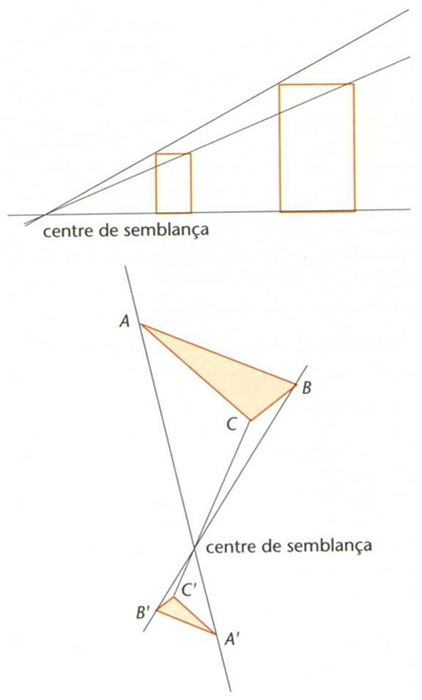
Dues semblances directes
© Fototeca.cat
Matemàtiques
Transformació geomètrica T de ℝn en ℝn tal que la distància entre les imatges de dos punts qualssevol és igual a la distància entre aquests dos punts multiplicada per una quantitat constant positiva dita raó de la semblança.
És a dir, d T x, T y = k, d x, y Dues figures són anomenades semblants si hi ha una semblança que transforma l’una en l’altra Les semblances conserven la forma de les figures però en canvien la grandària, eixamplant-la o reduint-la segons que la raó sigui respectivament major o menor que 1 Les semblances de raó 1 són dites isometries o moviments rígids , els quals són sempre el resultat de compondre una translació amb una transformació lineal ortogonal que conserva els angles Les homotècies són exemples típics de semblances Tota semblança és el resultat d’aplicar successivament…
acció d’un grup en un conjunt
Matemàtiques
Donat un grup G i un conjunt X, acció d’assignar a cada element g de G una aplicació bijectiva σg de X en X de tal manera que σe (e és l’element neutre de G) és la identitat de X i que σg’ o σg = σg’g, qualssevol que siguin els elements g i g’ de G.
Si g és un element de G , la inversa de l’aplicació σ g és σ g–1 Per exemple, si X , V és un espai afí, l’aplicació v → t v que assigna a cada vector v de V la translació t v definida per v és a dir, t v x = x + v per a tot punt x de X és una acció del grup additiu V ,+ en X Un altre exemple és l’acció per conjugació del grup G de matrius reals invertibles d’ordre n en el conjunt X de matrius reals d’ordre n , definida per la relació σ g x = gxg -1 Si X és un conjunt amb estructura per exemple un espai vectorial i les aplicacions σ g són automorfismes d’aquesta…
moviment
Matemàtiques
Aplicació d’un espai mètric en ell mateix que conserva la distància.
Actualment hom tendeix a anomenar-lo isometria El conjunt de moviments definits sobre un espai, amb l’operació de composició o producte de moviments, constitueix un grup En particular, és interessant l’estudi dels moviments al pla i a l’espai ordinaris El grup dels moviments del pla és generat per les simetries axials, és a dir, tot moviment del pla pot ésser descompost en producte d’un cert nombre de simetries axials Els de nombre parell són anomenats moviments directes , conserven el sentit del pla i són un subgrup del grup de moviments els altres són anomenats moviments inversos Dins el…
vector
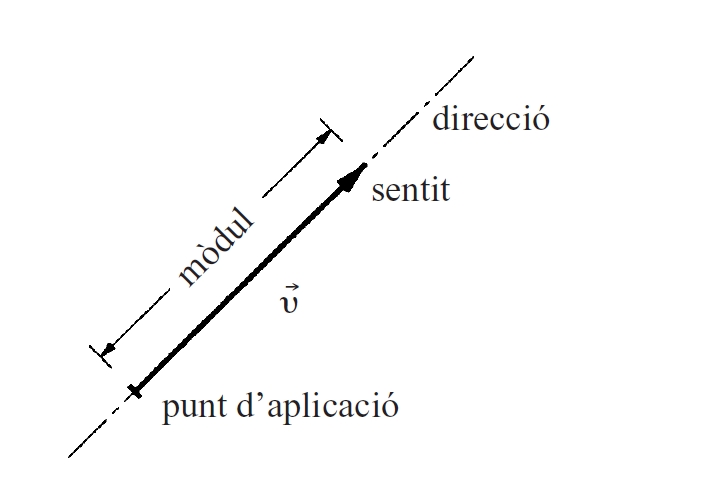
Vector
Física
Matemàtiques
Element d’un espai vectorial.
Des del punt de vista geomètric, a tot vector se li pot associar direcció, mòdul i sentit, i un punt d’aplicació Segons les seves posicions relatives, es parla de vectors simètrics, oposats, conjugats, ortogonals, etc Fixada una base de vectors e 1 ,, e n en un espai vectorial E de dimensió n base d’un espai vectorial, tot vector x de E pot ésser expressat en forma única com a combinació lineal dels elements de la base x = x 1 e 1 + + x n e n Així, x resta determinat pels nombres x 1 , x 2 ,, x n , els quals són dits components de x hom ho escriu x = x 1 ,, x n Si en E hom defineix un…
sanefa

Els set tipus de sanefes
Matemàtiques
Figura plana en la qual tots els moviments rígids que pertanyen al seu grup de simetria deixen una recta invariant i totes les translacions que hi pertanyen són múltiples d’una translació donada no nul·la, que marca el ritme de repetició de la figura. Hi ha set formes de generar sanefes en el pla.