Resultats de la cerca
Es mostren 5503 resultats
Ginebra
La catedral de Ginebra
© B. Llebaria
Ciutat
Capital del cantó de Ginebra, Suïssa, a l’extrem sud-oest del llac Léman, o de Ginebra.
El Roine surt pel sud del llac i divideix la ciutat en dues parts A l’esquerra s’alça el turó on hi ha el nucli antic de la ciutat, amb la catedral al punt més alt és el centre administratiu, amb carrers estrets i tortuosos Rue de la Cité, Grand Rue Al S i el SW l’expansió urbana es produí cap a l’Arve i al punt d’aiguabarreig amb el Roine, al NW amb els barris del Petit Saconnex, el Grand Pré i La Servette, al N i el NE cap al Montbrillant i Le Sacheron, i a l’E i el SE amb el barri d’Eaux-Vives Ginebra ha conservat una funció administrativa de caràcter supranacional és seu de diversos…
contrapunt
Exemple 1 a i b
© Fototeca.cat/ Jesús Alises
Música
Combinació de línies musicals simultànies en un tot orgànic.
El fenomen contrapuntístic es basa en la capacitat de l’oïda per a percebre, de manera distinta, diferents fenòmens musicals combinats sense perdre de vista la combinació mateixa Així, l’oïda distingeix la melodia i l’acompanyament d’una cançó, o les dues veus que formen un cànon, sense deixar de sentir-ne la suma, és a dir, la cançó o el cànon La capacitat de combinar de manera simultània diferents elements en un tot orgànic és un dels trets més distintius de la música, que segurament no té un equivalent en les altres arts Exemple 1 c i d © Fototecacat/ Jesús Alises D’altra banda, es…
independència estocàstica
Matemàtiques
Relació entre dos esdeveniments A i B d’un espai de probabilitat en la qual es compleix que la possibilitat que es donin A i B alhora és igual al producte de les probabilitats que es donin A i B independentment, és a dir, P(A ∩B) = P(A) · P(B)
.
Quan això es compleix, els esdeveniments A i B són anomenats independents
funció còncava
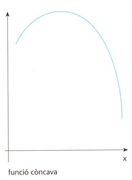
Funció concàva
© Fototeca.cat
Matemàtiques
Funció f:(a,b)⊂ℝ→ℝtal que per a tot α∈(0,1) se satisfà f(αx+(1—α)y)≥αf(x)+(1—α)f(y), on a<x<b i a<y<b.
El significat geomètric és que per a tot interval x,y ⊂ a,b la corda que uneix f x amb f y és situada per sota de l’arc que uneix f x amb f y
variació d’una funció
Matemàtiques
Donat un interval [a, b], suprem, per a totes les possibles particions de [a, b], de la suma de les oscil·lacions de la funció en tots els subintervals de la partició.
És a dir, si a = x o < x 1 < < x n - 1 < x n = b és una particiò P qualsevol de a, b i | f x i + 1 - f x i | l’oscillació de la funció en un subinterval arbitrari x i , x i + 1 i essent aleshores la variació de f en a, b serà V f = sup { P , P∈ℱ} , on ℱdesigna el conjunt de totes les particions de l’interval a, b Si V f és un nombre finit, hom diu que la funció f té variació fitada en l’interval a, b Tota funció real definida en un interval tancat que s’expressi com a diferència de dues funcions…
enter
Matemàtiques
Classe d’equivalència que la relació (a,b)R(c,d), si, i només si, a+d = b+c, indueix en el conjunt producte ℕ × ℕ (ℕ essent el conjunt dels nombres naturals).
El conjunt d’aquestes classes d’equivalència conjunt quocient és el conjunt dels nombres enters ℤ = {0, ±1, ±2, ±3, } Hom anomena representant canònic d’un enter a,b aquell en què o a o b és 0 Si l’esmentat representant canònic és de la forma m, 0, aquest és un enter positiu , representat també per + m si és la forma 0, m , es tracta d’un enter negatiu , habitualment representat per - m i si és 0,0, és l' enter nul , o sigui 0 En el conjunt ℤ hom defineix dues operacions la suma és definida per a, b + c, d = a + c , b + d , i el…
aplatament
Geologia
Relació de la diferència del radi equatorial o semieix major ( a
) i el radi polar o semieix menor ( b
), al radi equatorial a: A = (a-b
)/ a
.
Al congrés de geodèsia celebrat a Madrid l’any 1924 fou adoptat com a ellipsoide internacional el de Hayford, amb els següents valors semieix major a 6378388 m semieix menor b 6356909 m, de què resulta un aplatament de A = a-b / a = 1/297 Modernament, la Terra no és considerada un ellipsoide rígid, sinó elàstic, en forma de pera, que ha rebut el nom de geoide
funció convexa
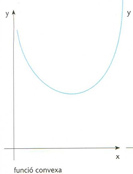
Funció convexa
© Fototeca.cat
Matemàtiques
Funció f:(a,b)⊂ℝ→ℝtal que per a tot α∈(0,1) se satisfà f(αx+(1-α)y)≤αf(x)+1-α)f(y), on a<x<b i a<y<b.
El significat geomètric és que per a tot interval x,y ⊂ a,b la corda que uneix f x amb f y és situada per sobre de l’arc que uneix f x amb f y
teorema de Rolle
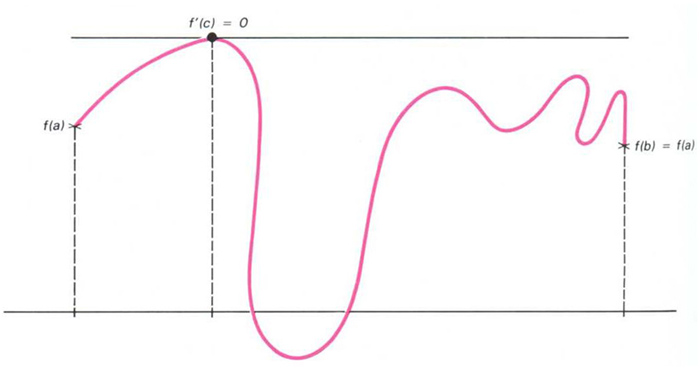
Teorema de Rolle
© fototeca.cat
Matemàtiques
Teorema segons el qual si f és una funció contínua en tots els punts d’un interval tancat [a,b] i té derivada en cada punt de l’interval obert (a,b), aleshores si f (a) = f (b), existeix un punt c en (a,b) tal, que f´ (c) = 0.
És a dir, existeix una tangent horitzontal a la corba representativa de la funció en un punt c , entremig de a i b
trencat
Matemàtiques
Nombre que denota un agregat de parts alíquotes d’una unitat, per mitjà de dos enters a i b, que hom escriu a/b
.
El nombre a és el numerador , i b , el denominador És conegut també com a nombre fraccionari fracció, nombre racional