Resultats de la cerca
Es mostren 964 resultats
el·líptic | el·líptica
angle en el centre
Matemàtiques
Angle que té el vèrtex al centre d’una circumferència i els costats del qual són dos radis.
Val igual que l’arc que subtendeix
el·lipsoide
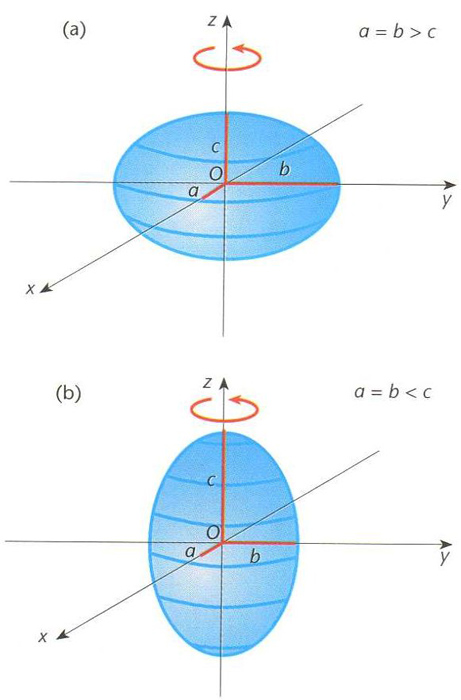
El·lipsoide aplatat (a) i allargat (b) obtinguts per rotació d’una el·lipse, prenent com a eix de la rotació el que conté, en el primer cas, el semieix menor d’aquesta el·lipse i, en el segon, el semieix major
© Fototeca.cat
Matemàtiques
Superfície de segon grau o quàdrica amb centre l’equació de la qual és (
x 2
/a 2
)+(
y 2
/b 2
)+(
z 2
/c 2
)=1 si els eixos de coordenades són els propis de la quàdrica.
Una ellipse que giri al voltant del seu eix menor determina un ellipsoide aplatat , anomenat també esferoide oblat i una ellipse que giri al voltant del seu eix major determina un ellipsoide allargat , anomenat també esferoide prolat Quan a=b=c=r l’ellipsoide esdevé una esfera de radi r
el·lipse
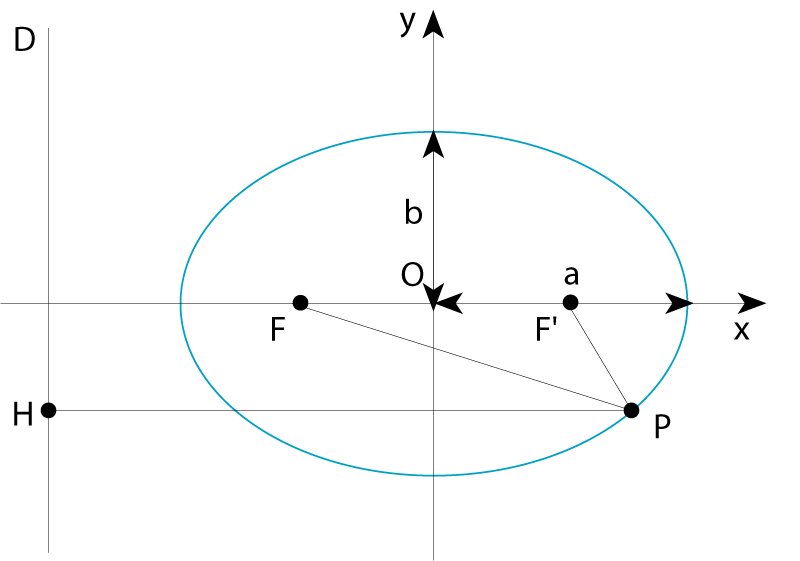
El·lipse de semieixos a i b; D és la directriu associada al focus F
© Fototeca.cat
Matemàtiques
Corba tancada que resulta de la intersecció d’una superfície cònica amb un pla que no és paral·lel a cap generatriu ni a l’eix d’aquella; és doncs, una cònica
.
La seva equació en coordenades cartesianes referides als seus dos eixos perpendiculars de simetria és x 2 / a 2 + y 2 / b 2 =1, a essent el semieix major i b el semieix menor L’ellipse és el lloc geomètric dels punts P del pla tals que la suma de llurs distàncies a dos punts fixos F i F ´, anomenats focus , és una quantitat constant, independent del punt P concret, igual al doble del semieix major, PF + PF ´=2 a és també el lloc geomètric dels punts P tals queel quocient de llurs distàncies a un…
paraboloide el·líptic
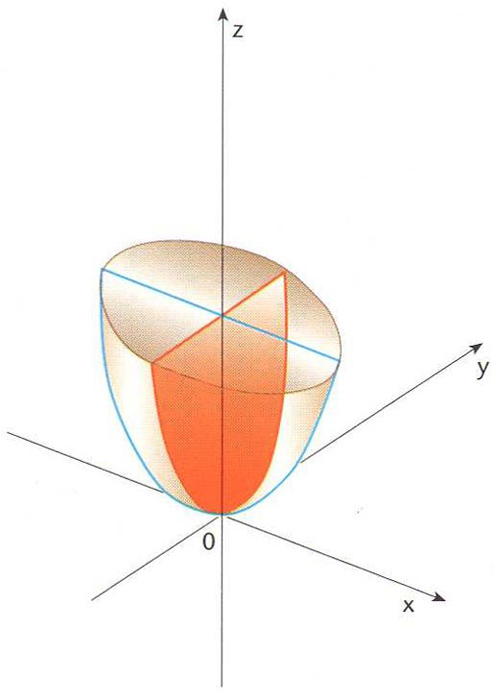
Paraboloide el·líptic on hi ha traçada una el·lipse i una paràbola
© Fototeca.cat
Matemàtiques
Paraboloide d’equació
x 2
/a 2
+
y 2
/b 2
= 2 z
, on a
i b
són constants.
La seva intersecció amb un pla que contingui l’eix de simetria és una paràbola, mentre que la intersecció amb un pla perpendicular a l’anterior dóna una ellipse
integral el·líptica
Matemàtiques
Integral de tipus ∫ Rdz
on φ(z) és un polinomi en z de grau 3 o 4 i amb coeficients complexos, i on R
(i, w) és una funció racional de variables independents z,w.
Aquest nom prové del fet que, en intentar rectificar un arc d’ellipse és a dir, en intentar calcular la longitud d’un arc d’ellipse, sorgeix una integral d’aquesta mena Tota integral ellíptica pot ésser transformada per canvis adequats de variables com una suma d’integrals elíptiques elementals Les integrals ellíptiques elementals són de tres tipus integral ellíptica de primer tipus integral ellíptica de segon tipus integral ellíptica de tercer tipus Quan una integral ellíptica s’ha descompost en suma d’integrals ellíptiques elementas es troba en forma estàndard de Legendre-Jacobi
funcions el·líptiques de Jacobi
Matemàtiques
Donats dos reals no nuls, a i a´, tals que a2 + a´2 = 1, funcions inverses de les funcions .
Les funcions inverses de f, g i h es denoten, respectivament, per sn, cn i dn i satisfan les següents propietats cn u + sn snu cnu = 1 dn 2 u + a 2 sn 2 u = 1 cn´ u = -sn u dn u dn'u = - a 2 sn u cn u
Pitàgores
Filosofia
Matemàtiques
Filòsof i matemàtic grec, fundador de l’escola o secta politicoreligiosa que porta el seu nom.
Malgrat la incertesa de les notícies que hom en té, sembla que s’establí, procedent de l’Àsia Menor, a Crotona ~530 aC, on fundà una comunitat ascètica centrada en l’estudi de les matemàtiques i activa en els afers polítics de la ciutat, i d’on, ja vell, hagué de fugir a la veïna Metapont arran d’una rebellió que hi tingué lloc La saviesa del mestre no fou divulgada pels seus deixebles, tal com establien els preceptes de la comunitat, motiu pel qual és difícil de destriar la part de les creences del pitagorisme que correspon a Pitàgores mateix i no a aportacions dels seus …
Elements
Matemàtiques
Tractat de matemàtiques atribuït a Euclides i que ha estat, fins a mitjan segle XIX, l’autoritat màxima dins el camp de les matemàtiques generals.
Sintetitzà perfectament el treball dels antics matemàtics grecs i li donà una major coherència lògica amb les noves definicions de línia i de pla i, sobretot, amb la introducció del cinquè postulat millorà també l’ordenació i les demostracions de les proposicions Malgrat ésser un text de compilació, hom no pot posar en dubte que la planificació global de l’obra i el mètode expositiu, com també un bon nombre dels seus teoremes, són obra del mateix Euclides
Arquimedes
Física
Matemàtiques
Matemàtic i físic grec.
Fill d’un astrònom, hom el suposa parent del tirà de Siracusa, Hieró Fou mort per un soldat romà quan les tropes de Marcel saquejaren Siracusa en el curs de la segona guerra Púnica És difícil de destriar la veritat de la llegenda en els altres detalls de la seva biografia Es destacà en geometria pura Havia estudiat Euclides i tingué alguna relació amb Eratòstenes Hom li pot suposar, però, una certa oposició enfront de la ciència oficial de l’època detinguda pels professors que residien a Alexandria, atesos la profunda originalitat de la seva obra científica, el dialecte dòric en què fou…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina