Resultats de la cerca
Es mostren 108 resultats
suma
Matemàtiques
Resultat d’una addició
.
És a dir que, donats dos objectes, la suma és un altre objecte determinat a partir d’aquests per addició La suma aritmètica entre nombres com ara 4+2 = 6 a + b = c equival a dir que la reunió de dos conjunts que tenen a i b elements, respectivament, és un conjunt que té a + b elements + és el símbol que indica suma En l’expressió a + b , la quantitat a és anomenada augend i b, addend tant a com b són anomenats sumands La suma de trencats racionals o fraccionaris és definida per la regla La suma d’irracionals ha d’ésser indicada després de fer les simplificacions possibles per exemple, Hom…
sèrie
Matemàtiques
Suma indicada d’un conjunt finit o infinit ordenat de termes.
La teoria de sèries s’ocupa especialment del cas infinit numerable Així, una sèrie és donada per una successió de nombres a₁ , a₂ , , a n , on a n és dit terme general n -èsim de la successió i una successió associada formada per les sumes parcials a₁ , a₁ + a₂ , a₁ + a₂ + a₃ , , a₁ + + a n , Simbòlicament hom representa una sèrie per , o bé a₁ + a₂ + a n + Si la successió de sumes parcials és convergent cap a un límit S , hom diu que la sèrie és convergent i de suma S En cas de no existir aquest límit, la sèrie és dita divergent Una sèrie és dita positiva o negativa segons que tots…
teorema d’Apol·loni
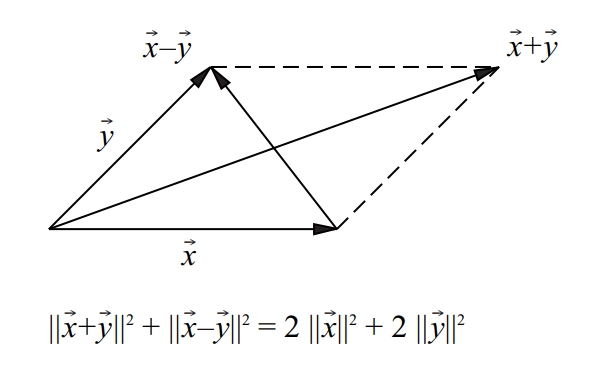
Formulació vectorial del teorema d’Apol·loni
Matemàtiques
Teorema de geomètria mètrica segons el qual en tot triangle la suma dels quadrats de dos costats és igual al doble de la suma del quadrat de la meitat del tercer costat més el quadrat de la mitjana corresponent a aquest darrer costat.
En la seva formulació actual, amb vectors i normes, aquest teorema s’anomena també llei del parallelogram i estableix que la suma dels quadrats de les dues diagonals del parallelogram és igual a la suma dels quadrats dels quatre costats
determinant
Matemàtiques
Donada una matriu quadrada d’ordre
n, A=(a i j
)
, suma dels n
! termes
.
Aquestes termes corresponen a les diferents maneres de fer el producte de n elements de A de manera que n'hi hagui un, i només un, de cada fila i de cada columna Els n termes s’obtenen en fer totes les permutacions dels n subíndexs de columna 1,n mantenint fixos els índexs de fila el nombre r del terme és la signatura de la permutació k 1 k n El determinant de A acostuma a ésser representat tancant la matriu amb dues barres verticals El nombre n és l' ordre del determinant Un determinant pot ésser representat en termes dels elements i cofactors cofactor de qualsevol fila o columna de la…
addició
Matemàtiques
Operació consistent a fer correspondre a cada parell d’elements d’un determinat conjunt un altre element del mateix conjunt, anomenat suma.
La definició específica d’addició varia segons els elements als quals hom la vulgui aplicar Entre nombres naturals, el resultat de l’addició, és a dir, la suma, és el nombre natural que representa el conjunt que és reunió de dos conjunts sense elements comuns que representin els addends Si A té dos elements, A = {a,b}, i B té tres elements, B = {c,d,e}, la reunió A∪B = {a,b,c,d,e} té cinc elements, 2 + 3 = 5 Entre nombres reals, el resultat de l’addició és obtingut sumant o restant els valors absoluts dels addends segons que aquests siguin del mateix signe o de signe contrari El signe de la…
problema de Waring
Matemàtiques
Problema de la teoria de nombres proposat pel matemàtic anglès Edward Waring (Old Heath 1734-98) l’any 1770, consistent a demostrar que per a qualsevol nombre natural n existeix un nombre associat K (n), de manera que qualsevol natural pot ésser representat com una suma, com a màxim, de K (n) termes, cada terme essent una potencia n-èsima d’un natural.
En particular, cada nombre natural hauria de poder ésser representat com a suma de quatre quadrats com a màxim i com a suma de nou cubs Aquest problema fou resolt per Hilbert el 1909
polinomi
Matemàtiques
Suma formal de productes de nombres, anomenats coeficients (reals, complexos o, més generalment, elements de qualsevol anell) per elements anomenats variables (generalment denotats per x, y, z, etc), als quals hom atribueix només les propietats algèbriques més simples.
Usant aquestes propietats hom defineix la suma i el producte de polinomis, de manera que els polinomis de n variables formen una àlgebra Substituint les variables per nombres hom obté una funció anomenada funció polinòmica
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina