Resultats de la cerca
Es mostren 19 resultats
àlef
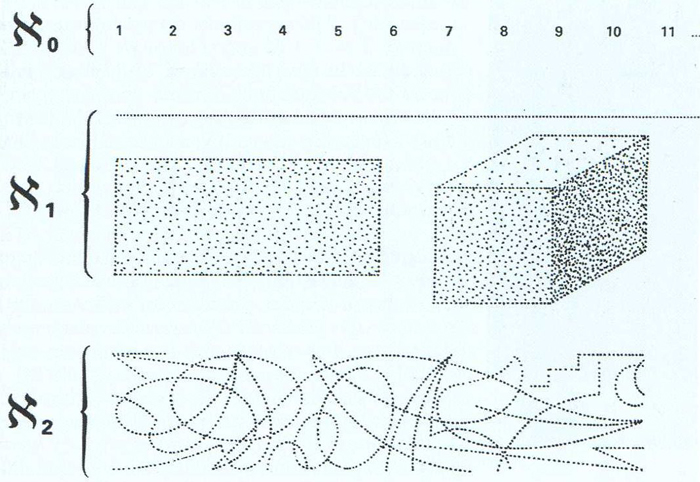
Comparació del cardinal dels naturals, ℵ0, amb els cardinals estrictament més grans: ℵ1, cardinal del continu, i ℵ2, cardinal de les corbes del pla
© Fototeca.cat
Escriptura i paleografia
Matemàtiques
Símbol ℵ que designa el cardinal dels conjunts infinits ben ordenats.
Acompanyat pel subíndex zero indica la classe dels conjunts infinits numerables, que permeten d’establir una correspondència biunívoca amb els nombres naturals, 1, 2, 3, Per exemple, el conjunt dels nombres parells té cardinal, ja que a cada nombre parell 2n hom pot fer correspondre la seva meitat n
punt de fuga
Art
En les representacions perspectives, punt de convergència, en la línia anomenada de l’horitzó, de les rectes o sistemes de rectes paral·leles horitzontals que incideixen en el quadre o pla de projecció.
Les orientacions d’aquesta incidència poden ésser infinites, i infinits poden ésser, per tant, els punts de fuga
supersimetria
Física
Simetria que s’aplica a les partícules elementals per tal de canviar un bosó en un fermió i viceversa.
A les teories que incorporen aquesta simetria, anomenades teories supersimètriques, a cada bosó li correspon un fermió i a cada fermió un bosó L’ús de la supersimetria minimitza els problemes relacionats amb els infinits que apareixen en el càlcul de pertorbacions de les teories de quàntica de camps
renormalització
Física
Tècnica de càlcul emprada en teoria quàntica de camps i en mecànica estadística.
Consisteix, essencialment, a substituir els valors teòrics o arbitraris d’algunes constants físiques com la massa o la càrrega elèctrica, que poden esdevenir infinites en el decurs d’un càlcul, pels valors realment observables La redefinició d’aquestes constants és realitzada mitjançant l’anomenat grup de renormalització , el qual elimina els infinits, sense significat físic, dels càlculs
cercle de quintes

Cercle de quintes
© Fototeca.cat/ Studi Ferrer
Música
Disposició en forma de circumferència de la sèrie de quintes utilitzada per a representar els sistemes d’afinació temprada en els quals tots o una part dels intervals de 5a J són una mica més curts del compte per tal de compensar la coma pitagòrica (coma1) o petita diferència d’afinació que hi ha entre les notes enharmòniques, per exemple do i si♯, fa♯ i sol ♭, etc.
L’eliminació d’aquestes diferències d’afinació entre les notes enharmòniques, que en el cercle de quintes es representa fent-les coincidir en el mateix punt, redueix els teòricament infinits elements de la sèrie de quintes als dotze de l’escala temprada, operació imprescindible per a dur a terme l’afinació dels instruments de teclat La disposició de la sèrie de quintes en forma d’espiral s’utilitza per a representar els sistemes d’afinació justa basats en les quintes pures L’espiral permet expressar la manca de coincidència entre les notes enharmòniques i, per tant, la infinitud…
fitat | fitada
Matemàtiques
Dit dels subconjunts, les successions, les funcions, etc que no prenen valors infinits.
Un subconjunt B d’un conjunt ordenat A ,≤ s’anomena fitat inferiorment en A si existeix algun element k ∈ A dit fita inferior de B tal que k ≤ x per a tot x ∈ B Anàlogament, si existeix un element k´∈A tal que x ≤k´ per tot x∈B , hom diu que B està fitat superiorment en A i que k´ és una fita superior de B Un subconjunt s’anomena fitat si ho està inferiorment i superiorment Aquest concepte s’estén de manera natural a successions i funcions, sempre en el context dels conjunts ordenats i es manté la terminologia emprada Així, una successió s’anomena fitada si el conjunt dels seus termes és…
vaguetat
Lògica
Característica de certes frases o enunciats del llenguatge com ara ‘‘aquest home és calb’’ que donen lloc a proposicions inverificables (això és, que no són clarament i exclusivament veritables o falses) i que incompleixen lleis com ara la transitivitat (perquè no hi ha límít precís entre, en l’exemple citat, un ‘‘calb’’ i un ‘‘no calb’’).
En lògica el problema del tractament formal dels predicats vagues ‘calb’, ‘roig’, ‘gran’, etc s’enfronta a l’aparició de paradoxes com la que resulta d’aplicar-hi un sorites per exemple ‘un home amb un cabell és calb doncs un que en tingui 2,3,,10 000, és calb’, fenomen ja analitzat pels grecs D’ençà de l’aparició de la lògica formal moderna, la posició dels lògics ha estat generalment la de considerar la vaguetat com una característica exclusiva sovint com un “defecte” del llenguatge, inabordable i irrellevant per a la lògica matemàtica clàssica Russell 1923 Entre aquells que…
políedre
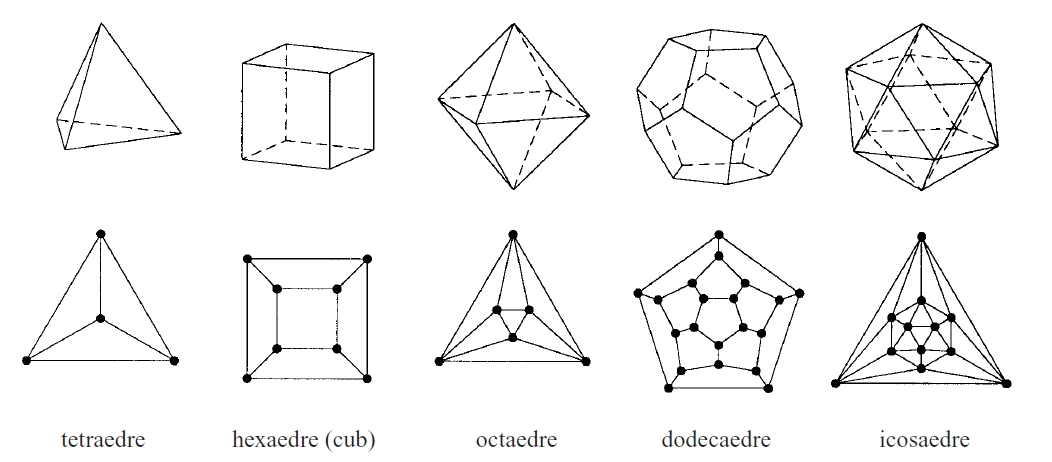
Els cinc políedres regulars i els diagrames de Schlegel associats
© Fototeca.cat
Matemàtiques
Sòlid limitat per quatre o més polígons anomenats cares.
Les interseccions de les cares constitueixen les arestes , i les interseccions de les arestes, els vèrtexs Un políedre és convex si qualsevol secció plana del políedre és un polígon convex Un políedre és còncau si no és convex Un políedre és simple si és topològicament equivalent a una esfera, és a dir, si no té forats Un políedre és regular si té les cares iguals i els angles iguals, essent les cares polígons regulars Des de la Grècia antiga hom sap que existeixen solament cinc políedres regulars el tetràedre regular , l’ hexàedre regular o cub, l’ octàedre regular , el dodecàedre regular i…
discontinuïtat
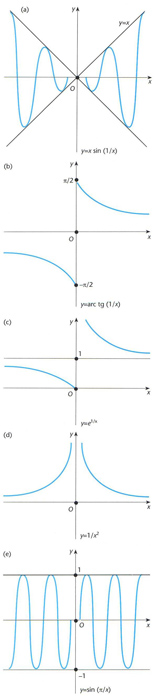
Discontinuïtat d’una funció: (a) discontinuitat evitable en x = 0, amb valor veritable y(0) = 0; (b) discontinuïtat de primera espècie infinita en x = 0, amb salt -2; (c) discontinuïtat de primera espècie infinita amb un punt d’infinit en x = 0; i (e) discontinuïtat de segona espècie finita en x = 0, per inexistència d’ambdós límits laterals quan x 0
© Fototeca.cat
Matemàtiques
Manca de continuïtat d’una funció en un punt o en un conjunt de punts, els quals són anomenats, per extensió, les discontinuïtats de la funció.
Atès que una funció f x és contínua en un punt a si i només si existeix i és igual a f a , la funció f x és discontínua en a si i només si no se satisfà alguna d’aquestes dues condicions, la qual cosa s’esdevé en els següents casos En primer lloc, pot passar que existeixi però que f a no existeixi f no sigui definida a a , o bé que aleshores, a és una discontinuïtat evitable , i la discontinuïtat és evitada redefinint el valor de f x al punt a tot assignant-li el valor el qual és anomenat valor veritable de f x en a En segon lloc, pot ocórrer que no existeixi aleshores, a és una…
anàlisi no estàndard
Matemàtiques
Branca de la lògica matemàtica que fonamenta un càlcul amb infinits i infinitèsims a l’estil de Leibniz.
Hom obté un model no estàndard *R del cos R dels nombres reals com a ultrapotència de R *R és un cos ordenat no arquimedià que conté R i d’altres elements infinitament grans i infinitament petits Per a alguns problemes pot ésser més senzill treballar a *R que no pas a R En tot cas permet una formulació diferent de la pròpia del mètode de Weienstrass amb ε i δ, que pot ésser més intuïtiva Fou desenvolupada per A Robinson a partir del 1960