Resultats de la cerca
Es mostren 6627 resultats
forma
Matemàtiques
Aplicació f d’un espai vectorial E de n dimensions en el cos K d’escalars en el qual és definit i que generalment és el cos dels nombres reals o dels nombres complexos.
Segons quin sigui el valor de n i les propietats de f , hom distingeix diversos tipus de formes Hom diu que f és una forma lineal o funcional lineal si, per a x i y de E i λ de K, f satisfà f x+y = f x + f y i f λ x = λ f x El conjunt de formes lineals d’un espai vectorial E sobre el seu K , és E* , espai dual Si hom pot considerar E com a producte cartesià de n espais vectorials, una forma f transforma tot conjunt ordenat de n vectors en un escalar de K si aquesta f , en ésser restringida a un vector qualsevol,…
Els sifonàpters: puces
Característiques de grup Les dimensions de les puces oscillen generalment entre 1 i 6 mm, dimensions extremes que poden ésser illustrades en el cas d’aquestes dues espècies, Echidnophaga murina a l’esquerra, un mascle i Hystrichopsylla talpae subespècie talpae a la dreta, un mascle Les femelles són sempre més grosses que els mascles Jean Claude Beaucournu / Henri Launay Els sifonàpters, anomenats genèricament puces, són insectes petits d’1 a 6 mm, generalment, aplatats lateralment, i mancats d’ales àpters La característica que els ha fet més coneguts és la seva capacitat de saltar i el seu…
teorema de Schwarz
Matemàtiques
Teorema referit a una funció real f de dues variables reals, f: ℝ2 → ℝ.
Afirma que si existeixen les derivades primeres ∂ f /∂ x i ∂ f /∂ y en un entorn U d’un punt x 0 , y 0 , i existeix la derivada segona ∂ 2 f /∂i> x∂ y i és contínua en el punt x 0 , y 0 , aleshores existeix la derivada segona ∂ 2 f /∂ y ∂ x al punt x 0 , y 0 i se satisfà que ∂ 2 f /∂ x ∂ y x 0 y 0 = ∂ 2 f / ∂ y ∂ xx 0 , y 0 El teorema de Schwarz és una simplificació del teorema de Bonnet
polinomis de Legendre
Matemàtiques
Polinomis en ℝ donats per l’expressió genèrica
.
Satisfan la fórmula de recurrència n +1 P n + 1 x - 2n+1 P n x + nP n - 1 x =0, i són solucions de l' equació diferencial de Legendre , 1- x 2 y´´ - 2 xy ´ + n n +1 y = 0 Els primers polinomis són P 0 x = 1, P 1 x = x , P 2 x = 3 x 2 -1 /2 Satisfan la següent ortogonalitat on és el símbol de Kronecker
vector
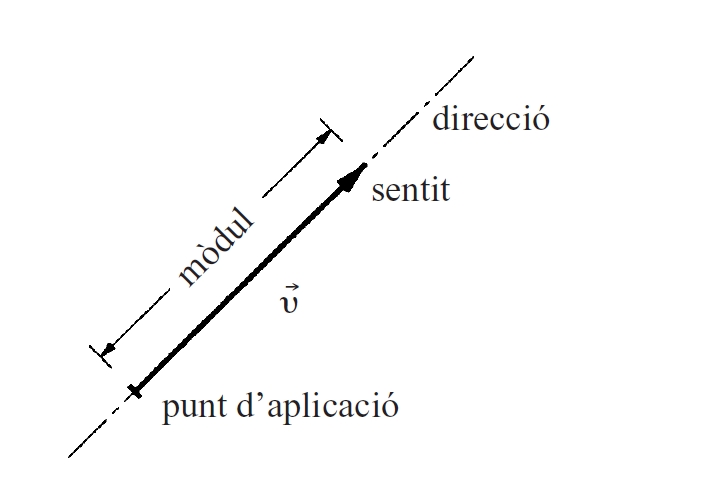
Vector
Física
Matemàtiques
Element d’un espai vectorial.
Des del punt de vista geomètric, a tot vector se li pot associar direcció, mòdul i sentit, i un punt d’aplicació Segons les seves posicions relatives, es parla de vectors simètrics, oposats, conjugats, ortogonals, etc Fixada una base de vectors e 1 ,, e n en un espai vectorial E de dimensió n base d’un espai vectorial, tot vector x de E pot ésser expressat en forma única com a combinació lineal dels elements de la base x = x 1 e 1 + + x n e n Així, x resta determinat pels nombres x 1 , x 2 ,, x…
àlgebra tensorial
Matemàtiques
És, dins de l’àlgebra abstracta, una construcció d’una àlgebra associativa T(E) partint d’un espai vectorial V.
Sigui E un espai vectorial sobre un cos commutatiu K , per a cada parella p , q de nombres naturals, existeix una aplicació bilineal única T pq de T p E X T q E en T p+q E tal que, per a tot element x 1 ,, x p d’ E p i tot element x p+1 ,, x p+q d’ E q , T pq x 1 OOOoooOOO x p , x p+1 OOOoooOOO x p + q = x 1 OOOoooOOO x p+q , on T n E és la potència tensorial n -èsima d E Les aplicacions bilineals T pq defineixen sobre l’espai…
recta tangent

recta tangent a una corba en un punt
Matemàtiques
Recta que passa per un punt P d’una corba o d’una superfície i és la posició límit d’una recta variable que passa per aquest punt i per un altre de la mateixa corba o superfície que es mou fins a coincidir amb el primer.
Si l’equació de la corba plana és y = f x , la tangent en el punt P x 0 , f x 0 és la recta y-f x 0 = f' x 0 x-x 0
Michael Phelps

Michael Phelps (2013)
© Jamie McDonald/Getty Images For Laureus
Natació
Nedador nord-americà.
A 15 anys fou el component més jove de l’equip olímpic dels EUA a Sydney 2000 des del 1932, i l’any següent esdevingué el recordista més jove de la història, en la prova dels 200 m papallona El 2001 aconseguí batre el seu primer rècord mundial en 200 m papallona, i fins al desembre del 2009 n'aconseguí fins a 39, 29 dels quals eren individuals la majoria en les especialitats de papallona i estils, però també en la d’estil lliure i 10 en relleus, de manera que superà àmpliament els 33 de Mark Spitz Després de les Olimpíades de Londres agost del 2012 es va retirar de l’alta competició,…
funcions de Bessel de primera classe
Matemàtiques
Solucions de l’equació diferencial de Bessel, de la forma
on Γ és la funció gamma.
J - n x n’és també una solució particular Si n és un nombre enter J - n x = -1 n J n x en canvi, si n no és enter J n x i J - n x són independents, de manera que la solució general de l’equació diferencial de Bessel és y x = aJ n x + bJ - n x ,en què a i b són constants
polinomis d’Hermite
Matemàtiques
Polinomis en ℝ donats per l’expressió genèrica
Satisfan la fórmula de recurrència H n + 1 x - 2 xH n x + 2 nH n - 1 x = 0, i són solucions de l' equació diferencial d’Hermite, y n - 2 xy + 2 ny = 0 Els primers polinomis són H 0 x = 1, H 1 x = 2 x , H 2 x = 4 x 2 -2, etc Satisfan la següent ortogonalitat on δ p q és el símbol de Kronecker
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- …
- Pàgina següent
- Última pàgina