Resultats de la cerca
Es mostren 97 resultats
funció sumable
Matemàtiques
Funció tal, que la seva integral de Lebesgue existeix.
Per exemple, si f és una funció real de variable real fitada M fita superior i m fita inferior en un interval Ω, f és sumable si existeix el límit únic anotat ∫ Ω f x dx de on { a o = m , a ₁, a ₂, , a n = M } és una partició qualsevol de l’interval m, M que s’apropa a grandària zero per a n gran | a i - a i-1 | → 0 i e i = { x | a i-1 | ≤ f x ≤ a i } és un conjunt mesurable existeix l e₁ segons la mesura de Lebesgue
funció monòtona a trossos
Matemàtiques
Funció f: [a,b]⊂ℝ→tal que existeix una subdivisió del seu interval de definició, a = a0 <a1 <... <an = b, tal que, per a tot i=1,...
< a n = b , tal que, per a tot i =1,, n , existeix una funció f i monòtona en l’interval tancat a i - 1 , a i i igual a en l’interval obert a i - 1 , a i
funció contínua a trossos
Matemàtiques
Funció f:[a,b]⊂ℝ→ℝtal que existeix una subdivisió del seu interval de definició, a=a0 <a1 <...<an =b, tal que, per a tot i=1,...
, n , existeix una funció f i contínua en l’interval tancat a i - 1 , a i i igual a f en l’interval obert a i - 1 ,a i Les discontinuïtats de són discontinuïtats de primera espècie discontinuïtat
punt de retrocés
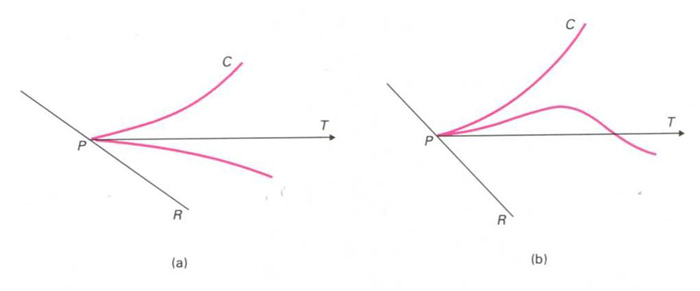
Punt de retrocés de primera (a) i de segona (b) espècie
© fototeca.cat
Matemàtiques
Donada una corba plana C
, punt P
d’aquesta corba en el qual existeix una tangent T
de tal manera que existeix un entorn U
de P
i una recta R
, diferent de T
, tals que els punts de C ∩U
pertanyen al mateix semiplà respecte a R
.
És un punt de retrocés de primera espècie si existeix un entorn U´ de P tal que els punts de C ∩U´ són repartits entre els dos costats de T , i és un punt de retrocés de segona espècie si són al mateix costat respecte a T Un punt de retrocés és anomenat també cúspide o punt cuspidal
derivada direccional d’una funció en un punt
Matemàtiques
Donada una funció D ⊂ℝ n →ℝ, un punt a∈D, i un vector no nul v∈ℝ n , límit, si existeix, del quocient [f( a+h v) - f( a)]/h, quan h tendeix a zero.
Si aquest límit existeix hom el nota per f ´ a , v , i hom diu que f és derivable en la direcció v en el punt a i que f ´ a , v és la derivada de f en la direcció en el punt a Les derivades parcials són derivades en la direcció dels vectors unitaris canònics de ℝ n
teorema de Rolle
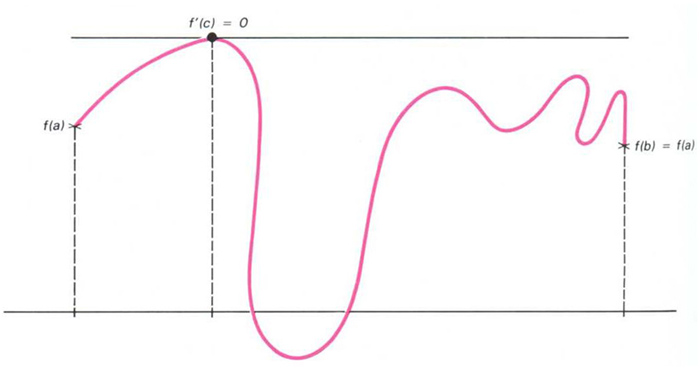
Teorema de Rolle
© fototeca.cat
Matemàtiques
Teorema segons el qual si f és una funció contínua en tots els punts d’un interval tancat [a,b] i té derivada en cada punt de l’interval obert (a,b), aleshores si f (a) = f (b), existeix un punt c en (a,b) tal, que f´ (c) = 0.
És a dir, existeix una tangent horitzontal a la corba representativa de la funció en un punt c , entremig de a i b
derivada d’una funció en un punt
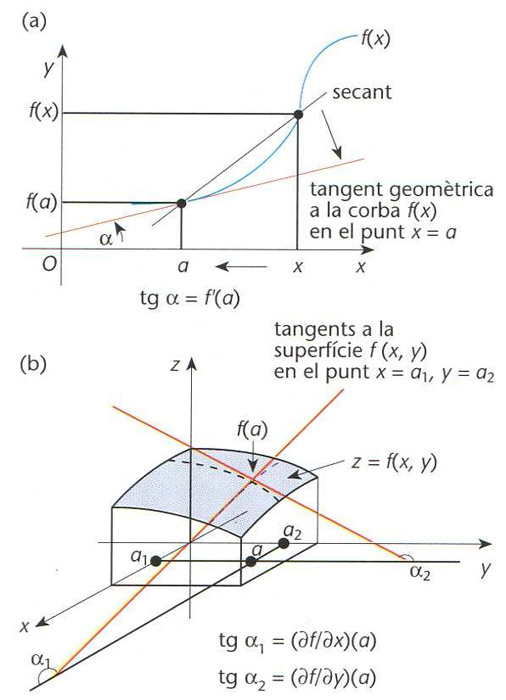
Interpretació gràfica de la derivada d’una funció (a) i de les derivades parcials d’una funció de dues variables (b); en (a), tgα = f' (a); en (b), tgα1 = ϑf/ϑx (a) i tgα2 = ϑf/ϑy (a)
© fototeca.cat
Matemàtiques
Donada una funció f: D⊂ℝ→ℝ i un punt del seu domini de definició, a ∈D, límit, si existeix del quocient [f(x) — f(a)]/(x-a) quan x tendeix a a tot mantenint-se a l’interior de D.
Quan aquest límit existeix, hom diu que la funció f és derivable en a , i el límit és notat per f´ a , df/dx a o Df a , i hom l’anomena derivada de f en el punt a Hom diu que f és derivable en un cert domini S si ho és a cada punt de S Aleshores, la funció f´ x que assigna a cada punt a ∈ S la derivada de f en a és anomenada funció derivada de f o, simplement, derivada de f Si f´ x és, al seu torn, derivable en un cert domini T , hom pot definir-n'hi la derivada, que és la derivada segona de f, f´´ x Hom procedeix consecutivament per tal de definir les derivades d’…
quantificador
Matemàtiques
Qualsevol dels símbols que, en l’escriptura formal, precedeixen les funcions proposicionals.
Els més coneguts són per a tot x ∀ x quantificador universal existeix x ∃ x quantificador existencial Una frase com “existeix un home que és odiat per tots els homes” podria ésser formalitzada per ∃ x /∀ y x és odiat per y L’ús dels quantificadors és degut a Frege 1879 El símbol ∃d’existència és degut a Peano 1894, i el ∀, a Hilbert
funció holomorfa
Matemàtiques
Funció f
: U
⊂ℂ→ℂque té la propietat d’holomorfia.
La funció f definida sobre l’obert U és holomorfa en el punt z 0 ∈ U si és derivable en z 0 , és a dir, si existeix el límit La funció f és holomorfa en un obert U si és holomorfa en tot punt de U La funció f és holomorfa a l’infinit si existeix un nombre real positiu a tal que, per a tot z ∈ℂque verifiqui | z |> a, f és holomorfa en z
categoria
Matemàtiques
Estructura algèbrica composta per una família d’objectes matemàtics i per una família de morfismes entre aquests objectes, tal que satisfà les següents propietats.
per a tot parell X,Y d’objectes de la categoria existeix un conjunt Hom X,Y, anomenat conjunt de morfismes de X en Y, tal que HomX,Y = HomX’,Y’ si i només X=X’ i Y=Y’ i, per a tot triplet X,Y,Z d’objectes de la categoria, existeix una aplicació Hom Y,Z x HomX,Z→HomX,Z, anomenada composició de morfismes, que satisfà l’associativitat i l’existència d’una identitat a cada HomX,X és a dir, existeix un morfisme 1 x tal que per a tot f de HomX,X se satisfà Els objectes d’una categoria no han de formar necessàriament un conjunt, sino una classe així, per…
Paginació
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- …
- Pàgina següent
- Última pàgina