Resultats de la cerca
Es mostren 10 resultats
el·lipsoide
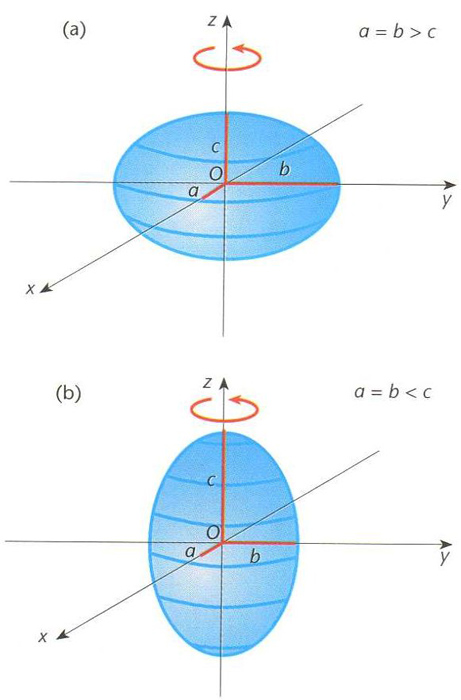
El·lipsoide aplatat (a) i allargat (b) obtinguts per rotació d’una el·lipse, prenent com a eix de la rotació el que conté, en el primer cas, el semieix menor d’aquesta el·lipse i, en el segon, el semieix major
© Fototeca.cat
Matemàtiques
Superfície de segon grau o quàdrica amb centre l’equació de la qual és (
x 2
/a 2
)+(
y 2
/b 2
)+(
z 2
/c 2
)=1 si els eixos de coordenades són els propis de la quàdrica.
Una ellipse que giri al voltant del seu eix menor determina un ellipsoide aplatat , anomenat també esferoide oblat i una ellipse que giri al voltant del seu eix major determina un ellipsoide allargat , anomenat també esferoide prolat Quan a=b=c=r l’ellipsoide esdevé una esfera de radi r
quadrant
Matemàtiques
Cadascuna de les quatre parts en què un pla és dividit per dos eixos de coordenades rectangulars.
Són anomenats primer, segon, tercer i quart quadrant , prenent com a primer el superior de la dreta i comptant-los en el sentit antihorari
regla de L’Hôpital
Matemàtiques
Regla que permet de calcular límits de funcions en el cas d’indeterminacions del tipus 0/0 o ∞/∞.
Segons aquesta regla, el límit del quocient de dues funcions és igual al quocient de llurs derivades, o sia Si el quocient entre les primeres derivades continua essent indeterminat, hom aplica la regla prenent les segones derivades, i així successivament, fins a resoldre la indeterminació
Jean François Fernel
Jean François Fernel
© Fototeca.cat
Astronomia
Matemàtiques
Matemàtic, astrònom i metge francès.
Fou nomenat metge de cambra d’Enric II 1547 Introduí diferents termes en fisiologia i patologia i determinà l’apendicitis i el peristaltisme 1542 Féu la primera descripció de l’endocarditis, i en termes generals, a part els seus tractats de matemàtiques i d’astronomia, establí un nou criteri en medicina prenent com a base la medicina de Galè i la medieval
nombre complex
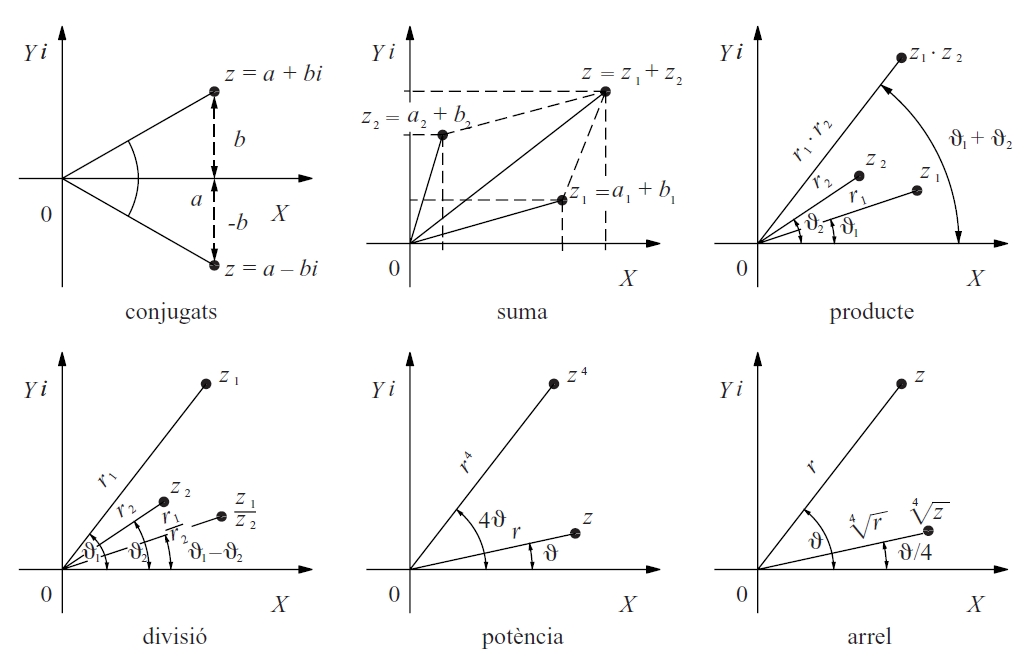
Nombres complexos
Matemàtiques
Nombre que pot ésser expressat com a suma d’un nombre real i d’un nombre imaginari.
Hom construeix el conjunt ℂ dels nombres complexos afegint al conjunt dels nombres reals un nombre nou, no real, que hom representa per una i , i que és definit formalment per la propietat que el seu quadrat és -1 Hom estén a aquest conjunt ℂ les operacions d’addició i de multiplicació amb totes les propietats que tenen entre nombres reals Cada nombre complex pot ésser escrit en forma de polinomi de primer grau en i , a + bi , i pot ésser representat geomètricament en el pla prenent a i b com a coordenades en un sistema cartesià ortogonal pla d'Argand-Gauss Aquesta correspondència entre els…
relació de proximitat
Matemàtiques
Relació binària S entre els subconjunts d’un conjunt E, que fou introduïda per Efremovič per tal de generalitzar la relació ‘‘ésser pròxim’’ que hom utilitza correntment en l’espai mètric ordinari.
La relació de proximitat és definida pels axiomes següents ASB ⇔ BSA , és a dir, la relació S és simètrica ASB ⇒ A ≠∅i B ≠∅, és a dir, el conjunt buit no és pròxim a cap altre AS B ∪C ⇒ ASB o ASC , és a dir, un conjunt és pròxim a la reunió de dos conjunts si és pròxim, almenys, a un d’ells A ∩B ≠∅⇒ASB , és a dir, dos conjunts que es tallen són pròxims { X } S { Y } ⇔ X=Y , és a dir, un punt només és pròxim a si mateix si A$B aleshores existeix un conjunt C tal que B$C i A$C c , on C c és el conjunt complementari de C Tota proximitat indueix una topologia prenent com a…
relació d’equivalència
Matemàtiques
Relació binària entre els elements d’un conjunt que permet d’establir una classificació d’aquests elements de tal manera que resti cadascun en una classe, dita d’equivalència, i aquestes classes no tinguin cap element comú.
Perquè una relació sigui d’equivalència cal que sigui reflexiva, simètrica i transitiva relació Tota relació d’equivalència estableix una classificació del conjunt i tota classificació determina una relació d’equivalència Són equivalents dos elements que pertanyen a la mateixa classe El conjunt de les classes considerada cadascuna com un nou element és anomenat conjunt quocient del conjunt de partida C per a aquesta relació R , i s’escriu C/R Una aplicació d’un conjunt en un altre determina una relació d’equivalència entre els elements del conjunt original, prenent com a …
volum
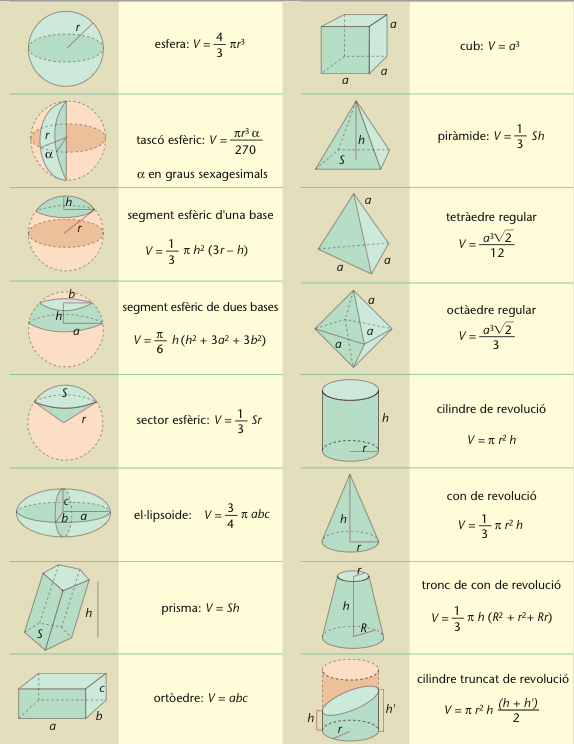
Fórmules per al càlcul de volums
© Fototeca.cat
Matemàtiques
Grandor o mesura de la porció de l’espai ocupada per un cos.
El volum és una mesura que a tota regió de l’espai de tres dimensions assigna un nombre real positiu, de manera que es compleix la propietat additiva, és a dir, que el volum d’un cos és igual a la suma dels volums de qualsevol partició que hom hagi fet en el cos divisió del cos en parts disjuntes Prenent com a base que el volum assignat a un cub de costat a és a 3 , el volum de qualsevol altre cos pot ésser calculat com l’ínfim de la suma dels volums dels cubs disjunts que plegats cobreixen el cos Així, el volum d’una figura plana és zero El volum dels cossos geomètrics simples pot ésser…
teorema de Ceva
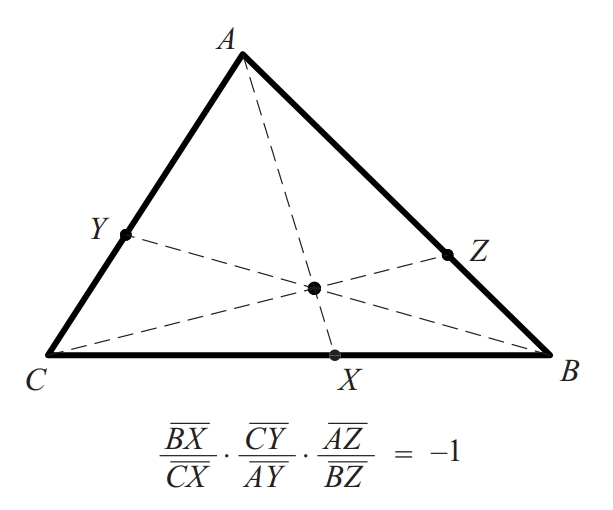
teorema de Ceva
Matemàtiques
Teorema segons el qual, prenent tres punts X, Y i Z sobre els costats (si cal, prolongats) BC, CA i AB d’un triangle de vèrtexs A, B i C, les rectes AX, BY i CZ són concurrents si, i solament si, (BX ⁄ CX) · (CY ⁄ AY) · (AZ ⁄ BZ) = –1.
Aquesta condició equival al fet que el producte de les tres raons simples valgui –1 X , A , B Y , B , C Z , C , A = –1 Aquest teorema és dual del teorema de Menelau
regressió
Matemàtiques
Estudi de la millor aproximació d’una variable estadística y a partir d’una família donada de variables estadístiques x1..., xn, mitjançant combinacions lineals del tipus a1 x1..., an xn + b, i prenent com a criteri de “millor aproximació” el del mètode dels mínims quadrats.
Dit d’una altra manera, cal cercar els anomenats coeficients de regressió a 1 , a 2 , , a n , b , tals que facin mínima la distància al quadrat d 2 y, a 1 x 1 + + a n x n +b Si hom representa els valors de les variables estadístiques en l’espai ℝ n + 1 , aleshores l’hiperplà y = a 1 x 1 + + a n x n + b és dit de regressió per a n = 1, hom té la recta de regressió , i per a n = 2, el pla de regressió En el cas que n = 1, la recta de regressió y = ax + b té per coeficients on x i , y i són els valors de les variables, i x, y , les seves esperances o valors mitjans En el núvol de…