Resultats de la cerca
Es mostren 5896 resultats
Pere de Litala
Literatura italiana
Poeta sard, autor de Rime diverse (Càller, 1595), la primera obra sarda escrita en italià, llengua que adoptà després d’una estada a Còrsega i a Itàlia.
Xenofont d’Efes
Literatura
Novel·lista grec.
Pertany a la segona sofística La seva obra, Efesíaques , narra les tribulacions d’un matrimoni jove separació, naufragis, ambients de lladres, esclavatge, etc Àntia i la seva muller Habrocoma es mantenen fidels a la seva promesa fins que es retroben i poden tornar a Efes La caracterització dels personatges és pobra Conté testimoniatges importants sobre la vida religiosa d’Efes L’obra fou traduïda al català per Carles Miralles per a la Fundació Bernat Metge 1967
Pere Ribera de Perpinyà
Lingüística i sociolingüística
Historiografia catalana
Cronista català conegut també com Pere Ribera de Perpejà, per mala interpretació d’un passatge de Nicolàs Antonio.
Vida i obra Traduí les obres historiogràfiques de Rodrigo Jiménez de Rada, arquebisbe de Toledo Gràcies a una anotació d’un manuscrit d’El Escorial, avui perdut, transcrita a mitjan segle XVII per Nicolás Antonio, sabem que el 1266 traduí al català la Historia Arabum Coetàniament, o poc temps després, es degueren traduir les altres obres del toledà La raó és que, per una banda, Jiménez havia conclòs el De rebus Hispaniae on, per primer cop, el terme Hispània ja no es limitava a al-Àndalus, sinó que s’estenia al conjunt de la península Ibèrica, i, per l’altra, l’arquebisbe havia mantingut…
, ,
Francesc Jordana

Francesc Jordana
Arxiu F. Jordana
Bàdminton
Entrenador i àrbitre de bàdminton.
Començà com a tècnic a l’Escola Anna Mogas de Granollers 1988 i al Club Casino La Garriga 1989 Cursà el títol d’àrbitre nacional i d’entrenador a la Gran Bretanya Fou responsable de formació i cap dels jutges de línia dels Jocs Olímpics de Barcelona 1992 Prosseguí la formació com a entrenador a l’escola de la Federació Europea de Bàdminton 1994 També fou entrenador de l’Escola de Bàdminton de la UAB 1990-95, del Club de Bàdminton Bellaterra 1993-95, del Centre de Tecnificació de Bàdminton de la federació catalana 1996-2003, del Club Bàdminton Granollers 1996-2003 i responsable de l’Escola…
funció periòdica
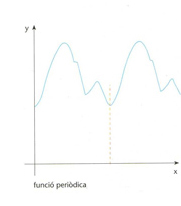
Funció periòdica
© Fototeca.cat
Matemàtiques
Funció f
: D
⊂ℝ→ℝtal que existeix un nombre T
∈ℝ-{0} que satisfà que, per a tot x
∈ D, x
+ T∈ D
i f
( x
+ T
)= f
( x
).
Hom diu aleshores que T és un període de la funció f bé que hom anomena, pròpiament, període al més petit nombre T que satisfà les condicions esmentades En són exemples les funcions trigonomètriques sinus i cosinus que tenen un període 2π
gradient
Física
Matemàtiques
Donada una funció f
derivable i definida en una regió de l’espai ℝ 3
, funció vectorial (grad f
o ∇ f
) definida per la fórmula
.
En cada punt, és un vector perpendicular a la superfície f = constant, que passa pel punt en què és calculat, i, per tant, té la direcció en la qual varia més ràpidament Per extensió, hom anomena gradient d’una funció en una direcció o derivada direccional la projecció del vector gradient en aquella direcció Així, fixada una direcció, el gradient d’una funció en aquella direcció dóna el ritme de variació de la funció en avançar en la direcció considerada En meteorologia i en física de fluids són molt utilitzats els gradients tèrmics i baromètrics per a referir-se a les…
càlcul de diferències
Matemàtiques
Estudi de les propietats d’una funció de la qual hom només coneix un conjunt finit de valors f(x0), f(x1), ..., f(xn), que corresponen als arguments x0, x1, ..., xn, els quals, habitualment, són presos en progressió aritmètica xr=x0+rϖ.
Hom defineix l’ operador diferència Δ, mitjançant l’expressió Δf x = f x + ϖ - f x , i l’ operador incremental E , definit per E ϖ f x = f x + ϖ = f x + Δ f x , de manera que E = 1+Δ Les propietats d’aquests permeten d’assolir el resultat següent, dit teorema de Gregory f x + nϖ = E nϖ f x = 1+Δ n f x , on, en l’última expressió, hom pot emprar la fórmula del binomi de Newton Aquests operadors poden expressar les diferències dividides Hom pot obtenir una…
nombres de Fermat
Matemàtiques
Nombres, Fn, definits per l’expressió (per a n = 1,2,3,...).
El 1640 Fermat cregué que aquests nombres eren primers, però l’any 1740 Euler donà una descomposició per a F 5 = 4 294 967 297, com a producte de 641 per 6 700 417, i posteriorment hom ha demostrat que per a n tal que 5 ≤n≤17 , F n no és primer, i que d’altres nombres de Fermat, com F 1 9 4 5 , F 3 3 1 0 i F 6 5 3 7 són descomponibles El 1796 Gauss demostrà que els únics polígons regulars que hom pot construir amb regle i compàs són els que tenen un nombre de Fermat de costats
mínim relatiu
Matemàtiques
Valor que pren una funció f(x) en un punt x=a quan aquest valor és menor que els valors de f(x) en els punts immediatament anteriors i posteriors al punt a.
És anomenat també mínim local , i en el cas particular que existeixen les derivades successives de f x es compleix que en el punt a la primera derivada f ' a és nulla i la segona, f ' a , normalment és positiva En el cas, però, que tant f ' a com f ' a siguin nulles, la condició que f x tingui un mínim en el punt a és que la primera derivada de f x no nulla en el dit punt sigui d’ordre parell i positiva Aquestes són les condicions que hom aplica per a trobar els mínims d’una funció
sèrie trigonomètrica
Matemàtiques
Cadascuna de les sèries de funcions Σfi , amb fi (x) = an cos nx + bn sin nx
.
Hom demostra que si una sèrie trigonomètrica convergeix uniformement per a x ∈ -π,π la funció f cap a la qual convergeix és contínua i periòdica amb període 2π, i que els coeficients a n , b n s’hi relacionen
Paginació
- Primera pàgina
- Pàgina anterior
- …
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- …
- Pàgina següent
- Última pàgina