El llenguatge de les matemàtiques

La matemàtica com a llenguatge

L’escrit que us presentem a continuació són els deures d’un noi rus. ¿Podeu endevinar quin exercici li ha demanat el seu professor de matemàtiques perquè el faci a casa?

Es tracta, com pot deduir algú que tingui una mínima noció de matemàtiques, de la resolució d’una equació de primer grau. Però, si no entenem el rus, ¿com podem entendre el tema a què es refereixen les operacions escrites més amunt? Doncs perquè estan escrites en un llenguatge compartit per nosaltres amb els nois russos. Aquest llenguatge, que tenen en comú els joves de tot el món anomenat civilitzat, és el llenguatge de les matemàtiques. En podem tenir la prova observant el mateix exercici escrit per un noi català i per un d’anglès:

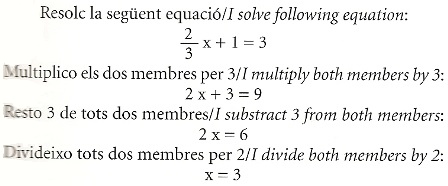
Aturem-nos un moment a reflexionar sobre aquests punts: a) Les matemàtiques són un veritable llenguatge; b) Aquest llenguatge és internacional: les explicacions canvien d’una llengua a l’altra, mentre que les fórmules matemàtiques es mantenen invariables; c) El llenguatge matemàtic és més internacional que l’alfabet: els russos, els àrabs i els xinesos, que no fan servir el nostre alfabet, també escriuen les fórmules com nosaltres. En els llibres en àrab, per exemple, mentre que les ratlles escrites es llegeixen de dreta a esquerra, les fórmules es llegeixen d’esquerra a dreta, com les nostres; d) És un llenguatge simbòlic, que s’utilitza per a representar per escrit conceptes abstractes, idees generals sobre la quantitat, la mesura, la forma d’allò que ens envolta, i les relacions que vinculen aquests conceptes entre ells.

Vegem ara quins són els elements que constitueixen un llenguatge. En primer lloc considerem les paraules i la manera de representar-les. Com sabem, i com es pot veure en els exemples posats més amunt, no tots els pobles utilitzen els mateixos signes per a escriure. Però hi ha una distinció prèvia encara més important. No tots els pobles utilitzen les mateixes convencions per a escriure les seves idees. Així, els xinesos encara fan servir els ideogrames, com feien els antics egipcis; per això, la seva escriptura conté moltíssims signes (més de 6 000), i cada concepte bàsic es representa amb un sol ideograma sil·làbic, mentre que la resta de conceptes s’escriuen amb dos o més ideogrames. Els russos, en canvi, empren les mateixes convencions que nosaltres, és a dir, formen les paraules combinant signes que representen sons, que són les lletres de l’alfabet, però utilitzen lletres diferents de les nostres i el seu alfabet té més lletres que no pas el nostre. Ara bé, quins són els signes i les convencions del llenguatge matemàtic?

Les xifres i la representació dels nombres enters

Quan es comença a estudiar una llengua escrita, primer de tot se n’aprenen les lletres de l’alfabet i les regles per a combinar-les a fi de formar paraules. En el llenguatge de les matemàtiques, l’alfabet és constituït pels signes gràfics que s’usen per a representar el sistema de numeració, és a dir, les xifres. Els nombres es poden considerar en matemàtiques com les paraules d’una llengua.

Representació dels nombres enters en base 10

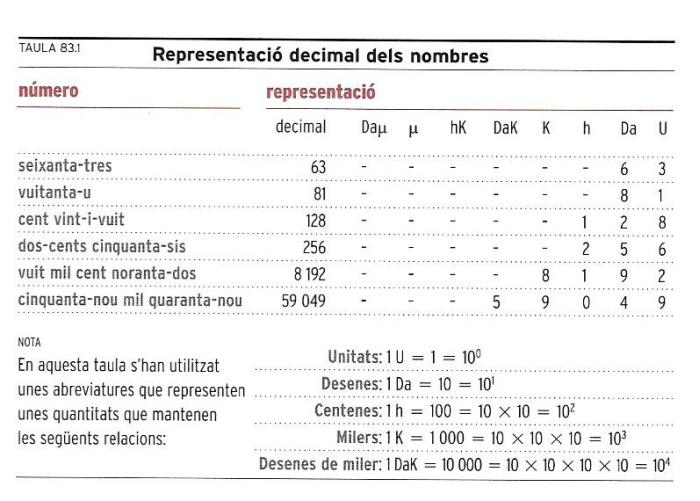
Quadre 83.1 Representació decimal dels nombres.

ECSA

L’alfabet dels nombres que avui s’utilitza arreu del món va ser introduït a Europa pels àrabs fa gairebé mil anys. Les “lletres” d’aquest alfabet són les anomenades xifres aràbigues, és a dir, els números 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9.

Per a combinar i escriure els nombres s’utilitzen les regles que vam aprendre de petits a l’escola, la primera de les quals ens diu que les xifres 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9 tenen valors diferents segons que es trobin a la columna de les unitats, de les desenes, de les centenes, etc. Sabem molt bé, per exemple, que el número 278 (dos-cents setanta-vuit) representa 2 centenes, 7 desenes i 8 unitats. També sabem que en el número 278 el 2 val molt més que el 7, i que el 7 val més que el 8, perquè el 2, col·locat en aquesta posició, val 200, mentre que el 7, en la posició que ocupa aquí, val 70, i el 8, que és en la posició de les unitats, només val 8.

Quadre 83.2 Representació dels nombres en base 10.

ECSA

Com que les xifres tenen un valor diferent segons la posició que ocupen en el nombre, es diu que, en la numeració aràbiga, tenen un valor posicional. Aquesta és una convenció molt important, que permet escriure qualsevol nombre enter, que pot ser elevadíssim, utilitzant solament deu signes diferents. Per això aquesta manera d’escriure els nombres s’anomena representació decimal o representació en base 10.

Ara mirarem d’escriure una fórmula que resumeixi el que hem dit i que ens permeti representar en base 10 qualsevol nombre. Primer de tot considerem alguns exemples, que hem agrupat al quadre 83.1, “Representació decimal dels nombres”. Observant l’explicació al peu d’aquest quadre veiem que per a escriure una unitat es pot escriure 1 x 100, per a escriure una desena es pot escriure 1 x 101, etc. Per a escriure un milió es podria escriure 1 x 106; i dos milions, 2 x 106. Dos milions més tres unitats s’escriuria 2 x 106 + 3 x 100. Així, els nombres del quadre 83.1 també es poden escriure de la manera indicada en el quadre 83.2, “Representació dels nombres en base 10”.

Suposem que volem representar un nombre qualsevol, format per c0 unitats, c1 desenes, c2 centenes, c3 milers, etc., en què c0, c1, c2, c3... són les lletres utilitzades com a abreviacions per a indicar respectivament:

c0 = nombre de les unitats, és a dir, nombre que es multiplica per 100;

c1 = nombre de les desenes, és a dir, nombre que es multiplica per 101;

c2 = nombre de les centenes, és a dir, nombre que es multiplica per 102;

c3 = nombre dels milers, és a dir, nombre que es multiplica per 103;

i així successivament.

La representació decimal d’aquest nombre qualsevol tindrà la forma següent:

ck x 10k + ck–1 x 10k–1 + ... + c1 x 101 + c0 x 100 [1]

Aquesta expressió s’anomena fórmula, i també pertany al llenguatge de les matemàtiques, però és una cosa molt més complexa que allò de què hem parlat fins ara.

Es podria dir que, mentre que les xifres que representen els nombres són l’alfabet de les matemàtiques, aquesta fórmula, que sintetitza la representació decimal de qualsevol nombre, pertany a la sintaxi de la matemàtica. En continuarem parlant més endavant. De moment, notem només que mitjançant la fórmula [1] es pot representar un nombre qualsevol, tan sols cal atribuir uns valors numèrics determinats a cada lletra que hi figura.

Representació d'un nombre enter en qualsevol base

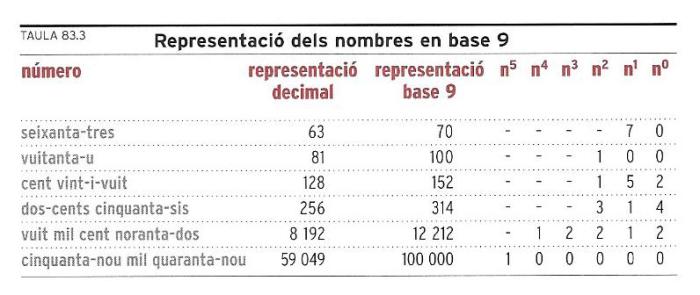
Quadre 83.3 Representació dels nombres en base 9.

ECSA

Entretinguem-nos ara una mica amb l’alfabet dels nombres i amb la convenció del valor posicional, i veurem quines coses es poden fer! Comencem suposant que el nostre processador de textos no permet escriure el número 9. Així, com que el 9 ha desaparegut, només ens queden els números 0, 1, 2, 3, 4, 5, 6, 7 i 8. Però, com ens ho farem ara per a escriure tots els nombres?

Utilitzem també la convenció del valor de posició. Les xifres que tenim ens permeten escriure les unitats fins a 8; quan arribem al número 9, escrivim 10 (que es llegeix: “un, zero”). Aquest cop l’1 no està representant una desena, sinó una “novena”, és a dir, un paquet de nou elements, això és, el número 9. Aleshores l’11 representa el número que segueix el 9, és a dir, el 10; el 12 representa el número que segueix el 10, és a dir, l’11, i així successivament. Per tant, el número 17, l’escriurem 18; però, i el 18, com escriurem el número 18? Com que no disposem de la xifra 9, haurem de pensar en alguna possible solució. Així, optem per:

divuit = 20 = 2 novenes = 2 x 9 + 0

dinou = 21 = 2 novenes + 1 = 2 x 9 + 1

vint = 22 = 2 novenes + 2 = 2 x 9 + 2

vint-i-sis = 28 = 2 novenes + 8 = 2 x 9 + 8

vint-i-set = 30 = 3 novenes + 0 = 3 x 9 + 0

vint-i-vuit = 31 = 3 novenes + 1 = 3 x 9 + 1

Tindrem nombres de dues xifres fins al vuitanta, que s’escriurà: vuitanta = 88 = 8 novenes + 8 = 8 x 9 + 8; després, es passarà al vuitanta-u, que s’escriurà: vuitanta-u = 100 = 1 novena de novenes = 1 x (9 x 9) + 0 x 9 + 0.

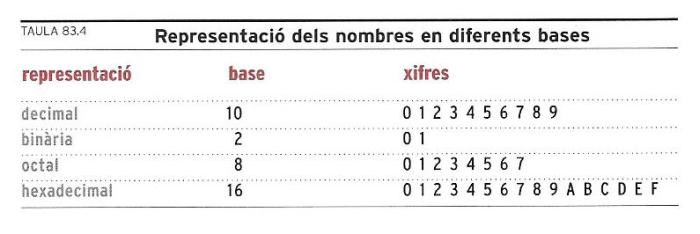
Quadre 83.4 Representació dels nombres en diferents bases.

ECSA

En el quadre 83.3, “Representació dels nombres en base 9”, es mostren els mateixos nombres del quadre 83.1, però escrits sense utilitzar el número 9 i fent servir l’estratègia de les novenes. Com que no existeixen símbols que en base 9 indiquin les novenes i les successives potències de 9, en aquest quadre hauríem hagut d’escriure a dalt de la columna de les unitats “nou elevat a zero”; a dalt de la columna de les novenes, “nou”; i després, “nou 2 nou = nou2”, “nou3”, etc. Però hem decidit abreujar l’escriptura en n0, n1, n2, n3, etc. fins a n5, que és “nou5” i que és la màxima potència de nou que hem considerat.

Aleshores, per a escriure un nombre qualsevol en base 9 podrem emprar una fórmula semblant a la fórmula [1], però en lloc del número10 hi haurà el número 9, que representem per n:

ck x nk + ck–1 x nk–1 + ck–2 2 nk–2 +...+ c2 x n2 + c1 x n1 + c0 x n0 [2]

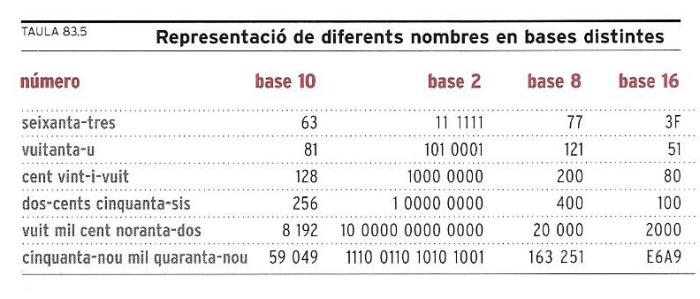
Quadre 83.5 Representació de diferents nombres en bases distintes.

ECSA

En aquesta fórmula, les lletres c encara representen els valors que les xifres poden adoptar, però ja no són deu, sinó nou, de manera que cada xifra c pot valer 0, 1, 2, 3, 4, 5, 6, 7 o 8. I aleshores, ja posats a fer, per què no diem que n, en comptes de significar 9, representa un altre nombre qualsevol? Així, la fórmula [2] es pot utilitzar per a representar un nombre qualsevol, escrit en una base qualsevol: n valdrà llavors el nombre escollit com a base, nk serà la seva potència k-èsima, i les xifres c seran tantes com val el número n.

El quadre 83.4, “Representació dels nombres en diferents bases”, inclou les bases més emprades, amb els noms respectius i els símbols que corresponen a les diverses xifres. És interessant observar que en el sistema hexadecimal, com que ha de tenir 16 xifres, es recorre a lletres de l’alfabet per a representar les xifres els símbols de les quals encara no s’han inventat. Així, A representa el número 10; B representa el número 11; C representa el 12; D, el 13; E, el 14; i F, el 15. Naturalment, el número 16 en base hexadecimal s’escriurà 10.

El problema d’escriure els nombres en bases diferents de la base 10 era, abans, quasi només un entreteniment divertit per a gent original. Des de feia segles tothom estava acostumat a operar amb la base10, perquè era com havien començat a fer-ho els primers éssers humans, que per a comptar no tenien més eines que els dits. La difusió dels ordinadors és el que ha fet importants les altres bases, bé que no totes, i no en el mateix grau. Les més utilitzades són les bases 2, 8 i 16, és a dir, les que representen potències de 2. El quadre 83.5, “Representació de diferents nombres en bases distintes”, inclou els nombres indicats a les taules 83.2 i 83.3, escrits en les bases més emprades.

Alguns jocs amb nombres enters

Ara, mirarem d’entretenir-nos una mica amb els nombres enters. El primer joc que us proposem, l’anomenem “Els pilons de mongetes”. Imaginem-nos la vida a l’antiguitat, fa un bon grapat de segles, i un noi que fa d’ajudant d’un ric comerciant. En aquell temps, els comerciants, per més rics que fossin, no eren persones socialment gaire importants, i les feines que havien de fer, com per exemple passar comptes, no eren considerades dignes de l’atenció dels savis; per això, no hi havia escoles que ensenyessin a comptar, i cadascú se les arreglava com podia.

Observem com se les empesca el jove ajudant per a comptar grans quantitats amb pilons de mongetes. Cada nombre seria un munt de mongetes, format per tantes mongetes com el valor del mateix nombre. Amb aquest sistema, el jove comptable compta en base 1, ja que disposa tantes mongetes com unitats té el nombre.

Tornant a la fórmula [2], es veu que també funciona per a n = 1; cal observar que aleshores nk= 1 per a qualsevol valor de k, i que les xifres ck tenen un sol valor possible, que podria tenir com a símbol, per exemple, la mongeta.

Ara imaginem-nos que ens posem en el lloc del noi i, desconcertats per la quantitat de mongetes que hem de comptar, mirem de trobar una manera senzilla per a anotar-ne el nombre. Agafem un pilonet de mongetes i fem el següent: a) Dividim el munt de mongetes en grups de deu mongetes cadascun. En sortirà un determinat nombre de grups, que no comptarem; en canvi, sí que comptarem el nombre de mongetes que ens en sobrin, amb les quals no es pot fer cap més grup complet de deu. Anotem bé aquest nombre. b) Apleguem els grups que han sortit de10 en 10; n’obtindrem un cert nombre, cadascun dels quals serà un piló de 100 mongetes. En sobraran unes quantes, de mongetes, sempre menys de cent. Anotarem també aquest nombre, i l’escriurem a l’esquerra del nombre ja registrat abans. c) Agrupem ara de 10 en 10 els grups de 100 mongetes, fent munts de 1 000 mongetes, doncs, i escrivim a l’esquerra del nombre que ja tenim a banda el nombre de grups de 100 que han sobrat. Podem continuar mentre ens quedin mongetes, és a dir, fins a registrar el nombre de l’última mongeta que n’hagi sobrat.

Si de debò fóssim el noi ajudant de l’antic ric comerciant, hauríem inventat la numeració en base 10, i hauríem passat a la història. Com que això no és així, ningú no ens priva de divertir-nos una mica amb el joc de les mongetes canviant el nombre de la base utilitzat per a fer pilons, cosa que ens permet obtenir nombres diferents en una base qualsevol. No passarem a la història, però és un exercici prou distret.

El segon joc proposat té un enunciat d’allò més simple: “És cert que dos i dos fan quatre?”. Algun cop hem sentit pronunciar a algú, en voler donar més força a una afirmació, una frase del tipus: “Això és així, com dos i dos fan quatre!”. Com més peremptori és el to de l’afirmació, més ganes vénen de preguntar-li: “En quina base?”. Aquesta pregunta desorientaria certament el nostre interlocutor aparentment tan segur d’ell mateix. En realitat, quasi sempre és veritat que 2 + 2 = 4, excepte en bases iguals o inferiors a 4, com per exemple en base 3, en què emprant només les xifres 0, 1 i 2 veiem que 2 + 2 = 11, ja que l’u és l’1, el dos el 2, el tres el 10 i el quatre l’11.

La gramàtica de la matemàtica: les operacions

Quan s’estudia una llengua, després d’haver après una mica l’ortografia i la fonètica d’algunes paraules es passa de seguida a l’estudi de la gramàtica, és a dir, del conjunt de regles per a combinar les paraules i formar frases correctes i entenedores.

És el mateix que passa en matemàtiques, on els nombres funcionen segons certes regles, que són les operacions. Així, un conjunt de nombres relacionats per un conjunt d’operacions s’anomena, precisament, expressió matemàtica. Una denominació interessant i fins i tot poètica a l’hora de parlar de nombres.

Els símbols de les operacions

Quadre 83.6 Símbols de les operacions fonamentals.

ECSA

Com s’ha dit, una operació és una regla que permet l’elaboració d’un o més nombres, és a dir, a partir d’uns elements, que anomenem operands, se n’obté un altre, que és el resultat de l’operació.

Cada operació és indicada per un símbol. Com passa amb l’escriptura dels nombres, els símbols de les operacions també són internacionals, com es pot observar en les fórmules de l’exemple inicial d’aquest article.

Amb tot, l’ús dels símbols de les operacions no és del tot estandarditzat, de manera que n’hi ha algunes que encara s’indiquen amb símbols diferents segons el context on s’utilitzen.

Com s’observa en el quadre 83.6, “Símbols de les operacions fonamentals”, les operacions que tenen símbols més estàndard són la suma i la resta, mentre que la multiplicació, malgrat que és una de les operacions més simples i més antigues, té un simbolisme menys definit absolutament. En les fórmules que hem vist fins ara hem utilitzat el símbol “2”, però n’hi ha d’altres. Els símbols d’operació són ideogrames, que representen de forma extremament sintètica conceptes prou enrevessats. Mirem, per exemple, de pensar com es podria explicar a un noi que ja coneix l’alfabet dels nombres la suma dels números 58 i 73. No és gens fàcil, però es podria començar dient-li: “Agafa una pila de 58 mongetes i una pila de 73 mongetes; ajunta totes dues piles i compta quantes mongetes hi ha en total. O bé agafa un collaret de 58 perles, i un altre collaret de 73 perles; agafa un fil llarg i fes un sol collaret amb totes les perles, i compta-les. O encara, posa 58 l de carburant en un dipòsit prou gran i després afegeix-n’hi 73 més; mira quants litres de carburant tens en total”.

Aleshores el noi entendria segurament el concepte d’addició i també s’adonaria que sumant 58 i 73 sempre s’obté 131, independentment del fet que se sumin mongetes, perles o litres de carburant.

És a dir, s’hauria adonat del significat de l’operació suma i de la seva homogeneïtat, això és, del fet que s’han de sumar grups d’elements del mateix tipus (mongetes amb mongetes, perles amb perles, litres de carburant amb litres del mateix carburant), i que el resultat representa un nombre d’elements també del mateix tipus (mongetes, perles o litres de carburant).

També es podria haver adonat de la propietat commutativa de la suma: el piló total de 131 mongetes es pot obtenir indiferentment afegint el piló de 73 al de 58 o viceversa; el collaret de 131 perles es pot obtenir indiferentment enfilant primer el de 58 i després el de 73 o viceversa; el nivell al dipòsit del carburant no varia en funció de l’ordre d’introducció dels 73 i els 58 litres. Però encara hauria d’aprendre moltes altres coses abans de saber totes les propietats expressades pel simple signe “+”.

El resultat de les operacions

Quan el noi del nostre exemple ho hagués après finalment tot sobre el signe “+” seria natural parlar-li de les altres operacions. Aleshores no seria difícil explicar-li les propietats de la multiplicació entre nombres enters i el significat dels símbols respectius. Però què passaria si, quan li expliquéssim l’operació resta, pretengués restar del piló de 58 mongetes el piló de 73? I si, quan li expliquéssim l’operació divisió, pretengués dividir el piló de 73 mongetes en 58 parts? Les pretensions del nostre alumne curiós són molt raonables des del punt de vista matemàtic; de fet, ens trobem davant el problema del tancament d’un conjunt numèric respecte d’una operació.

Es diu que un conjunt numèric és tancat respecte d’una operació quan el resultat de l’operació pertany al conjunt numèric al qual pertanyen els operands. Quan diem “conjunt numèric” volem dir el conjunt de tots els nombres possibles que tenen determinades característiques, com per exemple la propietat de ser enters.

El conjunt numèric a què ens hem referit fins ara és constituït pels enters positius més el zero. És l’anomenat conjunt dels nombres naturals, i en el llenguatge de les matemàtiques s’indica amb la lletra ℕ. El seu comportament respecte de les operacions considerades en el quadre 83.6, “Símbols de les operacions fonamentals”, és el següent:

— És tancat respecte de la suma; en efecte, sumant dos nombres naturals s’obté un nombre natural. Per a expressar aquesta propietat mitjançant els símbols del llenguatge matemàtic s’escriu: a, b ∈ ℕ → a + b ∈ ℕ.

— És tancat respecte del producte; en efecte, multiplicant dos nombres naturals s’obté un nombre natural. Amb símbols s’escriu: a, b ∈ ℕ → a · b ∈ ℕ.

— No és tancat respecte de la resta; en efecte, si el subtrahend és major que el minuend l’operació perd significat en l’àmbit dels nombres naturals. Aquesta propietat s’indica, amb símbols: a, b ∈ ℕ, a > b → a – b ∈ ℕ.

— No és tancat respecte de la divisió; en efecte, la relació de dos nombres naturals en general ja no és un nombre natural.

— És tancat respecte de la potenciació.

— No és tancat respecte de la radicació.

El problema del tancament d’un conjunt numèric respecte d’una operació ve de molt antic. En el cas de la subtracció, certament se’n va adonar la primera persona que es va trobar que havia de pagar més del que tenia i que, per a portar els comptes dels seus deutes, es va veure obligada a posar en pràctica molt abans que els matemàtics el concepte de nombre negatiu. De la mateixa manera que el primer cap de tribu que va haver de repartir fruites o un botí de caça entre la seva gent degué experimentar, sense adonar-se’n, el concepte de fracció. La tècnica emprada pels matemàtics per a resoldre aquest problema tan sols és més rigorosa i refinada, però substancialment és la mateixa. Cada vegada que han trobat operacions respecte de les quals els conjunts numèrics de què disposaven no eren tancats, els han ampliat introduint-hi nous elements per tal d’obtenir conjunts tancats respecte de l’operació que estaven estudiant. Fent aquestes ampliacions s’han atès a una regla important i sàvia, segons la qual quan s’amplia un conjunt cal que: a) el primer conjunt quedi contingut en el nou i b) les velles operacions es redefineixin en el nou conjunt de tal manera que les seves propietats no canviïn quan ens limitem a operar en el subconjunt dels vells elements.

D’aquesta manera, per a tenir un conjunt numèric tancat respecte de la diferència s’han inventat els nombres negatius.

Ampliant el conjunt dels nombres naturals amb l’afegit dels nombres negatius s’obté el conjunt dels nombres enters (que també es poden anomenar enters relatius), que s’indica amb la lletra M, la inicial de la paraula Zahl (en alemany, ‘nombre’). El conjunt M és el conjunt més petit que conté J i que és tancat respecte de la diferència. Per a tenir un conjunt numèric tancat respecte de la divisió s’han inventat els nombres que representen relacions entre enters. Així, ampliant el conjunt M s’ha obtingut el conjunt dels nombres racionals, que s’indica amb la lletra N, inicial de quocient, que és el conjunt més petit que conté M i que és tancat respecte de la divisió.

Avançant en la recerca de conjunts cada vegada més extensos i tancats respecte a un nombre cada vegada més gran d’operacions s’ha obtingut el conjunt dels nombres reals, que s’indica amb O i que conté les arrels dels nombres naturals, però que segons la definició que hem donat no es pot considerar tancat respecte de l’operació radicació, i, finalment, el conjunt dels nombres complexos, representat per L, que és tancat respecte de totes les operacions que recull el quadre 83.6, “Símbols de les operacions fonamentals”.

La jerarquia de les operacions

Hem conegut diversos tipus de nombres i hem après a utilitzar les operacions per a obtenir-ne de nous. Però fins ara hem fet les operacions d’una en una: 3 + 2 = 5, 5 – 4 = 1. Què passarà si fem alhora més d’una operació? Si volem fer alhora sumes i restes obtindrem una expressió aritmètica, per exemple: 3 + 2 + 5 – 4. Per a trobar el resultat mirem de fer les operacions per ordre, d’esquerra a dreta: 3 + 2 fan 5; sumem 5 a 5 i en tenim 10, del qual restem 4, i el resultat final serà 6. Per tant, podem escriure: 3 + 2 + 5 – 4 = 6. Si féssim les operacions de dreta a esquerra també obtindríem el mateix resultat. En efecte, – 4 + 5 fa 1, que sumat a 2 dóna 3, i sumat a 3 dóna 6. És ben senzill. Ara provem-ho amb aquesta expressió: 3 + 2  3. De seguida veiem que no és tan senzill com abans. Si sumem 3 i 2 ens dóna 5, que multiplicat per 3 dóna 15. Però si ho fem a la inversa i multipliquem 3 per 2 ens surt 6, al qual hem de sumar 3, que dóna 9. Cal trobar alguna regla! Doncs bé, la regla per a resoldre les expressions que contenen més d’una operació diu que, quan hi ha sumes, restes, multiplicacions i divisions, primer cal fer les multiplicacions i les divisions d’esquerra a dreta, i després les sumes i les restes, seguint l’ordre d’esquerra a dreta. D’altra banda, la suma i multiplicació solen anomenar-se operacions directes, mentre que la resta i la divisió s’identifiquen com a operacions inverses.

L'alfabet de la matemàtica: els nombres no enters

Hem dit abans que els matemàtics han anat inventant els conjunts numèrics a mesura que els anaven necessitant: ℤ, ℚ, ℝ, ℂ. Els nombres d’aquests conjunts també es representen, i aquesta és una altra part de l’alfabet de les matemàtiques.

Hi ha poca cosa a dir quant al conjunt dels enters ℤ, ja que es poden representar en qualsevol base, anteposant simplement el signe “–” al nombre si és negatiu.

En canvi, pel que fa als conjunts ℚ, ℝ i ℂ les coses no són tan fàcils.

Els nombres racionals i la representació en fraccions

El conjunt dels nombres racionals, ℚ, es defineix com el conjunt de nombres que expressen les relacions entre enters; per tant, és natural pensar a representar aquests nombres en forma de fraccions.

Ara bé, mentre que cada fracció representa només un sol nombre, cada nombre pot ser representat per infinites fraccions diferents, però equivalents, de les quals només una és reduïda als termes mínims, és a dir que té per numerador i denominador dos nombres primers entre ells (recordem que el numerador és el primer terme d’una fracció, i indica quantes parts de la unitat referida al denominador, el segon terme de la fracció, s’han de considerar).

Si afegim que el numerador i el denominador de la fracció són nombres enters, i com a tals es poden escriure en bases diferents, com hem vist abans, comprendrem que per a un nombre racional podem tenir una infinitat d’escriptures fraccionàries diferents, tantes com vulguem. Però les escriptures fraccionàries no es presten gaire als algorismes, a l’execució de les operacions. S’utilitza més l’escriptura anomenada decimal (per entendre’ns, la que duu una coma).

Per a estudiar aquesta escriptura partim d’un nombre qualsevol, per exemple 128,9271. És constituït per: a) 128, que representa la part entera i que indica, doncs, quants enters conté; b) 9 271, que s’anomena la part decimal i que indica la part fraccionària, inferior a la unitat, continguda en el nombre; c) la coma, que marca la separació entre la part entera i la decimal.

La fracció reduïda als mínims termes que representa el mateix nombre és 1 289 271/10 000; és una fracció impròpia, perquè el seu numerador és més gran que el denominador, i si fem la divisió entre aquests dos nombres enters trobem com a quocient 128 i com a residu 9 271. És a dir:

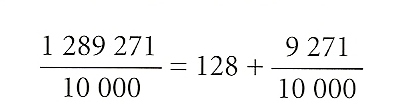
Aquesta operació de dividir el numerador pel denominador és a la base de l’escriptura decimal dels nombres racionals. En efecte, per a cada nombre racional es té:

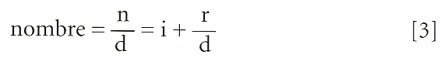
que també es pot escriure: nombre = n/d = i + r/d.

En la fórmula, n/d representa l’escriptura fraccionària del nombre; i + r/d és el punt de partida per a obtenir l’escriptura decimal: i és la part entera i r/d és la fracció pròpia l’escriptura decimal de la qual constituirà la part decimal. La paraula decimal indica que en aquesta escriptura figuren explícitament, al costat dels enters continguts en el nombre, les “dècimes”, com també, a més, les centèsimes, les mil·lèsimes... totes les quantitats que són representables com a inverses de les potències de 10.

Aleshores, es pot aplicar a l’escriptura decimal la fórmula [1], en la qual la part fraccionària es pot escriure utilitzant les potències d’exponent negatiu del número 10, entenent que 10–1 representa 1/10, 10–2 equival a 1/100, etc. En termes generals s’escriu que 10–h representa 1/10h, per a qualsevol h enter.

Així doncs, la fórmula que proporciona l’escriptura decimal d’un nombre és:

nombre = ck x 10k + ... + c1 x 101 + c0 x 100 + c–1 x 10–1 +

+ ... + c–h x 10–h [4]

Però en l’estudi de l’alfabet dels nombres s’ha vist que un enter es pot escriure en qualsevol base. I si provéssim d’escriure un nombre decimal en una base diferent de 10? No és difícil: només cal aplicar la fórmula [2] i completar-la amb les potències negatives del número n que s’ha elegit com a base. Aleshores es tindrà:

nombre = ck x nk + ... + c1 x n1 + c0 x n0 + c–1 x n–1 +

+ ... + c–h x n–h [5]

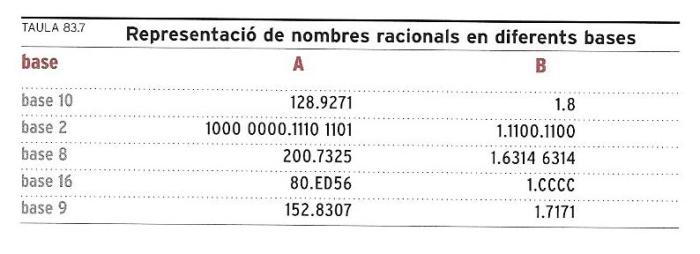
Quadre 83.7 Representació de nombres racionals en diferents bases.

ECSA

En el quadre 83.7, “Representació de nombres racionals en diferents bases”, s’exposen les escriptures dels nombres racionals 128,9271 i 1,8 tant en forma fraccionària com en forma decimal en algunes bases diferents. En aquest quadre, la part entera i la part decimal no estan separades per la coma, com és habitual en els nostres llibres, sinó per un punt. Aquesta és la pràctica anglosaxona, que cada cop s’imposa més, com en les calculadores, la “llengua materna” de les quals és l’anglès.

L’observació del quadre porta a fer algunes consideracions interessants. En primer lloc, cada nombre s’ha escrit en el quadre de cinc maneres diferents; és obvi que totes representen el mateix nombre, però com escollir-ne la més simple, la més fiable, la més universal? De fet, no hi ha una escriptura que sigui millor que les altres; segons el context i l’ús, segurament n’hi ha una de més oportuna, però depèn de cada cas. En els llibres apareix ara l’escriptura fraccionària, ara la decimal en base 10, mentre que en la memòria dels ordinadors més sovint es treballa amb les escriptures decimals en les bases 2, 8 o 16; la base 9, en canvi, només l’hem utilitzada per a jugar.

En segon lloc, observant el quadre es comprèn per què alguns autors opten per escriure el terme “decimal” entre cometes. En efecte, quan escrivim un nombre racional en una base diferent de 10, quin sentit té anomenar-lo ‘decimal’? Aquest terme té els seus orígens en la història de les matemàtiques, perquè aquest tipus d’escriptura va ser introduït pel matemàtic flamenc Simone Stevin el 1585. En aquella època ja s’emprava la notació posicional, però l’única base utilitzada era la base 10; aleshores el terme decimal permetia la distinció respecte dels enters. Per a tenir una teoria de la numeració d’altres bases cal esperar el segle XIX, i per a trobar-ne un ús habitual i estandarditzat ja ens acostem a èpoques molt recents, amb l’ús dels ordinadors, que han estès l’ús de nombres en diferents bases. Així, avui, per fixar una mica tots aquests conceptes, s’anomena decimal cadascuna de les xifres que formen la part no entera de l’expressió d’un nombre fraccionari.

Observem ara les escriptures decimals d’un mateix nombre en bases diferents. Es veu que el mateix nombre és periòdic en algunes bases, i en d’altres no. La fracció periòdica és l’expressió decimal que conté el període, o sigui, la xifra o el grup de xifres que es repeteixen indefinidament; per exemple, el període de la fracció 1/6 = 0,16666... és 6 (l’1, que indica les dècimes, s’anomena anteperíode).

L’explicació d’aquest fet es troba reflexionant sobre la fórmula [5]. La part decimal del nombre que descriu conté solament les potències negatives del nombre elegit com a base i és formada per un nombre finit de xifres només si representa una fracció que tingui com a denominador una potència de la base.

La periodicitat de l’escriptura decimal d’un nombre racional en una certa base està vinculada a la relació entre els factors primers d’aquesta i els factors primers del denominador de la fracció reduïda als mínims termes que el representa. En efecte: a) no és periòdica si la base conté tots els factors primers d’aquest denominador; b) és periòdica sense anteperíode si la base és un nombre primer amb aquest denominador; c) és periòdica amb anteperíode si la base conté alguns factors primers del denominador, però no tots.

Entreteniments decimals

A l’escola s’aprenen moltíssimes coses sobre els factors primers, sobre els nombres periòdics i sobre les seves fraccions generadores, tot en base decimal.

Concretament s’aprèn una regla que diu: “La fracció generadora d’un nombre periòdic és la fracció que té per numerador la diferència entre el nombre donat (escrit sense la coma i amb el període anotat una sola vegada) i el nombre format per totes les xifres que precedeixen el període, i per denominador el nombre format per tants 9 com xifres tingui el període, seguits per tants zeros com xifres tingui l’anteperíode.”

Què passaria si comencem a escriure els nombres decimals en altres bases? Podria ser un joc interessant per a nois espavilats. Com que no és fàcil reconstruir les escriptures decimals dels nombres en base diferent de la decimal convé treballar amb una calculadora, encara que sigui una de senzilla, que permeti escriure els nombres en una base qualsevol. Amb l’ajut de la calculadora es pot agafar un nombre racional, escrit com a fracció en base decimal, escollir una altra base, traduir-lo a una fracció d’aquella base i després fer-ne la divisió. Així es veu que la regla il·lustrada en la fórmula [3] val per a qualsevol base.

Però, i viceversa? Quina serà la regla per a reconstruir la fracció generadora en una base diferent de 10? Aquest pot ser un joc entretingut per a aspirants a matemàtics.

Els nombres reals

Quadre 83.8 Nombres i operacions.

ECSA

Al quadre 83.8, “Nombres i operacions”, es pot veure que el conjunt dels nombres reals és constituït pels racionals més els irracionals i els transcendents.

Com s’escriuen els nombres irracionals i els transcendents?

En general no s’expressen explícitament en forma d’alineacions decimals; es prefereix mantenir la indicació del que són: ZX2, 5ZX7, 3ZX–1, etc., o bé π, que a tot arreu representa la relació entre la longitud de la circumferència i el seu diàmetre. Però, com passa amb els nombres racionals, aquestes escriptures no es presten a l’execució de les operacions, per a les quals es prefereix generalment una escriptura en forma d’alineació de xifres del tipus de l’escriptura decimal dels racionals.

El problema és que ni els irracionals ni els nombres transcendents no poden ser representats per alineaments decimals finits, o periòdics. En els llibres es poden trobar expressions de π amb mil xifres decimals; hi ha programes sofisticats que visualitzen a la calculadora alineacions de centenars de xifres que representen nombres irracionals, però cap d’aquestes alineacions no “és” el nombre.

Això ho va descobrir Pitàgores a propòsit de ZX2. La descoberta el va deixar perplex i va posar en crisi la seva fe en la possibilitat de representar qualsevol quantitat mitjançant els nombres.

Més recentment, algú no entès en matemàtica també es pot sentir sorprès pel fet que no hi hagi cap fracció capaç de representar la relació entre la longitud de la circumferència i el seu diàmetre. En canvi, en l’àmbit de la ciència això no preocupa ningú, perquè se sap que les alineacions finites de xifres són representacions aproximades dels nombres irracionals i transcendents, se sap el valor de l’error que es comet utilitzant aquestes aproximacions, i un s’acontenta sabent quantes xifres s’han de fer servir perquè els errors comesos siguin negligibles.

La sintaxi de la matemàtica: les fórmules

En l’estudi d’una llengua, després d’aprendre’n l’alfabet, l’ortografia i la gramàtica, finalment s’és capaç de construir frases. Aleshores es passa a l’estudi de la sintaxi, que és el conjunt de les regles que permeten unir correctament les frases per a formar un discurs complet i articulat.

Pel que fa al llenguatge de les matemàtiques, hem parlat d’alfabet i d’ortografia a propòsit de l’escriptura dels nombres, i de gramàtica a propòsit de les operacions. El mot syntaxis, que en grec antic vol dir ‘disposició’, ‘ordre’ o ‘arranjament’ i també ‘alineació de batalla’, remet al conjunt de regles que permeten agrupar en una sola escriptura, anomenada fórmula, nombroses expressions numèriques diferents.

Lletres i nombres

Anteriorment hem vist cinc fórmules relacionades amb l’escriptura dels nombres. Ara, podríem reconsiderar-les i reflexionar una mica sobre què representen, com s’apliquen i com hem arribat a escriure-les.

Recordem per exemple la fórmula [1], que representa l’escriptura d’un nombre enter positiu qualsevol en base 10. Hi figuren nombres (10, 1, 0), símbols d’operació (“2” i “+”) i lletres (k, ck, ck–1, c1, c0).

El significat dels nombres i dels símbols d’operació és el mateix de què s’ha parlat en els paràgrafs anteriors. Però analitzem més atentament el significat de les lletres que hi figuren: k indica la longitud del nombre que volem escriure, és a dir, de quantes xifres consta; cadascuna de les lletres c representa una de les 10 xifres, i els subíndexs serveixen per a distingir les diverses lletres c, bé que continuen relacionades amb la corresponent potència de 10 a què es refereix cadascuna d’elles.

Per a aplicar la fórmula [1], en primer lloc cal establir quin valor enter positiu es donarà a k; consegüentment sabrem que el nombre que escriurem és format per k + 1 xifres, i que haurem d’assignar k + 1 valors a les lletres c corresponents. Un cop fetes aquestes assignacions i substituïdes en la fórmula [1] les lletres pels valors numèrics, la fórmula mateixa resultarà una expressió aritmètica. El seu resultat és un nombre determinat escrit en base 10. Assignant a k valors diferents s’obtenen nombres de longitud diferent; assignant a les c valors diferents s’obtenen nombres diferents. La fórmula [1], doncs, representa un nombre “qualsevol”. Per exemple, el número dos-cents cinquanta-sis (256) s’obté per a k= 2, c2 = 2, c1 = 5, c0 = 6; el número cinquanta-nou mil quaranta-nou (59 049) s’obté per a k = 4, c4 = 5, c3 = 9, c2 = 0, c1 = 4, c0 = 9.

La fórmula [1] l’havíem obtingut procedint al contrari del que hem fet fins ara per a explicar-la; efectivament, havíem partit de sis exemples de nombres escrits en base 10, que havíem agrupat al quadre 83.2, “Representació dels nombres en base 10”; després, analitzant aquests exemples, havíem obtingut la regla general per a l’escriptura d’un nombre en base 10; i finalment havíem buscat els símbols adequats per a escriure la regla de tal manera que anés bé per a representar qualsevol nombre.

Si tornem a seguir tots els passos ens adonem que al voltant d’aquella fórmula es poden distingir dos procediments: l’un ens ha portat d’alguns exemples puntuals a la formulació de la regla general, representada per la fórmula [1]; l’altre, de l’escriptura de la fórmula [1] ens mena a deduir com a casos concrets les escriptures de qualsevol nombre.

Es podria dir que el primer procediment és característic del treball dels matemàtics, dels qui busquen les regles i pensen les fórmules; i que el segon és característic dels usuaris de les matemàtiques, això és, dels qui apliquen les fórmules.

Si considerem la fórmula [2], ens adonarem que hi figuren menys nombres i més lletres que en la fórmula [1]. En efecte, en lloc del número10 figura cada vegada la lletra n, que és un enter positiu qualsevol i representa la base que volem escollir per a representar els nombres. La fórmula [2] és, doncs, més general que la fórmula [1], la qual hi és inclosa. Només cal posar n = 10 en la fórmula [2] per a tenir exactament la fórmula [1].

La substitució dels nombres per les lletres obeeix a una generalització, i a un camp més ampli d’aplicabilitat de les fórmules. Entre les lletres, com entre els nombres, també s’han de poder fer operacions: aleshores ens endinsem en el capítol de les matemàtiques que a escola s’estudia amb el nom de “càlcul literal”, i que proporciona les regles per a elaborar correctament les fórmules.

Els símbols matemàtics

El llenguatge de les matemàtiques utilitza moltíssim els símbols. Hem vist ja els símbols de les operacions fonamentals, i a “Lletres i nombres” hem considerat que les lletres poden utilitzar-se com a símbols per a indicar nombres. Com més evolucionen les matemàtiques, més aconsegueixen representar de manera general i sintètica expressions complicades, i més símbols hi incorporen.

La difusió dels esforços en aquest sentit és relativament recent; sobretot en aquest darrer segle, en què la facilitat de les comunicacions i els viatges han “empetitit” el món i han afavorit l’acostament de la gent i dels científics en particular, se sent la necessitat d’intercanviar informació sobre les pròpies recerques, de comunicar-se els resultats aconseguits, de realitzar un treball conjunt d’investigació a escala mundial. És important, doncs, posseir un llenguatge comú, que permeti comprendre’s sense gaires dificultats.

Com que les matemàtiques són un instrument que s’utilitza en quasi totes les branques de la ciència, és particularment important que els seus símbols siguin internacionals. Les fórmules matemàtiques, en efecte, són iguals en totes les llengües, com hem vist al començament d’aquest article. En canvi, les paraules que tradueixen aquests símbols a les diferents llengües no són internacionals; per exemple, el símbol Ö en català es llegeix ‘arrel quadrada’; en castellà, raíz cuadrada; en anglès, square root; i en francès, racine carrée. Així, resulta comprensible que els matemàtics s’entenguin més fàcilment per escrit que parlant.

De les lleis als models

En el punt anterior hem vist que les matemàtiques són un llenguatge, del qual hem estudiat una petita part, alguns signes alfabètics, algunes “paraules” i algunes regles de “gramàtica” i de “sintaxi”, tal com es podria fer amb una llengua qualsevol. Quan es coneix una mica una llengua, es pot començar a parlar-la, perquè és un instrument de comunicació que ens permet expressar conceptes, sentiments, raonaments, estats d’ànim, etc., de tal manera que els altres parlants de la llengua ens poden entendre i, si escau, respondre’ns.

De tot allò exposat en l’apartat anterior es desprèn que el llenguatge de les matemàtiques també serveix per a comunicar, i hem vist que és internacional, fins i tot més internacional que els alfabets; però què podem comunicar amb aquest llenguatge? De què serveix i per què és tan important?

Una antiga resposta a aquesta pregunta és la que va donar Galileu (1564-1642), el científic florentí, quan afirmà que “el gran llibre de la natura és escrit en llenguatge matemàtic”.

Galileu és considerat el fundador de la ciència “moderna”, perquè va insistir a fer una distinció entre la filosofia, que es pregunta per què passen les coses, i la ciència, que es pregunta com passen. Per tant, segons Galileu, el llenguatge de la matemàtica serveix per a descriure “com passen” els fenòmens de la natura. Val la pena entretenir-nos una mica a reflexionar-hi. Considerem un fenomen natural, per exemple, per no allunyar-nos d’un tema molt tractat per Galileu, la caiguda d’un objecte (que en física s’anomena un cos pesant).

Aquest fenomen es pot descriure de diferents maneres. Així, es pot dir: a) un cos abandonat a ell mateix cau fins que troba un obstacle que en frena la caiguda; b) un cos pesant lliure cau, i va guanyant velocitat a mesura que va caient; c) un cos pesant lliure cau a una velocitat proporcional al temps transcorregut des del començament de la caiguda.

Cadascuna d’aquestes frases descriu, en llengua catalana, la caiguda d’un cos, però les tres frases no són anàlogues. La primera expressa una observació qualitativa, poc detallada i que generalment es dóna en la natura; en efecte, llevat que el cos en qüestió pertanyi a un ocell que de sobte decideixi tornar a obrir les ales i deixar de caure o sigui algun objecte molt especial, com per exemple un globus aerostàtic, un cos, abandonat a ell mateix, cau. Aquesta frase no conté cap observació de tipus quantitatiu, que faci referència a la possibilitat de mesurar alguna cosa a propòsit de la caiguda.

La segona frase és més detallada; fa referència a una magnitud física, la velocitat de caiguda, de la qual dóna una descripció quantitativa molt elemental. Com que és una frase més precisa que l’anterior, descriu millor el fenomen de la caiguda, però també admet més excepcions; per exemple, si bé és cert que un paracaigudista cauria fins que un obstacle no el deturés, la seva velocitat de caiguda pot patir una reducció brusca quan obre el paracaigudes (i interromp així la caiguda lliure).

Ni la primera frase ni la segona no es poden traduir al llenguatge matemàtic de les fórmules que hem vist en el punt anterior. La tercera frase, en canvi, expressa una relació quantitativa precisa entre dues magnituds físiques que intervenen en el fenomen: la velocitat de caiguda i el temps transcorregut des del començament d’aquesta. Aquesta frase equival a la fórmula:

v = k t [6]

en què v representa la velocitat de caiguda al cap d’un temps t des que el cos ha començat a caure i k és una constant.

Quan Galileu deia que “el gran llibre de la natura és escrit en llenguatge matemàtic” volia dir que en tot fenomen natural intervenen magnituds que es poden mesurar, i que les relacions entre les seves mesures sempre es poden representar mitjançant fórmules matemàtiques.

Aquestes fórmules constitueixen la descripció de com s’esdevé el fenomen, i en el passat s’anomenaven també lleis del fenomen. Avui, el terme llei no agrada gaire, perquè suggereix la idea d’alguna cosa rigorosa, inderogable i, sobretot, sempre certa; en realitat, els fenòmens naturals s’esdevenen de manera molt menys precisa i regular que en la representació que en fan les lleis matemàtiques, que intenten objectivar-los i concretar-los de manera unívoca i universal.

Tornem a l’exemple de la caiguda d’un cos pesant. La fórmula escrita més amunt proporciona resultats clars, inequívocs, val per a qualsevol cos en caiguda lliure i permet saber la velocitat de caiguda fins i tot sense posar en pràctica l’experiment i sense fer cap mesurament instrumental. Aquests són els seus punts forts. Però també presenta punts dèbils, ja que no té en compte la resistència de l’aire que frena la caiguda, ni l’efecte dinàmic del vent, ni altres elements que, bé que en menor proporció, influeixen en la velocitat de caiguda. En essència, la fórmula descriu “bé” la caiguda d’un cos en el buit, però descriu “malament” la situació real d’un cos que cau sobre la Terra. (Els termes “bé” i “malament” també serien discutibles, i caldria posar-se d’acord sobre què volen dir realment en aquest context.)

En el llenguatge científic modern, doncs, es prefereix parlar de models més que no pas de lleis, i dir que el llenguatge matemàtic és el llenguatge més senzill capaç de proporcionar models eficients per a estudiar el comportament de la natura.

Els models matemàtics

La paraula ‘model’ era familiar en els temps en què la roba era de confecció artesana: el client triava el model del vestit, el sastre li prenia les mides i després feia el patró o model de paper, que necessitava per a tallar la tela. De vegades, per a alguns vestits particularment complicats i importants, feia un model intermedi en tela fina perquè el client se l’emprovés i poder-hi fer les modificacions i els retocs adequats abans de passar a l’operació irreversible de tallar la tela.

En totes aquestes operacions, el terme model s’ha utilitzat tres vegades, per a indicar tres coses diferents: primer, el tipus de vestit, el dissenyat per al maniquí; després, la plasmació en paper de les parts soltes; i en acabat, el muntatge de prova en tela del vestit sencer.

Tots tres significats contenen la idea comuna de model com a mostra, com a punt de referència per a arribar a la confecció d’un vestit tan semblant com sigui possible al que ha triat el client i que es correspongui al màxim amb la seva talla.

En el llenguatge actual, la paraula model és molt emprada, i en contextos diferents; per exemple, en l’àmbit artístic, es fa servir per a indicar tant l’objecte que l’artista es posa al davant a fi de reproduir-lo en proporcions iguals o diferents com la persona que posa en els estudis de pintors, escultors o fotògrafs (un o una model fotogràfics, per exemple); en el món de la moda, indica un nou tipus de vestit o de peça, del qual sovint es fa un nombre limitat d’exemplars (una desfilada de models, per exemple); en ètica, es parla de models per a referir-se a persones o coses que poden servir d’exemple (els models de virtut, dignes d’imitar, o els models negatius, que són objecte d’estudi dels sociòlegs i els psicòlegs); a més de molts altres àmbits on la paraula model indica un patró original, el prototip a partir del qual fer les còpies o, simplement, una representació simplificada de la realitat.

De tota manera, la idea comuna a tots els casos és la d’un referent al qual un pot remetre’s a l’hora de fer alguna cosa, sia un vestit o una obra d’art, un cotxe o una bona acció; el que en sortirà es podrà assemblar més o menys al model, però no serà idèntic a ell.

Quan parlem de models matemàtics també volem dir una cosa semblant, ja que estem pensant en un referent que expressa mitjançant fórmules matemàtiques el comportament ideal d’un fenomen. El mateix fenomen es dóna en la natura una, dues, cent, mil, deu mil vegades, però el fenomen real mai, o quasi mai, no és idèntic a l’ideal, tot i que sempre o quasi sempre s’hi assembla de manera satisfactòria. Analitzem aquestes consideracions més detalladament.

En primer lloc, un model matemàtic és una representació mitjançant fórmules, en la qual intervenen quantitats que en general són mesures de magnituds. Segons la branca científica a què es refereixin aquestes magnituds es parlarà de models matemàtics de la ciència en qüestió. Així, per exemple, es parlarà de models matemàtics per a la física, la química, la biologia o l’economia. Tota ciència que es proposi mesurar les seves magnituds i representar-ne el comportament mitjançant fórmules utilitzarà models matemàtics.

En segon lloc, s’ha dit que el model matemàtic representa el comportament ideal del fenomen. La paraula ‘ideal’ s’utilitza aquí com a sinònim d’abstracte, i no vol dir en absolut perfecte, com de vegades s’ha pensat equivocadament.

En la construcció d’un model matemàtic es parteix de l’observació del fenomen que es vol estudiar, s’analitzen les magnituds que hi intervenen i, mitjançant un procés d’abstracció i de tria dels paràmetres que semblen més rellevants, s’arriba a l’elaboració de les fórmules que constitueixen el model, el qual ja no representa el fenomen real sinó una abstracció, i és en aquest sentit que es parla de fenomen ideal.

En realitat, la construcció d’un model és més complexa i es procedeix per aproximacions successives. Primer s’elabora una versió del model, i després s’aplica, és a dir, s’utilitza per a preveure les mesures de les magnituds. Els resultats així obtinguts es comparen amb les mesures reals preses, i d’aquesta comparació es deriven modificacions del model. El procediment continua fins que el model obtingut és prou precís per a la idea pensada. En aquest cas es parla de models de primera aproximació, que són els més grollers, i, després, de models de segona, tercera aproximació, etc., que són cada vegada més precisos, però també generalment més complexos. Com es pot observar, encara que es tracti de models matemàtics en comptes de vestits, tampoc no hi ha tanta diferència entre aquesta manera de procedir i la del sastre de què parlàvem al començament de “Els models matemàtics”.

Seria convenient reflexionar una mica sobre el significat de l’expressió utilitzada abans, quan dèiem que un model és prou precís per al propòsit que ha de servir. Els fenòmens en la realitat es repeteixen de manera anàloga, però no idèntica. Tornant a l’exemple d’un cos pesant, mirem de repetir diverses vegades el mateix experiment, com el de deixar caure un objecte i de mesurar amb un cronòmetre el temps de la caiguda. Si la mesura fos molt precisa podríem verificar fàcilment que el resultat és diferent en cada cas, perquè canvien tant les condicions inicials, és a dir, el punt exacte des del qual deixem caure l’objecte, com les condicions de l’aire a través del qual cau (una mica més càlid, una mica més fred, del tot calmat o bé amb cops de vent), i també les condicions en què efectuem la mesura (simultaneïtat entre l’inici de la caiguda i la posada en marxa del cronòmetre, entre la fi de la caiguda i l’aturada del cronòmetre, fiabilitat del funcionament d’aquest aparell, etc.).

Amb tot, aquests resultats no serien gaire diferents entre ells; per exemple, les mesures de deu temps de caiguda d’una esfera d’acer des de la mateixa finestra són molt més semblants entre elles que no pas les mesures dels temps de caiguda d’un tros de paper.

Per tant, s’entén fàcilment que és absurd pretendre que un model representi exactament la realitat, mentre que, d’altra banda, és raonable esperar que la representi satisfactòriament, en el sentit que les mesures teòriques proporcionades pel model s’acostin prou a les reals, obtingudes en el curs dels experiments. Així, la quantificació dels termes “satisfactòriament” i “prou properes” depèn de l’objectiu que l’investigador es proposi. En l’exemple habitual de la caiguda, el model que proporciona la fórmula anterior es refereix a la situació ideal de la caiguda d’un cos en el buit, situació òbviament abstracta respecte de la nostra realitat quotidiana. El model representa de manera satisfactòria la caiguda d’una esfera d’acer, sobre la qual l’efecte de l’aire és negligible, però no representa gens bé la caiguda d’un tros de paper, i encara pitjor d’un globus, objectes que es ressenten de manera determinant de l’efecte de l’aire.

S’ha dit que quan un model no és prou precís per al propòsit que l’investigador persegueix, cal refinar-lo amb aproximacions successives; generalment, aquesta operació comporta la introducció de noves variables com, per exemple, en el cas de la caiguda, la resistència de l’aire, i per tant implica una complicació del model.

Normalment, doncs, com més complet és un model, més complicat i difícil és de gestionar. A més, com més fet a mida sigui per a descriure amb precisió un determinat fenomen, menor és el nombre de fenòmens a què s’adapta. És una mica el mateix que passa amb els vestits, atès que un model de línies folgades s’adapta a moltes més persones que no pas un vestit ajustat, les possibles imprecisions de tall i costura es noten menys i, per tant, es presta molt més a la fabricació en sèrie; d’altra banda, un vestit ajustat pot remarcar més la figura del qui el porta, de manera que, si això és el que es pretén, de vegades pot ser preferible, encara que pugui ser una mica més car.

En matemàtiques, des del moment que els models descriuen quantitats, seria raonable que el qualificatiu ‘precís’ referit a un model també fos quantificable, és a dir, expressable mitjançant nombres. Caldria trobar la manera d’expressar matemàticament l’error, la diferència entre les quantitats que s’obtenen a partir del model i les que es llegirien als instruments en fer l’experiment. Aleshores es plantejaria el problema de la construcció de models matemàtics per a la valoració dels errors. Aquest problema és complex, i no sempre es pot resoldre de manera satisfactòria. Per a determinats tipus de models, com els deterministes i els estàtics, existeixen criteris per a l’avaluació dels errors, però per a altres tipus de models de la moderna matemàtica encara no n’hi ha de prou fiables.

Però, ara, algú podria preguntar-se: si les matemàtiques només proporcionen models, on és realment la “veritat” matemàtica? Què és aleshores la tan esbombada “exactitud” de les matemàtiques? Albert Einstein, el creador d’un dels models més revolucionaris de la física contemporània, dóna a aquesta pregunta la resposta següent: “En la mesura en què les proposicions de les matemàtiques es refereixen a la realitat no són certes, i en la mesura en què són certes no es refereixen a la realitat. Només s’ha pogut arribar a l’aclariment perfecte d’aquesta qüestió gràcies a la tendència que en matemàtiques es coneix amb el nom d’axiomàtica. El progrés assolit per aquesta rau en el fet que la part lògica i formal és acuradament separada del contingut objectiu o intuïtiu”.

En altres paraules, les matemàtiques són “exactes” mentre operin dins els límits del pensament pur, mentre fixin els axiomes i les regles de raonament amb què construeixen estructures i dedueixen propietats que són fonamentals per a la construcció dels models; quan surten dels seus confins i s’apliquen a la natura, s’endinsen en la incertesa general de la realitat que les envolta. Aquesta conclusió, bé que sembla contradir l’afirmació de Galileu segons la qual la matemàtica és el llenguatge de la natura, no és al capdavall tan estranya. De la mateixa manera que tota llengua té les seves regles i expressa conceptes i idees, la matemàtica també té les seves regles de raonament, que utilitza per a expressar models. A més, quan el llenguatge s’utilitza per a comunicar, i allò important passa a ser el contingut de la comunicació, ens enfrontem al problema de no ser compresos, perquè no hem aconseguit expressar bé la nostra idea o perquè els altres no estan en la disposició adequada per a entendre-la, o pel motiu que sigui. Passa el mateix quan, emprant un model matemàtic per a descriure un fenomen, ens trobem el problema que la descripció matemàtica potser no es correspon amb la realitat. La descripció mai no aconsegueix ser perfecta, perquè el model no és prou precís, o perquè el fenomen és massa variable, o perquè les magnituds que hi intervenen no són prou identificables, o per qualsevol altre motiu. Com passa amb els altres llenguatges, en el cas del matemàtic, quan una descripció no és prou exacta es perfecciona amb més precisions, fins a arribar a una expressió satisfactòria.

Fins ara ens hem preocupat d’aclarir què és un model matemàtic, què representa i com es representa; val la pena reflexionar una mica més encara sobre la seva utilitat i la seva utilització. Retornem un moment al significat del terme model entès com un patró original, el prototip o el calc a partir del qual fer les còpies. Els models matemàtics també serveixen per a això; en efecte, a partir del model matemàtic d’un fenomen natural es poden obtenir mitjançant operacions de càlcul les mesures de les magnituds que hi intervenen, sense fer materialment l’experiment i, per tant, sense haver de fer les mesures instrumentals corresponents. Així, per exemple, en el cas de la caiguda d’un objecte, podem calcular la velocitat d’impacte contra terra mesurant simplement el temps de caiguda. Amb un model més complet que el proporcionat per la fórmula [6], fins i tot es pot deduir la mateixa dada simplement sabent l’altura des de la qual ha caigut.

En general, doncs, els models matemàtics fan la funció de proporcionar dades sense haver de fer experiments. En aquest sentit, en certs camps es parla de dades teòriques, que són les proporcionades pels models, per tal de distingir-les de les dades experimentals obtingudes de les mesures directes. La manera d’utilitzar els models depèn tant del camp d’aplicació com del context en què treballa l’usuari.

Es pot dir que sempre que es vulguin fer previsions cal utilitzar models i no una altra cosa, i que si es tracta de previsions quantitatives els models utilitzats són matemàtics. Aquestes consideracions expliquen almenys en part per què, malgrat la dosi d’arbitrarietat i incertesa que tenen els models, s’utilitzen cada cop en més camps, no solament en els clàssics, com la mecànica i la física, sinó també en camps com l’economia, la biologia i la sociologia, que són prou nous per al llenguatge matemàtic. Les raons d’aquesta difusió creixent rauen tant en el fet que els models són l’instrument més adequat per a les anàlisis quantitatives —a les quals tendeixen totes les disciplines que aspiren a ser considerades ciències—, com en el fet que el llenguatge de les matemàtiques és el més internacional, el més precís, però també —un cop superades les dificultats d’aprenentatge— el més fàcil dels llenguatges coneguts fins ara, expressió que pot arribar a sorprendre algú, però que resulta ben certa quan s’hi té una mica de pràctica.

Models matemàtics pensats com un joc

El joc d'endevinar la “carta secreta” (que és explicat a bastament aquí) és un model matemàtic que es realitza tirant i recollint tres vegades, d'una manera determinada, 21 cartes, disposades en set files i tres columnes. Un model matemàtic es concreta amb una fórmula (o un conjunt de fórmules), que ofereix uns resultats d'acord amb el tractament a què se sotmeten unes dades aportades segons unes indicacions determinades.

ECSA

S’ha dit que la manera d’utilitzar els models matemàtics depèn tant del camp d’aplicació com del context en què opera l’usuari. Així, doncs, considerem en primer lloc l’àmbit del joc, i analitzem algun dels models matemàtics que, sense adonar-se’n, utilitzen habitualment els nois a l’hora de jugar. Un model matemàtic és constituït generalment per un conjunt de fórmules; però si en una fórmula s’introdueixen dades, per exemple assignant valors numèrics determinats a certes lletres que hi figuren, s’obtenen consegüentment resultats. Aleshores es pot dir que, més en general, un model matemàtic funciona com un giny capaç de respondre amb uns resultats a unes dades proporcionades des de fora.

Per exemple, si en la fórmula de la caiguda lliure v = k t s’assigna a k el valor de 9,80 m/s2 (que no és una dada triada a l’atzar, sinó que s’ha calculat experimentalment i que val per a tots els cossos que cauen a la Terra), i si s’assigna a t el valor de 10 s, s’obté com a resultat que la velocitat d’un cos al cap de deu segons de caiguda és igual a 98 m/s; si s’assigna a t el valor de 5 s s’obté com a resultat que un cos al cap de cinc segons de caiguda té una velocitat de 49 m/s, i així successivament.

Imaginem-nos ara dos nois que es posen junts a fer experiments sobre la velocitat de caiguda dels cossos, i imaginem-nos que un d’ells sap la fórmula i l’altre no. El que no sap res de física quedarà parat de la capacitat de l’altre de preveure el resultat de les diferents proves. Per tant, és pensable poder utilitzar els models matemàtics d’una manera gens científica per a fer-nos passar per màgics, un ús que certament era força freqüent a l’antiguitat, per exemple entre els membres de l’escola de Pitàgores. Als nostres dies, aquesta aplicació és habitual en els jocs infantils. Vegem ara alguns “jocs màgics” destinats als més petits, i retirem l’embolcall de la màgia per descobrir el model matemàtic que amaguen. Comencem pel joc que podríem anomenar “Sé quin número penses”. És un joc clàssic, prou conegut pels nens quan estan aprenent les quatre regles aritmètiques. Es fa entre dues persones (que anomenarem el mag i en Pere) i funciona així. El mag diu a en Pere: “pensa un número”, i en Pere pensa, per exemple, el número 3; després, el mag li diu: “multiplica’l per dos”, i en Pere pensa “6”; després, “suma-li 10”, i en Pere pensa “16”; “i, ara, divideix-lo per dos”, diu el mag, i a en Pere li surt el 8; aleshores: “resta-li el número que has pensat”, i en Pere pensa “5”; finalment, el mag exclama: “t’ha sortit el 5!”. El joc es pot repetir tantes vegades com es vulgui, i el mag sempre endevinarà el nombre que li ha sortit a en Pere.

Mentre en Pere és petit s’empassa sense més ni més la història de la màgia, però si ja és una mica gran començarà a rumiar i és probable que trobi la clau de la resposta: el nombre que li surt al final del joc sempre és la meitat del nombre que el mag li havia fet sumar. Per entendre bé com va la cosa, ara analitzarem pas a pas el model matemàtic d’aquest joc.

El mag matemàtic no sap quin nombre ha pensat en Pere, de manera que l’anomena x. Quan li demana que el dobli, al cap d’en Pere hi haurà un altre nombre, que el mag ignora, però que anomenarà 2x. Quan li demana que li sumi 10, en Pere forma el nombre 2x + 10. Quan li demana que el divideixi per dos (la qual cosa no és en absolut indispensable per al funcionament del joc, però és un pas que contribueix a confondre les idees), en Pere tindrà al cap el nombre x + 5. Si, per acabar, li demana que en resti el nombre que havia pensat al principi, en Pere obtindrà 5, que és precisament la meitat del nombre sumat a petició del mag. El truc consisteix, doncs, a utilitzar un model en què el resultat depengui solament de la dada proporcionada pel mag, i no del nombre que pensa en Pere.

Un altre joc d’aquest mateix estil és “L’endevinalla de la carta secreta”. Es tracta d’un joc de cartes molt distret, en què l’ús d’un model matemàtic es pot combinar al final amb un truc efectista d’agilitat manual, i en què també farem intervenir el mag i en Pere. El mag col·loca sobre la taula 21 cartes, cara amunt, repartides en set files de tres columnes (vegeu, a la figura, les columnes a, b i c del bloc de l’esquerra), i convida en Pere a triar-ne una, sense dir-la. En Pere tria la carta que li sembla (per exemple, la carta marcada amb el número 2) i assenyala al mag la columna en què hi ha la carta que acaba de triar (la columna b de la primera fila, en aquest exemple). El mag recull les 21 cartes d’una manera determinada i les torna a disposar damunt la taula, també destapades, en set files de tres columnes, com abans, i torna a demanar a en Pere a quina columna es troba ara la carta que havia triat en la primera operació (la carta número 2 és ara a la columna b de la tercera fila del bloc central). Després, torna a recollir les 21 cartes d’una manera determinada i, per tercera vegada, les disposa damunt la taula, destapades, en set files de tres columnes, i altre cop demana a en Pere a quina columna és la carta que havia triat abans (ara, la carta número 2 és a la columna a de la quarta fila del bloc de la dreta). Aleshores el mag recull només la columna de les set cartes on hi ha la carta secreta (la columna a, a l’exemple), agafa el pilonet de cartes lateralment, les ensenya a en Pere, en fa sobresortir subtilment i amb traça la carta central i, sorpresa!, la carta que s’insinua és precisament la carta secreta d’en Pere.

El model matemàtic d’aquest joc s’ordeix en les tres vegades que el mag disposa i recull les cartes. Tot el joc és pensat perquè la carta secreta d’en Pere acabi, després dels tres passos, precisament a la fila central de l’estesa de cartes. L’última part del joc, en canvi, és només d’agilitat manual per a aconseguir que del pilonet de les set cartes finals sobresurti la carta central.

La base de l’èxit d’aquest joc com a model matemàtic rau en el fet de disposar les cartes sobre la taula d’una manera determinada, com dèiem abans. Així, el mag tira les cartes sobre la taula, d’esquerra a dreta, en files de tres (horitzontalment) i les recull de dalt a baix (verticalment), tenint en compte sobretot que la columna que conté la carta secreta ha de ser recollida sempre en segon lloc. L’ordre de recollida de les altres dues columnes és indiferent. Per això, encara que el mag desconeix inicialment quina és la carta secreta, aquesta estratègia en la disposició i la recollida de les cartes li aporta dues informacions primordials: la primera, que la segona vegada que tiri les cartes sobre la taula la carta secreta serà entre la vuitena i la catorzena posició del conjunt (vegeu a la figura les set cartes ressaltades, de la 2 a la 20); i l’altra, com que ha recollit sempre en segon lloc la columna indicada, que la tercera vegada que disposi les cartes sobre la taula la carta secreta ocuparà el primer o el segon o tercer lloc de la fila central, i el mag sabrà exactament quina és quan en Pere li assenyali la columna en què diu que hi ha la carta que ha triat (a l’exemple, en assenyalar en Pere que la carta secreta és a la primera columna, el mag sap immediatament que es tracta de la carta 2 i en descarta l’11 i la 20 com a possibles).

L’últim joc que us proposem és l’anomenat “A quina distància és la tempesta?”. En aquest joc, no hi participen ni el mag ni en Pere i tampoc no és cap joc de màgia, sinó que es tracta de l’ús científic d’un model matemàtic, que permet establir la distància aproximada a què ha caigut un llamp durant una tempesta.

Es pot determinar aquesta distància simplement comptant amb un cronòmetre quants segons passen entre el moment en què es veu la resplendor del llampec i el moment en què se sent el tro corresponent, i multiplicant aquest nombre de segons per 340. D’aquesta manera s’obté la distància, mesurada en metres, entre el punt on ha caigut el llamp i nosaltres. En aquesta operació s’aplica un model matemàtic i, per bé que sigui un joc, es tracta, com hem dit, d’una aplicació científica, en què s’utilitzen el model i una dada obtinguda experimentalment (el nombre de segons) per a arribar a un resultat que és impossible mesurar directament.

En el fenomen físic, es produeix una descàrrega elèctrica (el llamp), que genera una gran lluentor (el llampec) i un estrèpit (el tro). Tots dos fenòmens tenen lloc simultàniament, però es propaguen a velocitats molt diferents: la llum del llampec es propaga rapidíssimament, fins al punt que es pot considerar que es veu just en el moment de la descàrrega, mentre que el so es propaga més lentament, a una velocitat gairebé constant d’uns 340 m/s. El soroll del tro arriba, doncs, a les nostres orelles amb retard respecte del llampec, retard que és més gran com més lluny s’hagi produït el fenomen.

El model matemàtic corresponent és donat, doncs, per la fórmula: e = k t, en què e és l’espai recorregut pel so, k és la seva velocitat i t és el temps de propagació; com que k = 340 m/s, si amb un cronòmetre mesurem t, és a dir, el nombre de segons que passen entre el llamp i el tro, obtindrem la distància buscada, e. És una mena de joc amb base científica divertit i útil. Serveix per a saber si els llamps estan caient a prop o lluny i, per tant, si cal buscar aixopluc sense dilació.

Però en aquest cas, com en el dels models científics més consistents, el model tampoc no ens proporciona un resultat exacte, perquè la velocitat del so no és del tot constant, l’aire no és del tot immòbil (sobretot durant les tempestes), el cronòmetre no és del tot precís, de la mateixa manera que els nostres reflexos a l’hora de posar-lo en marxa i parar-lo tampoc no són perfectes. Amb tot, el resultat que obtenim de l’experiment és acceptable, almenys per al context en què ha de servir.

Un joc semblant és el que podríem anomenar “La profunditat d’un precipici”. Consisteix a cronometrar el temps que triga una pedra a caure fins al fons d’un barranc (o un pou, o algun altre forat profund) i a determinar quants metres té de profunditat, simplement multiplicant per 4,9 el quadrat del nombre de segons trobat. El model matemàtic d’aquest fenomen, que és un refinament de la fórmula [6] sobre la caiguda dels cossos, pot ser expressat per la fórmula: e = 1/2 k t2, en què t és el nombre de segons de caiguda, k és la mateixa constant que figurava en la fórmula [6] amb un valor de 9,80 m/s2, i e és la profunditat expressada en metres.

El món segons els models geomètrics

Geometria, que en grec significa la ‘mesura de la Terra’, és un terme que ha passat a indicar la branca de les matemàtiques que estudia les propietats de l’espai que ens envolta i de les seves parts constituents, és a dir, que es dedica bàsicament a l’estudi de les figures geomètriques i a les propietats que es refereixen a la forma, extensió i estructura d’aquestes figures.

La geometria és, doncs, la part de les matemàtiques que proporciona els models per a descriure com és l’univers en què vivim; en canvi, no és adequada per a descriure com passen les coses. Parlem de models perquè les figures que estudia són figures ideals, abstractes, que utilitzem per a descriure els objectes reals amb una precisió que depèn de l’objectiu que ens hàgim fixat. Així, per exemple, quan diem que la Terra és una esfera que té un radi de 6 378 km, encabim la Terra en un model geomètric; en realitat, la Terra no és exactament una esfera, perquè la distància del seu centre a cadascun dels pols és menor que el radi de l’equador.

Però l’esfera de radi 6 378 km és un bon model, que permet descriure —amb dades i mesures prou precises— tant fenòmens que tenen lloc a una distància de centenars de quilòmetres com l’aparició o la desaparició d’un vaixell a l’horitzó, la posició i l’alçada d’un far a la costa, i també fenòmens que s’esdevenen molt lluny, com l’ombra de la Terra sobre la Lluna durant els eclipsis lunars.

Certament, l’esfera constitueix un model per a descriure la Terra molt millor que el pla, utilitzat per alguns filòsofs a l’antiguitat més remota. Amb tot, un model de Terra plana pot resultar satisfactori amb vista a descriure’n i mesurar-ne petites parts, contingudes en un radi de pocs quilòmetres. Quan parlem de planes o altiplans, quan diem que la superfície d’una bassa és plana, quan calculem les mides d’una plaça, d’un tros de terra o del terra de la cuina utilitzant les fórmules per al càlcul de les àrees de figures planes, utilitzem, sense adonar-nos-en, aquell model. I si algú mirés de retreure’ns-ho o de corregir-nos l’error, ens posaríem a riure i li diríem que va errat.

A propòsit dels models de la geometria, convé observar que es tracta de models matemàtics tant perquè interessen mesures de magnituds com àrees, longituds i volums, com perquè s’hi treballa segons un rigorós pla teòric i amb unes regles de raonament precises. En aquest sentit, és interessant remarcar que aquest pla teòric rigorós i aquestes regles de raonament van ser formulats per Euclides, un matemàtic grec que va viure pels volts del 300 aC. La geometria és, doncs, la més antiga de les disciplines matemàtiques, la que ha proporcionat a la ciència els primers models.

L’obra principal que va escriure són els Elements, en tretze volums, que van constituir amb quasi tota probabilitat el llibre de text de l’escola d’Alexandria, on ensenyava Euclides, una de les escoles més famoses i importants de l’antiguitat. Traduïts a totes les llengües i utilitzats durant dinou segles com a única geometria possible, encara avui són a la base de l’ensenyament de la geometria en moltes escoles.

Sense allunyar-nos encara de l’antiguitat, vegem què pensava Plató, un filòsof grec que va viure pels volts del 350 aC, a propòsit dels geòmetres i de la geometria: “Els geòmetres se serveixen de figures visibles, sobre les quals raonen, però no pensant en elles sinó en allò de què són la imatge, i raonen sobre el quadrat en si i sobre la diagonal en si, i no pas sobre el que dibuixen. El mateix es pot dir sobre totes les figures, que ells modelen i dibuixen, de les quals se serveixen com a imatges, bo i intentant veure-hi les veritables entitats que només es poden veure amb el pensament”.

Plató, doncs, ja era conscient del caràcter abstracte de les figures geomètriques; s’hauria pogut dir que ell també les considerava models. En realitat, a la base de la seva manera de pensar hi havia una concepció diferent de la nostra, perquè creia que aquestes figures existien de veritat i que el pensament humà les havia de descobrir i “veure”, mentre que nosaltres tendim a considerar-les abstraccions, meres creacions del pensament.

Vegem ara una última característica dels models geomètrics de què estem parlant, atès que poden descriure i mesurar les figures, les quals es relacionen mitjançant relacions d’equivalència. Així, per exemple, quan Arquimedes descobreix el volum de l’esfera, diu que “tot cilindre que tingui com a base el cercle màxim de l’esfera i una altura igual al diàmetre de l’esfera, té un volum que és una vegada i mitja el de l’esfera” (com es podria comprovar sabent que el volum d’un cilindre és Vc = π r2 h, i el volum d’una esfera és Ve = 4/3 π r3). Per tant, Arquimedes va establir la relació entre el volum d’una esfera i el d’un cilindre determinat, en què el coneixement de l’un ens permet obtenir el de l’altre.

Anàlogament, en estudiar geometria a escola, vam aprendre a calcular l’àrea del paral·lelepípede remetent-nos a la del rectangle, l’àrea del triangle remetent-nos a la del paral·lelepípede, el volum de la piràmide remetent-nos al del prisma, i així successivament.

Flatlàndia i Esferolàndia

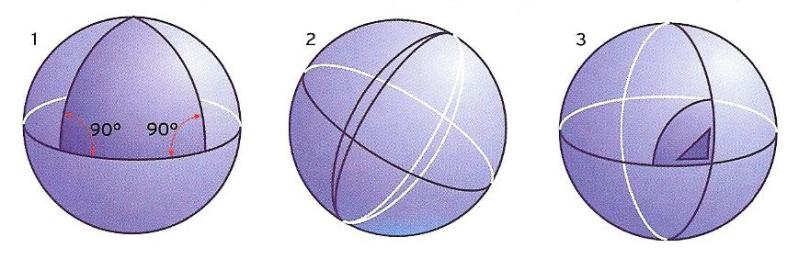
A Esferolàndia -un “país” regit per la geometria esfèrica (vegeu el text)- els costats d'un triangle són arcs de circumferència i els seus angles interns sumen més de 180°(figura 1); a més, les rectes són cercles i no n'hi ha de paral·leles (figura 2). Tot i això, les geometries bidimensional i esfèrica coincideixen si es consideren figures prou petites (figura 3).

ECSA

Per a mesurar una part petita de la superfície terrestre, n’hi ha prou amb un model pla de la Terra. Anomenarem aquest model Flatlàndia, terme tret del títol d’un llibre d’E.A. Abbot (1838-1926), anomenat Flatland, que descriu un món pla de dues dimensions (en anglès, flat significa ‘pla’ i land, ‘terra’). En un món com aquest, la geometria és l’euclidiana, tradicionalment ensenyada a les nostres escoles, és a dir, la geometria formalitzada per Euclides en els seus Elements, on es posen en relleu alguns termes fonamentals —punt, recta, pla—, que són enumerats amb una sèrie de definicions senzilles. Per exemple, el punt és “allò que no té parts”, la línia és “una longitud sense amplitud”, i així successivament. D’aquests termes s’enuncien les proposicions bàsiques, és a dir, els postulats.

Per exemple, el primer postulat d’Euclides afirma que per dos punts diferents passa una recta i només una; el segon ens diu que la recta es pot allargar indefinidament, és a dir que és una línia infinita i il·limitada; el cinquè, que per un punt extern a una recta pot passar només una sola paral·lela a la recta.

Com a conseqüència d’aquests postulats trobem, entre altres coses, que la mínima distància entre dos punts és el segment de recta que els uneix, o que la suma dels angles interns d’un triangle és 180°. Tot això és cert quant a la realitat propera a nosaltres, la que els nostres ulls poden percebre. En efecte, si haguéssim de desplaçar-nos d’un punt a un altre d’una plaça, triaríem de manera natural, per estalviar temps i esforços, el recorregut imaginari que uneix els dos llocs en línia recta; si pensem en les vies del tren, el cinquè postulat ens semblarà una veritat indiscutible; i no podríem pensar en absolut en un triangle amb dos angles rectes. En general, doncs, la geometria euclidiana descriu perfectament l’espai físic que ens envolta.

Imaginem-nos ara un mariner que navega pels mars de la Terra. Quin model geomètric descriurà millor l’espai físic pel qual es mou? És evident que el model que hem anomenat Flatlàndia no funciona, perquè la superfície de la Terra és aproximadament una superfície esfèrica; així doncs, anomenem Esferolàndia el nostre nou model i vegem quina geometria és vàlida per a descriure els fets experimentals en un món així. Els navegants de l’antiguitat ja sabien que sobre la superfície esfèrica el camí més curt entre dos punts donats és un arc de cercle màxim, és a dir, l’arc d’una circumferència obtinguda fent intersecar-se la superfície amb un pla que passa pel centre de l’esfera, i per a ells era natural considerar aquests arcs com a segments d’una geometria bidimensional especial, anomenada geometria esfèrica, que seria la geometria d’Esferolàndia.

Aquí les rectes són els cercles màxims; no són les línies infinites i il·limitades de Flatlàndia, sinó línies que, tot i ser il·limitades —en el sentit que poden ser recorregudes de manera contínua sense aturar-se mai—, tenen una longitud finita. A Esferolàndia, els costats dels triangles no són pròpiament segments, sinó arcs de circumferència; per això, la suma dels angles interns no és 180° sinó un nombre més alt de graus. Per tant, és possible tenir triangles amb dos angles rectes (figura 1). A més, com que les rectes són cercles màxims, dues rectes qualssevol es troben sempre en dos punts de la superfície esfèrica diametralment oposats; consegüentment, no hi ha rectes paral·leles (figura 2).

És natural preguntar-se si les geometries de Flatlàndia i Esferolàndia són totalment diferents, és a dir, si parteixen de postulats totalment diferents, o si alguns dels postulats de la geometria euclidiana continuen essent vàlids en la geometria esfèrica. Examinem el primer postulat d’Euclides: “Per dos punts només passa una recta”. Aparentment, això no és vàlid en la superfície esfèrica, perquè pels pols passen infinits cercles màxims, és a dir, infinites rectes. Però si es defineixen com a punts antipodals dos punts diametralment oposats en la superfície esfèrica, el primer postulat encara és vàlid, enunciat així: “Per dos punts no antipodals només passa una recta”. En canvi, ja no és vàlid el segon postulat, perquè cau la infinitud de la recta, i tampoc no ho és el cinquè, perquè a Esferolàndia no existeixen rectes paral·leles. En canvi, tots els altres postulats mantenen la seva validesa.

Així, quina geometria és la bona, la de Flatlàndia o la d’Esferolàndia? Aquesta és una pregunta sense resposta, perquè les geometries només són llenguatges, que poden expressar de manera més o menys adequada certes estructures d’objectes. Per això és més correcte parlar d’adequació, funcionalitat i comoditat d’una geometria més que no pas de veritat.

De fet, també es comprova que, si la part de superfície esfèrica és prou petita, les dues geometries coincideixen. En efecte, un arc de circumferència prou petit es pot comparar amb un segment, i els triangles petits d’Esferolàndia coincideixen amb els de Flatlàndia (figura 3). De totes maneres, en general, en canviar de model també canvia la geometria. En una pel·lícula de fa uns anys, el protagonista, Sherlock Holmes, aleshores un estudiant d’institut, plantejava al jove Watson, també estudiant, la pregunta següent: “Un home, després de caminar durant 10 milles recte cap endavant en direcció al sud, gira 90° cap a l’est, avança10 milles més, gira 90° cap al nord i, després de recórrer 10 milles més, arriba al punt d’on havia sortit, on troba un ós. De quin color és l’ós?”.

El pobre Watson, sòlidament ancorat en la geometria euclidiana, no sabia contestar, però si hagués canviat de model, quina resposta hauria donat? (La resposta a la pregunta es troba just a la fotografia del costat.)

Quina forma té l'univers?

Els éssers humans, des dels temps més reculats, s’han preguntat en observar el cel quina forma té l’univers, és a dir, quina és l’estructura de l’espai on són la Terra, el Sol i els estels.

Els primers astrònoms veien moure’s els astres per la volta celeste com per una superfície esfèrica, per la qual alguns cossos, anomenats estels fixos, giraven amb regularitat d’est a oest; per tant, era natural postular que l’univers era finit. Aristòtil, per exemple, pensava que no hi podia haver espai més enllà de l’esfera dels estels fixos, i afirmava: “Més enllà del cel no hi pot haver ni posició ni buit ni temps”. Però amb la difusió de les teories geomètriques expressades per Euclides en els seus Elements, es va atribuir a l’univers una estructura geomètrica de tipus euclidià, i l’espai es va concebre infinitament extens. Com que durant molts segles la geometria euclidiana es va considerar l’única veritable i possible, es va consolidar aquesta teoria de la infinitud de l’espai. Galileu, en considerar la geometria euclidiana, escrivia que “els triangles, els cercles i altres figures ens ensenyen la llengua matemàtica en què s’ha escrit aquest immens llibre, vull dir l’univers, que mai no deixa d’estar obert als nostres ulls”. La física newtoniana també va contribuir a reforçar el “sentit comú euclidià”, fins que, a la primera meitat del segle XIX, es van desenvolupar les geometries no euclidianes. Va ser el matemàtic alemany Bernhard Riemann qui va tenir la idea que la geometria de la superfície esfèrica, la d’Esferolàndia, per entendre’ns, podia aplicar-se a tres dimensions, o potser a més de tres. De la mateixa manera que una línia pot ser finita però il·limitada, el caràcter il·limitat de l’espai no implica necessàriament que tingui un volum infinit. Es pot pensar perfectament en l’existència d’un telescopi prou potent que facilités a un astrònom la visió del que hi ha a la seva esquena, deixant de banda el petit detall que la llum trigaria milers de milions d’anys a recórrer la distància des de l’esquena fins a l’ull que l’observa. En un espai corbat com aquest, les rectes que uneixen dos punts són les corbes de mínima longitud entre tots dos punts.

Aquesta idea, que l’espai pot ser il·limitat sense ser infinit, va ser represa més tard per Einstein en la seva teoria de la relativitat general. En aquesta teoria, l’espai ja no és tridimensional, sinó de quatre dimensions, atès que la posició d’un punt és determinada per les tres coordenades espacials més una de temporal. La geometria vàlida en un espai així no és l’euclidiana sinó la de Riemann, en què la llum es propaga al llarg de les corbes de longitud mínima (geodèsiques) i la curvatura de l’espai és determinada per la matèria que l’omple. Així, doncs, per a Einstein l’univers és corbat i finit, amb una forma que depèn de la matèria que conté, i, sorprenentment, de quatre dimensions.

Les dimensions de l'espai

La construcció de la corba de Von Koch representa l'acoblament en fases successives d'una sèrie repetitiva de figures. Constitueix una explicació bàsica de les fractals, un exemple “natural” de les quals són les disposicions “regularment capricioses” d'un cristall de glaç.

ECSA

Hem vist que la teoria de la relativitat indueix a prendre en consideració un espai quadridimensional. Indubtablement, condicionats com estem per les tres dimensions de la nostra experiència quotidiana, cal un cert esforç d’imaginació per a representar-nos mentalment un espai d’aquesta mena, i ens és molt difícil pensar en mons de dimensions diferents que el nostre, ja que ens veiem obligats a buscar i a establir nous punts de referència generals.

En el llibre ja esmentat d’E.A. Abbot s’il·lustren mons de diferents dimensions. El més elemental d’aquests universos és Linelàndia, un món d’una dimensió, del qual el Quadrat, el protagonista del llibre, fa la descripció següent: “Em vaig veure davant una vasta multitud de petits segments de recta, barrejats amb altres éssers encara més petits, amb una naturalesa de punts lluminosos, que es movien tots endavant i endarrere al llarg d’una sola Línia Recta... En acostar-me a un segment més gran, el vaig interpel·lar, però no em va contestar. Com que vaig perdre la paciència davant del que em semblava una mala educació intolerable, vaig repetir la meva pregunta en veu alta”. Aleshores el segment interpel·lat pel Quadrat es digna a respondre i declara que és el rei del món, el monarca de Linelàndia.

“Semblava que aquest pobre i ignorant monarca, com ell mateix s’anomenava, estigués convençut que la Línia Recta, que ell anomenava el seu reialme, i on menava la seva existència, constituís el món sencer, tot l’espai. Com que no es podia moure ni veure res més que la seva Línia Recta, no concebia res més fora d’ella... Els súbdits, dels quals els petits segments eren els homes i els punts les dones, eren tots igualment confinats, quant al moviment i la visió, a l’única Línia Recta, que era tot el seu món. No cal afegir que tot el seu horitzó es limitava a un punt, i que ningú no podia veure res tret d’un punt.”

Cap dels habitants de Linelàndia no s’imagina que pugui existir un món diferent d’aquell on viuen, i quan el Quadrat intenta explicar al rei què és la segona dimensió, no solament no el creuen, sinó que fins i tot el fan fora furiosament.

En canvi, el món bidimensional, Flatlàndia, és més complex i articulat. El Quadrat, que hi viu, en parla així: “Imagineu-vos un gran full de paper pel qual Línies Rectes, Triangles, Quadrats, Pentàgons, Hexàgons i altres figures geomètriques, en comptes d’estar-se quietes, es mouen d’ací d’allà, lliurement, per la superfície o per l’interior d’aquesta, però sense poder-se’n separar i sense poder-s’hi submergir. En una paraula, com ombres, però consistents, i amb els contorns lluminosos. Així tindreu una idea força correcta del meu país i dels meus compatriotes”.

Els habitants de Flatlàndia també estan dividits segons una rígida jerarquia social.

“Les nostres dones són segments de Línies Rectes. Els nostres soldats i els obrers de les classes inferiors són Triangles Isòsceles. La nostra burgesia és formada per Equilàters, o triangles amb els costats iguals. Els nostres professionals i nobles són els Quadrats i els Pentàgons. Immediatament per sobre d’aquests hi ha l’aristocràcia, dividida en diversos graus, començant per les Figures de Sis Costats, o Hexàgons, després dels quals hi ha les figures de més costats, fins que arribem al títol de Poligonals, que són les que tenen molts costats. Per acabar, quan el nombre de costats esdevé tan gran, i els costats tan petits que la figura ja es confon amb un cercle, s’entra a formar part de l’Orde Circular o Sacerdotal; i aquesta és la classe més privilegiada de totes.”

En un país així, tot el que els habitants veuen els uns dels altres, quan es troben, són segments, més llargs quan els éssers són a prop i més curts quan són lluny. Es distingeixen els uns dels altres per una lluminositat que cadascú posseeix i que és més accentuada com més gran és la importància del personatge.

En un moment donat, la vida tranquil·la del Quadrat protagonista es veu sacsejada per l’aparició d’un ésser extraordinari, que es presenta com a Esfera, i declara que procedeix de la tercera dimensió. El Quadrat, incrèdul, no pot concebre un món així, i discuteix llargament amb el nouvingut, el qual no pot fer altra cosa, per a convèncer l’escèptic, que portar-lo al seu món de tres dimensions, Espaciolàndia. El Quadrat és traslladat a l’espai i des de dalt veu casa seva i tots els detalls que fins aleshores només havia pogut copsar mitjançant la raó.

“Em vaig sentir elevat a l’Espai. Era exactament com m’havia dit l’Esfera. Com més ens allunyàvem de l’objecte que estàvem observant, més augmentava el camp visual. La meva ciutat, amb l’interior de cada casa i de totes les criatures que contenien, s’oferia a la meva mirada com en miniatura. Vam pujar encara més i, oh!, els secrets de la terra, les profunditats de les mines i les cavernes més remotes de les muntanyes, tot es desplegava al meu davant.”

A Espaciolàndia, el Quadrat descobreix les figures sòlides i coneix un Cub. “I aleshores em va presentar el Cub, i vaig descobrir que aquest Ésser meravellós en realitat no era un Pla sinó un Sòlid; i que era dotat de sis cares planes i de vuit punts terminals anomenats angles sòlids. Vaig recordar l’afirmació de l’Esfera, que precisament una criatura com aquesta seria formada per un Quadrat que es mogués per l’Espai paral·lelament a ell mateix; i em va plaure la idea que una criatura tan insignificant com jo era pogués ser considerada en un cert sentit la Progenitora d’un fill tan il·lustre.”

Aleshores el curiós Quadrat, al qual s’han revelat els misteris d’Espaciolàndia, vol conèixer més coses i, raonant per analogia, pensa que existeix un món més enllà del tridimensional de l’Esfera, i demana a aquesta que l’hi ensenyi: “Senyor Meu, la vostra mateixa saviesa m’ha ensenyat a aspirar a un món encara més gran, més bonic i més proper a la vostra perfecció. De la mateixa manera que vós mateix, superior a tota forma de Flatlàndia, reuniu diversos Cercles en Un, sens dubte ha d’haver-hi Algú per sobre vostre que reuneixi diverses Esferes en una Única Existència Suprema, superior fins i tot als sòlids d’Espaciolàndia. I de la mateixa manera que nosaltres, que ara som a l’Espai, ens inclinem per contemplar Flatlàndia i hi veiem l’interior de totes les coses, certament ha d’haver-hi per sobre nostre una regió més alta, més pura... un Espai encara més espaiós, una Dimensionalitat encara més dimensionable, des del cim de la qual ens inclinarem plegats sobre l’interior revelat de les coses Sòlides...”.

Però el Quadrat troba en l’Esfera una estretor mental semblant a la del rei segment de Linelàndia, i sent que li respon, de manera simplista, que una dimensió superior a la tercera només pot ser una visió generada pel pensament. Malgrat tot, el Quadrat no es dóna per vençut i, obstinat, insisteix: “Si de debò fos així, si aquest altre Espai en realitat fos Thoughtlàndia (‘el món del pensament’), aleshores porteu-me en aquesta regió beneïda... I un cop allà, voldríem frenar la marxa de la nostra ascensió? En aquella feliç regió de Quatre Dimensions, dubtaríem potser a les portes de la Cinquena i no hi entraríem?... Aleshores, cedint a l’assalt del nostre intel·lecte, les portes de la Sisena Dimensió s’obririen de bat a bat; i després, les de la Setena i la Vuitena...”.

Però aleshores el Quadrat blasfem és dipositat altre cop a Flatlàndia i abandonat al seu destí de pobre visionari, i s’acaba el llibre. Aquí es planteja al lector que s’ha rigut del caràcter obtús dels habitants de Linelàndia i de Flatlàndia, éssers inferiors, imperfectes i vacil·lants per un buit obstinat, una pregunta fatídica: com reaccionaríeu davant la revelació d’un món de dimensió diferent del vostre?

Les fractals

En els punts anteriors hem vist models geomètrics diferents, però que tenien en comú una propietat relativa a la dimensió. Precisament es tractava de models geomètrics unidimensionals com els segments, les rectes, els arcs de curvatura; o bidimensionals, com les figures planes i les superfícies de l’espai; o tridimensionals, com els sòlids; o fins i tot de més de tres dimensions, però sempre d’una dimensió entera. ¿És possible crear models geomètrics de dimensió no entera? I què en resulta? Alguns geòmetres contemporanis ho estan intentant i, gràcies a l’ajut dels ordinadors, es poden crear uns objectes bellíssims, les anomenades fractals.

El terme fractal deriva de la paraula homònima anglesa, que vol dir ‘fraccionari’, i que designa precisament figures geomètriques de dimensió no entera. Per a fer-nos una idea del que es tracta, mirarem de donar una definició nova de dimensió d’una figura geomètrica, que utilitzarem per a construir figures fractals. Per a fer-ho cal desconsiderar el sentit comú euclidià adquirit a escola i substituir-lo per una bona dosi d’imaginació. I val la pena!

Considerem, doncs, una figura geomètrica construïda així: a) Es parteix d’un segment de longitud unitària, i se subdivideix en n parts iguals, de longitud 1/n; b) En cadascuna d’aquestes parts es fa una operació de construcció geomètrica, que és precisada i que caracteritzarà la figura final. Aquesta operació s’ha de fer de tal manera que es produeixi com a primer resultat una figura constituïda per N parts iguals, cadascuna de les quals té com a base un segment de longitud 1/n, que pot no coincidir amb una de les parts del segment inicial.

Examinem ara cadascuna de les N parts; fem veure que el segment de base té una llargada unitària, i en cadascun dels N segments de base, a partir de la mateixa subdivisió en n parts, repetim la construcció anterior. Obtenim N2 parts, de la mateixa forma que les primeres N, però amb el segment de base de llargada 1/n2. Si disposéssim d’un zoom que engrandís la figura n vegades, observaríem exactament N repeticions de la figura que en el pas anterior vèiem a primer cop d’ull.

Aquest procediment es pot repetir una altra vegada, i una altra, i una altra... Amb cada repetició, la figura és formada per un nombre cada vegada més gran de parts cada cop més petites, però sempre perfectament idèntiques, quant a la forma, a la figura construïda en el primer pas. És un procediment que no s’acaba mai; si tinguéssim un bolígraf de punta finíssima i un paper finíssim arribaríem a allò infinitament petit; si tinguéssim un zoom infinitament potent ens mostraria una figura infinitament gran, però sempre perfectament semblant a ella mateixa, és a dir, una figura totes les parts de la qual són idèntiques a la figura sencera.

Considerem ara un exemple significatiu amb la construcció de l’anomenada corba de Von Koch. S’obté amb l’acoblament d’una sèrie de figures, com s’il·lustra en els dibuixos representats anteriorment: a) Tracem un segment de costat 1, i subdividim-lo en tres parts iguals, prenguem com a base el segment central, construïm-hi a sobre un triangle equilàter, i després esborrem el segment central; si tot ha anat bé en surt una línia trencada com la de la figura 1. b) Repetint el procediment s’obté la línia de la figura 2, després la de la figura 3, i així successivament.

De què serveix la geometria fractal? Mirar la figura de la corba de Von Koch que hem construït més amunt ens fa pensar en les disposicions típiques dels cristalls de glaç que formen la neu o en branques o figures vegetals. Aquests exemples ens diuen que les fractals, segons les bases teòriques definides els anys setanta pel matemàtic francès Benoît Mandelbrot, permeten descriure en termes matemàtics quantitatius estructures fortament irregulars però dotades de la propietat de l’autosemblança, que són molt comunes en la natura: un arbre, un bosc, el cim d’una muntanya, la línia de la costa, un núvol o un llamp.

La geometria fractal, doncs, cada dia s’aplica més en diverses disciplines com, sobretot, la física (distribució de les galàxies, fenòmens de turbulències o l’anomenat soroll blanc), i també la química, la biologia, la geologia o la fisiologia (perquè l’estructura del cos humà mostra molts exemples d’estructures fractals), en la mesura que permet representar nombrosíssims fenòmens que no es poden descriure en els termes de la geometria euclidiana tradicional ni en els termes habituals d’altres geometries, ja que aquests fenòmens són considerats caòtics o desordenats i per tant difícilment reduïbles a models convencionals.