L’estadística
El terme estadística suscita en molta gent un sentiment de desconfiança, ja que fa pensar en alguna cosa complicada i difícil d’entendre. Però, en realitat, l’estadística és només un conjunt d’eines que serveixen per a mesurar fenòmens col·lectius. Si volem determinar la distància entre dues ciutats, l’expressarem en quilòmetres, però per a la distància entre dues estrelles seran més adequats els anys llum; direm que una cadena d’or pesa uns grams, però la càrrega de patates d’un camió serà millor expressar-la en tones. I si hem de mesurar els productes a l’engròs o les mercaderies venudes d’un país a un altre o la renda nacional? En aquests casos, necessitarem unitats de mesura més grans i sovint més complexes, i la major part de les vegades ens caldrà l’ajut de les tècniques estadístiques per a la seva interpretació. L’estadística és aplicable a moltíssims fenòmens, com les oscil·lacions de la població, la producció agrícola, els dies de pluja i la corresponent quantitat d’aigua caiguda, la mitjana de les vendes anuals d’un producte determinat a un client per part d’una empresa i, en general, qualsevol fet variable.
L’objecte de l’estadística és l’estudi de la variabilitat d’un fenomen. La manera com dur a terme aquest estudi podrà variar, però com a resultat sempre s’obtindran nombres que descriuen els esdeveniments. El mètode estadístic no és, amb tot, una mena de màquina en la qual s’introdueixen diversos valors numèrics i en surten resultats perfectes, sinó que cal aplicar-ne els paràmetres amb intel·ligència i interpretar els resultats de manera correcta i exhaustiva.
El naixement de l’estadística
Per a trobar els orígens de l’estadística cal remuntar-se a l’Anglaterra del començament del segle XVII, encara que de molt abans era usual la recollida de dades amb fins militars, impositius o per a l’elaboració de censos poblacionals. En aquell temps, l’illa era afectada per una epidèmia de pesta, i per a saber l’extensió de la plaga es va decidir comptar cada setmana el nombre de morts causats per la malaltia a la ciutat de Londres, de manera que, en cas d’una gran proliferació del mal, se’n pogués advertir immediatament Sa Majestat, que així es podria refugiar al camp. Els compiladors dels registres de mortalitat es limitaven a considerar el total de defuncions, sense preguntar-se quina era la causa de la mort, mentre que per a saber el nombre de naixements consultaven els registres de les parròquies, bé que no tots els nens eren batejats —per tant, les dades no eren del tot fiables—. Això no obstant, un tal John Graunt, comerciant de teixits de professió, va aconseguir fer un càlcul de la població de Londres basant-se en les dades de què disposava. El mètode que va seguir és el primer exemple històric del mètode estadístic. Vegem en què consisteix.
Graunt sabia el nombre anual dels naixements, i d’aquest nombre en va deduir el de les dones en edat fèrtil. Va calcular que, com que les dones en aquella època tenien un fill cada dos anys de mitjana, el nombre de dones en edat fèrtil era el doble que el de naixements, i que el nombre total de dones era el doble que el de les dones en edat fèrtil. A més, Graunt tenia una idea ben precisa de com era la família tipus de l’època, que va suposar formada per vuit membres (inclosa la figura central de la dona esposa i mare); amb aquestes dades, només calia fer una sèrie de multiplicacions, partint del nombre de naixements en un any, que era de 12 000:
12 000 (naixements) x 2 = 24 000 dones en edat fèrtil
24 000 (dones en edat fèrtil) x 2 = 48 000 dones en total
48 000 (dones en total) x 8 = 384 000 habitants en total.
Sens dubte, aquest càlcul presenta errors, però és una mostra clara de com Graunt va interpretar les dades de què disposava; aquesta interpretació de dades és el començament del que anomenem estadística.
Com es fa un estudi estadístic
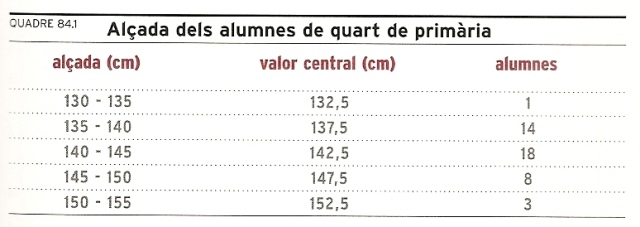
Quadre 84.1 Alçada dels alumnes de quart de primària.
ECSA
Suposem que volem saber l’alçada dels alumnes d’una classe de quart curs de primària d’una escola. Una primera idea podria ser mesurar tots els alumnes de la classe i passar les mesures obtingudes a una taula. Però si algú ens preguntés quina és bàsicament l’alçada dels alumnes, no tindria gaire sentit ensenyar-li la llista de les mesures, perquè seria una resposta llarga i confusa. És molt millor respondre amb un nombre que sintetitzi les dades que hem reunit. Aquest nombre és la mitjana aritmètica, és a dir, la suma de totes les alçades mesurades dividida pel nombre dels alumnes de la classe.
Si ara volguéssim saber l’alçada dels alumnes de totes les classes de quart de l’escola (suposant que aquesta no fos gaire gran), podríem tornar a mesurar els alumnes un per un, però ens adonaríem que la diversitat de les mesures obtingudes fa massa complicada l’operació de traslladar les dades a una taula. Per això convé agrupar les alçades en blocs (o classes); per exemple, prenent les mesures en centímetres, les classes podrien ser de 130 a 135, de 135 a 140, de 140 a 145, i així successivament. Per a facilitar la manipulació posterior d’aquestes dades, és interessant determinar els valors centrals de cada classe, en aquest cas: 132,5; 137,5; 142,5; etc. Amb l’ordenació en classes s’obté una sèrie discontínua de dades que modifica una mica el fenomen, però que en simplifica molt l’estudi. I si al costat de cada classe s’escriu el nombre d’individus que la constitueixen —posant de manifest, doncs, la freqüència—, s’obtindrà encara una millor descripció del fenomen. Així, podrem constatar que els valors extrems corresponen a pocs individus, mentre que els valors intermedis són ocupats per un nombre cada vegada més gran d’individus a mesura que ens acostem a la classe que n’inclou el nombre més gran, que s’anomena moda o valor modal de l’observació més freqüent. En l’exemple del quadre 84.1, “Alçada dels alumnes de quart de primària”, el valor modal o moda és 142,5 cm. L’alçada mitjana de tots els alumnes de quart de primària s’obtindrà sumant els productes de cada freqüència pel valor central de la classe corresponent i dividint aquesta suma pel nombre d’alumnes.
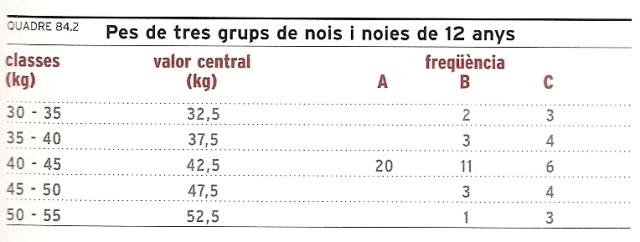
Quadre 84.2 Pes de tres grups de nois i noies de 12 anys.
ECSA
Engrescats amb aquests resultats, ara volem mesurar l’alçada de tots els alumnes de l’escola. Però, com que en són massa, no es podran examinar tots els individus un per un; per tant, serà convenient prendre en consideració una mostra, això és, un grup elegit del conjunt de tots els individus que es vol estudiar. És molt important que aquesta mostra reflecteixi totes les característiques essencials del conjunt de partida; és a dir, que sigui una mostra representativa. Per a fer-ho bé cal que la mostra triada tingui una dimensió adequada i, a més, que sigui seleccionada de manera del tot aleatòria. Pel que fa a l’aleatorietat, el problema es resol fàcilment fent un sorteig entre tots els individus del conjunt que s’examina. Quant a les dimensions, el nombre dels participants en el sorteig es determina segons el criteri del qui fa l’estudi. Òbviament, com més alt sigui el nombre de persones examinades, més representativa en serà la mostra, però més cara i feixuga en serà l’anàlisi. Per això, és oportú triar una mostra representativa que no sigui ni gaire escassa ni gaire nombrosa. Les tècniques de la teoria del mostreig estadístic garanteixen la representativitat de les mostres i el tractament matemàtic de les dades. Així, un cop establerta la mostra, se’n fan les mesures relatives al fenomen que s’estudia —en aquest cas les alçades dels alumnes de tota l’escola— i es recullen les dades en una taula, com hem fet abans.
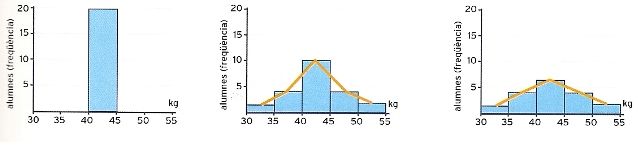
Representació en histogrames de les dades del quadre 84.2.
ECSA
mateix procediment se segueix tant si es vol mesurar l’alçada dels escolars, com el diàmetre dels ous d’una granja de gallines o qualsevol altre fet d’aquest tipus. La mitjana aritmètica i la freqüència ens donen una idea, bé que imprecisa, de la variació del fenomen.
Però hi ha nombrosos fenòmens dels quals resulta molt interessant estudiar no solament la variació, sinó també la manera com es produeix aquesta variació. Suposem, per exemple, que tenim tres grups de vint nois i noies, d’uns 12 anys, dels quals sabem la distribució segons el pes. Als tres grups A, B, C la distribució és la indicada en el quadre 84.2, “Pes de tres grups de nois i noies de 12 anys”. Les mitjanes dels pesos dels tres grups són de 42,5, 42 i 42,5 kg respectivament. Però si observem la taula ens adonem que, encara que els pesos mitjans siguin gairebé iguals, la composició de cada grup és ben diferent. En el primer cas, tots els nois tenen aproximadament el mateix pes, perquè entren tots en la mateixa classe (40-45); per això es diu que la variabilitat del fenomen, és a dir, la dispersió al voltant de la mitjana, és nul·la. En el segon cas, els pesos són més diferenciats, però es concentren al voltant del valor mitjà, i per això diem que la variabilitat és baixa. En el tercer cas, la dispersió dels pesos respecte del valor mitjà és més gran (hi ha més nois prims i més nois grassonets), i aleshores diem que la variabilitat del fenomen és alta.
El paràmetre que mesura la variabilitat s’anomena variància, i és expressat per la fórmula següent:
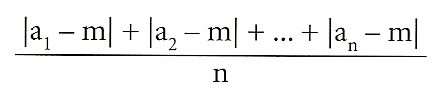
en què a1, a2, ... an són les dades obtingudes, m és la mitjana aritmètica d’aquests valors i n és el nombre d’individus examinats. Hem vist, doncs, que uns pocs paràmetres fonamentals, com la mitjana i la variància (o bé la desviació típica o estàndard, que és l’arrel quadrada de la variància), descriuen un fenomen de manera prou satisfactòria. Naturalment, per a una anàlisi més aprofundida caldrien altres paràmetres. De totes maneres, és evident que una de les característiques principals de l’estadística és la seva gran capacitat de síntesi.
Errors en la utilització de l’estadística
L’ús del mètode estadístic pot generar diferents errors. Es pot cometre un primer error en l’elecció de la mostra. Suposem, per exemple, que una empresa vol llançar un nou producte al mercat i, per tant, vol tenir una idea de l’acceptació que tindrà. Imaginem-nos que es tracta d’una sopa instantània, un d’aquells productes als quals només cal afegir aigua bullent per a obtenir, després de remenar-ho una mica, un primer plat saborós i fumejant. Si el sondeig es fa entre els treballadors d’una gran empresa, triats a l’atzar, les respostes no donaran un resultat significatiu, perquè el percentatge de respostes favorables probablement serà superior al que s’obtindria enquestant tota la població. En efecte, la mostra elegida és formada per persones que passen bona part del dia fora de casa i, per tant, aprecien un producte que es pugui cuinar ràpidament (vegeu “Els sondeigs d’opinió”).
Un altre tipus d’error que es pot cometre és la mala interpretació de les dades estadístiques. Imaginem-nos que tenim dues classes paral·leles de la mateixa escola. A la primera classe, els alumnes que a la primera avaluació han aprovat el llatí són el 48%, mentre que a la segona classe són el 12%. Al cap d’un període de recuperació, els aprovats assoleixen el 51% i el 15% respectivament. Aparentment, hi ha la mateixa millora del 3% a totes dues classes, però, si comparem l’augment dels aprovats amb el percentatge anterior, veiem que la millora de la primera classe és del (51 - 48)/48 = 0,06%, mentre que la de la segona és del (15 - 12)/12 = 0,25%.
Representació gràfica de les estadístiques
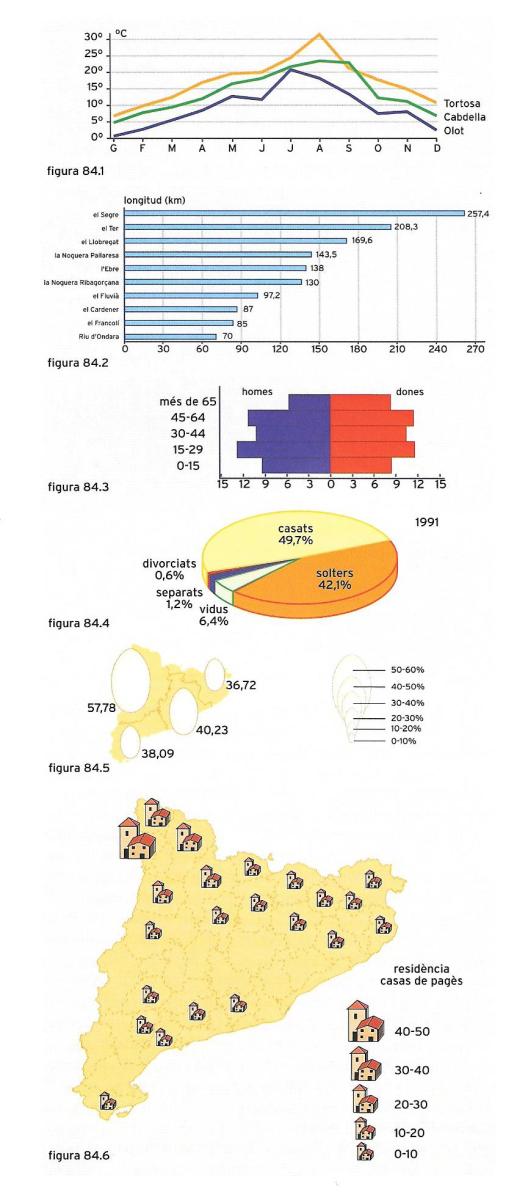
Sis maneres de representar les dades estadístiques (vegeu-ne els detalls en el text): 1. Gràfic lineal compost; 2. Diagrama de barres; 3. Piràmide estadística; 4. Diagrama de sectors; 5. Pictograma; 6. Cartograma.
ECSA
Si bé les dades estadístiques es recullen en taules abans de ser interpretades, com hem vist, una llarga llista de nombres no dóna una idea immediata del funcionament d’un fenomen determinat. Sovint convé expressar les dades numèriques per mitjà de gràfics, formats per punts, línies i figures geomètriques que es mostren a la vista amb una claredat que les xifres no solen tenir i que són comprensibles fins i tot pels profans. Els sistemes utilitzats per a la representació gràfica de les dades són molts, i la tria depèn de diferents elements, com el tipus de dades, el grau de precisió desitjada, l’ús que se’n vol fer i el públic al qual es destina el gràfic. A continuació es descriuen alguns dels mètodes de representació més emprats, com són el sistema de coordenades rectangulars amb gràfics lineals simples o compostos, el diagrama de barres, l’histograma i la piràmide, el diagrama de sectors, el pictograma i el cartograma.
El sistema de coordenades rectangulars o cartesianes, introduït ja per Descartes l’any 1637, resulta utilíssim per a estudiar l’evolució d’un fenomen a través del temps. Es tracen dos eixos perpendiculars entre ells i una escala per a les unitats de mesura. A l’eix horitzontal (o eix d’abscisses) se solen situar les dades temporals, i al vertical (o eix d’ordenades), les dades obtingudes. Per exemple, en la figura 84.1 es representen les temperatures mitjanes mensuals d’un any de tres poblacions catalanes. L’anotació de les diferents temperatures forma un diagrama de punts, els quals es poden unir per una línia trencada per a facilitar-ne la lectura; es tracta llavors d’un gràfic lineal, que pot ser simple, si hi ha una sola representació, o bé compost, si inclou representacions diverses (com és el cas de l’exemple de la figura 84.1).
El diagrama de barres fa servir també un eix de coordenades cartesianes, on la intensitat del fenomen observat determina la longitud o l’altura del traç; en certa manera, permet la representació a escala de les dades. És un gràfic que s’utilitza quan es vol posar en relleu les diferències que existeixen entre els valors d’una taula, com per exemple les longituds dels principals rius catalans (figura 84.2).
L’histograma és una representació en dues o tres dimensions, construït amb rectangles de bases adjacents, molt usual quan es disposa d’una variable estadística contínua (els valors de la variable s’agrupen en els anomenats intervals de classe). A l’eix horitzontal es col·loquen els valors de la variable, ordenats en classes, i al vertical, les freqüències. Per exemple, les dades del quadre 84.2 es representen en els histogrames corresponents. L’histograma es traça quan té un significat la suma dels valors de cada classe, ja que l’àrea total de cada rectangle es correspon amb el total dels valors de la classe representada. Els punts centrals dels sostres dels rectangles es poden unir per mitjà d’una línia a fi d’obtenir un polígon de freqüències.
Una variació interessant dels histogrames són les piràmides, representacions estadístiques que es fan servir principalment per a presentar dades poblacionals (vegeu la figura 84.3); són gràfics que consten bàsicament de dos histogrames adossats per la base, que ofereixen la comparació visual de dos sistemes de dades.
Els diagrames de sectors, que popularment anomenem formatges o gràfics en pastís, consisteixen en un cercle en el qual es tracen diferents sectors circulars que representen gràficament els valors en percentatge. Posen de manifest una certa part respecte del conjunt. Per exemple, si volem mostrar les dades relatives als percentatges de l’estat civil de la població catalana, tindrem el diagrama de la figura 84.4. La construcció d’aquests diagrames es realitza dividint la superfície total del cercle en sectors proporcionals a la intensitat del fenomen estudiat i indicant-ne els percentatges en els diferents sectors considerats.
Els pictogrames són gràfics estadístics en què s’empra la imatge del fenomen que es vol representar. Aquesta imatge o símbol corresponent a la magnitud considerada es pren com a unitat de mesura. Tant es pot utilitzar la mateixa imatge repetida un cert nombre de vegades, com una imatge representada en diferents dimensions per a mostrar els valors respectius de les dades, com en la figura 84.5, que representa el consum mitjà diari d’ous per persona (la mitjana catalana del qual és 40,81 grams bruts per persona/dia); de tota manera, sovint aquestes figures solen anar acompanyades de les xifres dels valors corresponents a la intensitat dels fenòmens descrits. Els pictogrames són molt atractius visualment perquè permeten una visió gràfica immediata del fenomen estudiat, però són menys exactes que altres sistemes de representació estadística.
Finalment, els cartogrames són representacions gràfiques utilitzades per a descriure un fenomen, i de vegades també la seva evolució, en un determinat territori, com podria ser la densitat de població, les precipitacions anuals o el nombre i la distribució comarcal de les residències-casa de pagès catalanes (vegeu la figura 84.6). Sovint es tracta d’elaboracions estadístiques per mitjà de figures proporcionals localitzades en un mapa o sobre un fons cartogràfic adequat.
El càlcul de probabilitats
Quan es discuteix sobre probabilitats, sempre es parla d’esdeveniments o fets. Uns fets que es poden produir o no. Hi ha fets certs, que són els que s’esdevindran amb seguretat; fets impossibles, que no s’esdevindran mai, i fets probables, que poden succeir o no. Precisament, l’ocurrència o la no-ocurrència dels fets probables depèn exclusivament de l’atzar, és a dir, d’un conjunt de causes desconegudes l’acció combinada de les quals pot influir en el fet en qüestió. Tot i això, convé tenir en compte que un fet pot ser casual si es considera un cert nombre de circumstàncies, però pot esdevenir completament determinat si se’n pren un conjunt molt més ampli. Així, en teoria, el fenomen físic consistent en el llançament d’una moneda és determinat per les lleis de la mecànica (la mecànica és la branca de la física que estudia, en general, el moviment), fins al punt que es pot preveure si sortirà cara o creu; en la pràctica, però, les mínimes variacions de les nombroses magnituds físiques que hi intervenen fan impossible preveure el resultat d’un llançament. Per això, hem de saber que la probabilitat d’un esdeveniment és la relació entre el nombre de casos favorables a la verificació del fet mateix i el nombre de casos possibles; per tant, és un valor que va del 0 (quan el fet és impossible) a l’1 (quan el fet és cert).
La probabilitat d’un esdeveniment
Si volem calcular la probabilitat que ens surti cara en llançar una moneda, tindrem un cas favorable de cada dos de possibles; la probabilitat, per tant, serà de 0,5 (o del 50%). Si volem determinar la probabilitat que surti un 6 tirant el dau una sola vegada, veurem que és d’1/6, perquè només hi ha un cas favorable entre sis casos possibles. Però, naturalment, les coses no sempre són tan elementals.
Per exemple, podríem preguntar-nos quina és la probabilitat que dels tres fills d’una família hi hagi dos nens (N) i una nena (n), donant per bo que el naixement d’un nen o una nena són igualment probables. De primer, veiem que hi ha aquests vuit casos possibles:
N-N-N n-N-N
N-N-n n-N-n
N-n-N n-n-N
N-n-n n-n-n
D’aquests vuit casos, només tres són favorables (que hem indicat en cursiva); així, la probabilitat és de 3/8. A partir de l’anàlisi de l’esquema, és fàcil comprendre quina és la probabilitat que la família tingui, per exemple, dues nenes i un nen (3/8), tres nenes (1/8) o tres nens (1/8).
Determinem ara la probabilitat de fer un ple al popular joc de la primitiva o de la 6/49. En aquest joc, el premi màxim consisteix a endevinar els sis nombres extrets de la sèrie de l’1 al 49 (en aquest exemple no tindrem en compte els premis menors ni els reintegraments). Els casos possibles, doncs, són totes les combinacions de sis elements que es poden formar amb 49 nombres. Determinar quines són aquestes combinacions amb un diagrama com l’anterior seria massa llarg; per sort, les matemàtiques ens proporcionen la fórmula per a calcular-ne el nombre, que en aquest cas és de 13 983 816. Aquesta xifra ha estat obtinguda en aplicar la fórmula general:
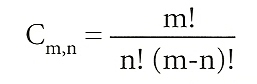
En aquesta fórmula, m és el nombre d’elements considerats de n en n; i el signe “!” indica la factorial (producte dels nombres consecutius des de l’1 fins al nombre considerat); en el nostre cas, m = 49 i n = 6, de manera que, segons la fórmula suara esmentada:

Com que hi ha, doncs, gairebé 14 milions de combinacions possibles, la probabilitat de fer un ple de sis encerts és veritablement esquifida: 1/ 13 983 816 = 0,0000000715 o, el que és el mateix 7,15 · 10-8. A aquest mateix resultat arribaríem també considerant els casos probables entre els casos possibles per a cadascun dels sis nombres de la combinació guanyadora, i aplicant la fórmula de la probabilitat total, és a dir:
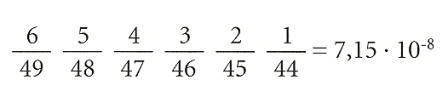
Els sondeigs d’opinió
El terme sondeig indica un estudi estadístic, basat en l’anàlisi d’una mostra representativa de la població que es pretén estudiar. El sondeig d’opinió, en particular, s’utilitza per a saber l’orientació de l’opinió pública o de determinats grups socials sobre qüestions polítiques, socials, econòmiques, etc. El sondeig d’opinió més conegut és el que preveu els resultats d’unes eleccions.
El sondeig d’opinió va néixer als Estats Units d’Amèrica els anys trenta per obra de George Gallup, i durant les últimes dècades s’ha difós àmpliament en altres països. Es realitza plantejant preguntes prefixades a cada individu de la mostra desitjada i recollint-ne les respostes; les preguntes les pot fer un entrevistador directament o per telèfon, o bé es poden plantejar per correu o per qualsevol altre sistema. A l’hora de formular-les, s’utilitzen diverses tècniques, suggerides per l’experiència i motivades principalment per consideracions d’ordre psicològic, per tal de no influir en els entrevistats i obtenir-ne respostes clares.
Són tècnicament anàlegs als sondeigs d’opinió els sondeigs de mercat, també anomenats anàlisis o recerques o enquestes de mercat. Els sondeigs de mercat, relatius als problemes de distribució i venda de serveis o de béns de consum, en general es proposen arribar a una valoració d’un o més dels aspectes següents del mercat: a) la quantitat dels diversos productes consumits en una unitat de temps donada; b) el nombre d’individus interessats en la compra d’un bé determinat; c) les preferències dels consumidors per determinades marques, confeccions, empreses de venda i de distribució; d) les àrees de venda dels diversos centres comercials, és a dir, les zones territorials al voltant d’aquests centres els habitants de les quals hi van a comprar, i e) l’eficàcia de les diverses tècniques publicitàries.
Esdeveniments simultanis i probabilitat total
Fins ara hem examinat la possibilitat que es produeixi un sol fet cada vegada, però també pot donar-se el cas que dos o més esdeveniments es produeixin simultàniament. Suposem que tenim dues bossetes, en la primera de les quals hi ha 20 boles vermelles i 80 de blanques, mentre que la segona conté 30 boles vermelles i 70 de blanques. Quina és la probabilitat que en treure una bola de cada bosseta siguin totes dues vermelles?
En primer lloc, cal saber quants són els casos possibles. Com que, independentment del color, cada bola de la primera bosseta es pot combinar amb una de la segona, hi haurà 100 x 100 = 10 000 casos possibles. Perquè ens surtin un parell de boles vermelles, una de cada bossa, observem que cadascuna de les 20 boles vermelles de la primera bossa es pot combinar amb cadascuna de les 30 de la segona. Per això, els casos favorables són 20 x 30 = 60. La probabilitat que volíem determinar serà, per tant:
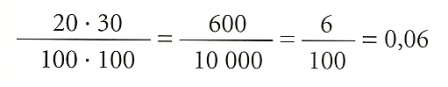
Com es pot veure, la probabilitat total no és sinó el producte de les probabilitats parcials: 20/100 i 30/100. Per tant, és evident que el fet d’afegir condicions pot modificar la probabilitat d’un esdeveniment i que el càlcul no sempre és senzill.
Probabilitat subjectiva
Quan els fets no són tots igualment possibles, la definició de probabilitat que hem donat abans ja no és l’adequada. Suposem que assistim a un partit de tennis. La probabilitat que guanyi un dels dos jugadors ja no és de 0,5 com passava amb la probabilitat que sortís cara o creu en el llançament d’una moneda. En efecte, un dels dos tennistes pot estar més ben preparat o trobar-se en millor forma; per això, les probabilitats de guanyar no són les mateixes per a tots dos. En casos com aquests, es parla de probabilitat subjectiva, que es defineix com que un fet té A/100 probabilitats de succeir si donem per bo pagar A per obtenir 100 en el cas que el fet es produeixi. En el cas d’esdeveniments igualment probables, aquesta definició i la del paràgraf anterior coincideixen.
La probabilitat i els jocs d’atzar
Encara que de vegades no ho sembli, el càlcul de probabilitats s’utilitza moltíssim en la vida quotidiana. Hi recorre el polític per a planificar la seva campanya electoral, el botiguer per a comprar les seves provisions o el pagès per a preveure’n la collita.
Però la teoria de la probabilitat es remunta a més de tres-cents anys enrere, com a mètode per a resoldre problemes dels jocs d’atzar (vegeu “La teoria de la probabilitat”).
Suposem que dos amics llancen una moneda per veure si surt cara o creu. Tots dos tenen les mateixes probabilitats de guanyar (1/2 o 0,5 o el 50%). Ara bé, si en un joc qualsevol la probabilitat és inferior a 0,5, és millor anar amb compte. Suposem que qui fa de banca planteja la juguesca de pagar el que s’hagi apostat en cas de treure com a mínim un 6 en tirar un dau quatre vegades. És convenient per al jugador acceptar l’aposta?
Examinem quina probabilitat té la banca de guanyar (o de perdre). En la primera tirada la probabilitat que no li surti el 6 és de 5/6, la mateixa que en les tirades següents. La seva probabilitat, doncs, de perdre l’aposta és 5/6 x 5/6 x 5/6 x 5/6 = 0,482. El complementari d’aquest nombre serà la probabilitat que té la banca de guanyar, és a dir: 1 - 0,482, o sigui, 0,518. Consegüentment, si la banca aposta que traurà un 6 almenys en una de les quatre tirades, és més prudent no acceptar l’aposta, perquè el jugador partiria amb un desavantatge, atès que el guany no és proporcional al risc.
La teoria de la probabilitat
La teoria de la probabilitat o càlcul de probabilitats va néixer a partir de l’estudi d’alguns problemes relatius als jocs d’atzar. Luca Pacioli, autor del primer tractat general d’aritmètica i d’àlgebra, cap al final del segle XV; Gerolamo Cardano, matemàtic, metge i autor de Liber de ludo alea, on presenta el primer càlcul sistemàtic de probabilitats, de mitjan segle XVI, i fins i tot Galileu, al final d’aquell segle, ja van fer recerques importants en aquest camp.
Amb tot, el problema històricament més famós és el que, el 1654, va plantejar al matemàtic, físic i filòsof francès Blaise Pascal un jugador empedreït, el cavaller de Meré, que volia saber per què en tirades de tres daus la suma 11 era més freqüent que la suma 12, encara que totes dues sumes poden obtenir-se de sis maneres diferents i, per tant, haurien de tenir la mateixa probabilitat. Pascal, un cop va haver demostrat matemàticament el problema de Meré (és cert que la probabilitat d’obtenir la suma 11 és lleugerament superior a la de la suma 12), va romandre vivament interessat en el nou tema d’estudi, i va comunicar les seves idees a Pierre Fermat, amb qui va mantenir una densa correspondència relativa a alguns problemes del nou càlcul.
Les primeres exposicions de la teoria de la probabilitat, que mentrestant havia començat a desvincular-se del camp limitat als jocs d’atzar, es deuen al físic neerlandès Christiaan Huygens i al matemàtic suís Johann Bernoulli, que va demostrar entre altres coses el teorema fonamental que porta el seu nom i que relaciona la freqüència amb la probabilitat, la qual esdevé el valor mitjà de la freqüència quan es realitza un nombre molt gran de proves. Al segle XVIII, la teoria de la probabilitat, malgrat els seus continus progressos i les útils aplicacions a la demografia i les assegurances, encara no gaudia d’una consideració seriosa entre els qui es dedicaven a les ciències naturals, que tenien idees confuses sobre la naturalesa del nou càlcul. No va ser fins a l’aparició de les obres fonamentals de Pierre Laplace, en especial la Théorie analytique des probabilités (1812), que la teoria de la probabilitat va assolir un cert reconeixement i va poder entrar per la porta gran dins l’àmbit de les ciències naturals.
Encara avui, els estudiosos tenen punts de vista molt diferents sobre el significat del terme probabilitat. Les raons d’aquestes divergències es poden trobar, almenys en part, en els canals a través dels quals han sorgit els diversos conceptes científics de probabilitat (estudi de problemes inherents als jocs d’atzar, a les assegurances, al càlcul dels errors, a les ciències socials o a la física de les partícules). A grans trets, se sol distingir tres interpretacions del concepte de probabilitat: la concepció clàssica, la freqüentista i la subjectivista.
Segons la concepció clàssica, representada per Laplace, la probabilitat d’un fet és la relació entre el nombre dels casos favorables a la verificació del fet i el nombre dels casos possibles, en la hipòtesi que aquests siguin tots igualment probables. Aquesta definició, que va ser la més acceptada des del segle XVII fins al XIX, és motivada per l’examen d’aquells jocs d’atzar en el mecanisme dels quals es pot trobar una propietat de simetria, almenys idealment.
En la concepció freqüentista, propugnada per Richard von Mises i Hans Reichenbach, la probabilitat d’un esdeveniment es defineix com el límit, que se suposa que existeix, a què tendeix la freqüència relativa del fet en una successió casual de proves repetides. Per freqüència relativa, o simplement freqüència, s’entén la relació entre el nombre de vegades que es produeix el fet i el nombre total de proves considerades. Si llancem diverses vegades una moneda, encara que tinguem la màxima cura perquè les condicions en què es repeteix l’experiment es mantinguin tan constants com sigui possible, no es pot preveure amb certesa si en un llançament determinat de la moneda s’obtindrà cara o creu. Amb tot, fent una llarga sèrie de llançaments, s’observa el fenomen de la regularitat estadística, és a dir, la freqüència de l’esdeveniment ‘sortir cara’ s’estabilitza al voltant d’un valor determinat.
Finalment, per a la concepció subjectivista (lligada, amb matisos, als noms de John Keynes, Frank Ramsey, B. de Finetti i L.J. Savage), la probabilitat d’un fet és la mesura del grau de confiança que un individu atribueix a la seva verificació. En aquest ordre d’idees, la probabilitat d’un esdeveniment es pot definir com la relació entre la quantitat que l’individu en concret està disposat a arriscar i la que rebria en cas que el fet es produís.
L’esperança matemàtica
Suposem que una persona paga cada mes la quantitat de 10 000 pessetes per una assegurança de vida de 2 milions. Si al cap d’un any encara és viva, la companyia haurà obtingut 120 000 pessetes, però, si es mor, haurà pagat 2 milions, amb una pèrdua neta d’1 880 000 pessetes.
Naturalment, les probabilitats de mort augmenten a mesura que es fan anys, i les companyies d’assegurances han elaborat taules de mortalitat en què es recullen les probabilitats de mort en cada franja d’edat. Per exemple, la probabilitat de morir d’una persona de 40 anys és de 0,0098; per això, si la companyia assegura 100 persones de 40 anys amb la pòlissa anterior, guanyarà 12 milions, i se’n gastarà 0,0098 x 100 x 2 000 000, és a dir, 1 960 000. La diferència entre els ingressos i la despesa prevista és la quantitat de què la companyia pot disposar per a les seves despeses i els seus beneficis. El producte de la probabilitat d’un fet pel valor atribuït a la seva ocurrència s’anomena esperança matemàtica. La loteria ens pot facilitar un exemple senzill. Si el premi és de 10 000 pessetes i la probabilitat de guanyar és d’1 sobre 100, l’esperança de guanyar és: 10 000 x 1/100 = 100. Llavors, si el bitllet costa més de 100 pessetes, comprar-ne un significa programar perdre els nostres diners.
En una màquina escurabutxaques, la probabilitat de guanyar se situa pels volts de 0,4 (sobre el 40%, doncs). Si posem 100 pessetes a la màquina, l’esperança matemàtica és de 100 x 0,4 = 40. Això vol dir que, de cada 100 pessetes introduïdes a la màquina, podem esperar guanyar-ne 40. Es tracta, doncs, d’un entreteniment força car. D’altra banda, els reglaments de les apostes i dels jocs d’atzar solen preveure que la part afavorida sigui sempre l’organitzador del joc.